Harmonics

Bozeman Science
5 Jun 201508:29
EducationalLearning
32 Likes 10 Comments

TLDRIn this AP Physics essentials video, Mr. Andersen explores the concept of harmonics, focusing on their relationship with the fundamental frequency. Using the guitar as a practical example, he explains how frets correspond to different harmonics and how standing waves create these frequencies. The video delves into calculating the wavelength and frequency of harmonics, emphasizing the inverse relationship between wavelength and frequency. Through a simulation, viewers learn to identify harmonics and perform calculations for different scenarios, gaining a solid understanding of harmonics in physics.

Takeaways
  • ๐ŸŽธ Harmonics are integer multiples of the fundamental frequency, which is the frequency when a string vibrates over its entire length.
  • ๐Ÿ“ The twelfth fret on a guitar is significant because it is halfway along the string, relating to the second harmonic.
  • ๐ŸŒŠ Standing waves are created by the interference of waves, resulting in waves that appear to be stationary.
  • ๐Ÿ”„ The wavelength of a fundamental frequency is twice the length of the boundary (like the length of a string).
  • ๐ŸŒ€ The frequency of a wave is the velocity of the wave divided by its wavelength, and velocity is the frequency times the wavelength.
  • ๐Ÿ“ˆ As you move up in harmonics, the wavelength becomes shorter and the frequency increases.
  • ๐ŸŽป Guitarists can play harmonics by briefly touching the twelfth fret, producing multiple frequencies thatๅ ๅŠ  (superpose) on each other.
  • ๐Ÿ“ For a given boundary length L, the fundamental frequency fits half a wavelength inside the boundary.
  • ๐Ÿ”ข The second harmonic has a wavelength equal to the length of the boundary, and each subsequent harmonic's wavelength is a fraction of the boundary length.
  • ๐Ÿงฎ To calculate the frequency of a harmonic, use the formula frequency = velocity / wavelength, and adjust for the specific harmonic's wavelength.
  • ๐Ÿšฆ The period of a wave is the reciprocal of its frequency, which decreases as the frequency increases with higher harmonics.
Q & A

  • What are harmonics in the context of the video?

    -Harmonics are integers of the fundamental frequency, which relate to the overtones produced in a vibrating system such as a musical instrument string.

  • How is the twelfth fret on a guitar related to harmonics?

    -The twelfth fret on a guitar is significant because it is the halfway point of the string, which corresponds to the second harmonic where the wavelength fits exactly within the length of the string.

  • What are standing waves and how are they created?

    -Standing waves are waves that appear to not move and are created by the interference of waves reflecting back and forth between two boundaries, such as the ends of a string.

  • How does the wavelength of a standing wave relate to the boundary length?

    -The wavelength of a standing wave is determined by the boundary length and the mode of vibration. For the fundamental frequency (first harmonic), the wavelength is twice the length of the boundary.

  • What is the relationship between frequency, wavelength, and wave velocity?

    -The frequency of a wave is the velocity of the wave divided by its wavelength. In other words, velocity equals frequency times wavelength.

  • How does the frequency change as you move up in harmonics?

    -As you move up in harmonics, the wavelength becomes shorter, and as a result, the frequency increases.

  • What is the fundamental frequency in terms of the string length?

    -The fundamental frequency corresponds to the first harmonic where half of the string's length vibrates as a single wavelength.

  • How can you calculate the frequency of a harmonic?

    -To calculate the frequency of a harmonic, you divide the wave velocity by the wavelength of that harmonic.

  • What happens to the period of a wave as the frequency changes?

    -The period of a wave is the reciprocal of its frequency. Therefore, as the frequency increases, the period decreases.

  • How does the second harmonic differ from the first in terms of wavelength and nodes?

    -The second harmonic has a wavelength equal to the length of the boundary, and it features a node at each end, unlike the first harmonic which has a half-wavelength fitting into the boundary.

  • What is the significance of understanding harmonics in physics?

    -Understanding harmonics is crucial for analyzing sound production in musical instruments, acoustics, and wave behavior in various physical systems.

Outlines
00:00
๐ŸŽธ Introduction to Harmonics and the Guitar Example

This paragraph introduces the concept of harmonics as integers of the fundamental frequency, using the example of a guitar to illustrate. Mr. Andersen explains that the fundamental frequency is the vibration of a string at its full length, creating standing waves. The twelfth fret on a guitar is highlighted as a significant point where the string's length is halved, corresponding to the second harmonic. The paragraph discusses how standing waves are formed due to wave interference and how the wavelength is determined by the boundary conditions and frequency, with the fundamental frequency's wavelength being twice the length of the string.

05:02
๐Ÿ“ Calculating Wavelength and Frequency for Harmonics

In this paragraph, the process of calculating the wavelength and frequency for different harmonics is detailed. It explains how the wavelength of the first harmonic is twice the length of the boundary, while subsequent harmonics have wavelengths equal to the boundary length and two-thirds the length, respectively. The relationship between wavelength and frequency is discussed, noting that as wavelength decreases, frequency increases. A practical example is given where a 2-meter long string is used to demonstrate the calculation of wavelength for the first and second harmonics, emphasizing the inverse relationship between wavelength and frequency.

Mindmap
Keywords
๐Ÿ’กHarmonics
Harmonics are integer multiples of the fundamental frequency, which is the lowest frequency of a periodic wave. In the context of the video, this concept is illustrated through the example of a guitar, where plucking a string at different frets produces harmonics that are integer multiples of the fundamental frequency determined by the string's length. The video explains how these harmonics create standing waves, which are essential for understanding the behavior of sound and vibrations in various musical instruments.
๐Ÿ’กFundamental Frequency
The fundamental frequency is the basic frequency of a periodic wave, often associated with the lowest pitch of a sound. In the video, it is demonstrated by plucking a guitar string and observing the whole length vibrating, which produces the fundamental frequency. This frequency is the starting point for understanding harmonics, as all other harmonics are integer multiples of this basic frequency.
๐Ÿ’กStanding Waves
Standing waves are waves that appear to be stationary due to the interference of waves reflecting back and forth between two points. In the video, standing waves are created when the vibrations of a string, like a guitar string, interfere with themselves, leading to a pattern of nodes and antinodes. These standing waves are crucial for understanding how harmonics are formed and how they contribute to the overall sound produced by an instrument.
๐Ÿ’กNodes
Nodes are points on a standing wave where there is no displacement; in other words, they are points of zero amplitude. The video uses the example of the second harmonic on a guitar, where there are nodes at the ends and a node in the middle. Nodes are significant in the study of harmonics because they indicate points of minimal vibration, which is essential for understanding the pattern of a standing wave.
๐Ÿ’กWavelength
Wavelength is the distance between two consecutive points in phase, such as two crests or two troughs of a wave. In the video, the wavelength is determined by the boundary conditions, such as the length of the string on a guitar. The relationship between wavelength and frequency is fundamental to understanding how different harmonics are produced and how they affect the sound of an instrument.
๐Ÿ’กFrequency
Frequency refers to the number of complete cycles of a wave that occur in a unit of time, typically measured in Hertz (Hz). In the context of the video, frequency is related to how fast the string vibrates, which in turn affects the pitch of the sound produced. The video explains how the fundamental frequency and its harmonics can be calculated based on the wavelength and the speed of the wave in the string.
๐Ÿ’กVelocity
Velocity in the context of wave motion is the speed at which the wave propagates through a medium. The video explains that the frequency of a wave is related to its velocity and wavelength by the equation frequency equals velocity divided by wavelength. This relationship is crucial for calculating the frequencies of the harmonics on a stringed instrument like a guitar.
๐Ÿ’กInterference
Interference is a phenomenon that occurs when two waves meet and combine, resulting in a new wave pattern. In the video, interference is responsible for the creation of standing waves, which is essential for the formation of harmonics. The constructive and destructive interference of the waves leads to the formation of nodes and antinodes, which are characteristic features of standing waves and harmonics.
๐Ÿ’กGuitar Frets
Guitar frets are the metal strips on the neck of a guitar that divide the fingerboard into sections. When a string is pressed down against a fret, it is shortened, changing the length of the vibrating portion and thus altering the pitch. The video uses the example of the twelfth fret, which is halfway along the guitar's neck, to illustrate how harmonics can be produced at specific points along the string, contributing to the rich sound of a guitar.
๐Ÿ’กSimbucket Simulation
The Simbucket Simulation mentioned in the video is a tool used to visually demonstrate the principles of wave motion, including harmonics and standing waves. By using this simulation, the video aims to provide a practical and interactive way for viewers to understand how changing the wavelength affects the frequency and vice versa, reinforcing the theoretical concepts discussed throughout the video.
๐Ÿ’กPeriod
The period of a wave is the duration of one complete cycle of the wave. It is the inverse of the frequency, meaning that a higher frequency corresponds to a shorter period, and vice versa. In the video, the period is used to further explain the relationship between frequency and the characteristics of harmonics, such as how a higher harmonic (shorter wavelength) results in a higher frequency and thus a shorter period.
Highlights

Harmonics are integers of the fundamental frequency.

The example of the guitar helps to understand harmonics.

The twelfth fret on a guitar is significant for harmonics.

Fundamental frequency is the whole length of the vibrating string.

Standing waves are created by the interference of waves.

Wavelength is determined by the boundary and frequency.

The fundamental frequency's wavelength is twice the length of the boundary.

Frequency can be calculated using the velocity of the wave divided by the wavelength.

The second harmonic has a wavelength equal to the boundary length.

As harmonics increase, the wavelength decreases and frequency increases.

A 2-meter long string has a fundamental frequency wavelength of 4.0 meters.

The third harmonic's wavelength is two-thirds the length of the boundary.

The frequency of the first harmonic can be calculated using the length and speed of the string.

The period of a wave is the reciprocal of its frequency.

The second harmonic of a 7.5-meter long string has a wavelength of 7.5 meters and a frequency of 0.13 Hertz.

Understanding harmonics and calculating them is essential for analyzing standing waves.

Guitarists use harmonics to create a unique sound when playing.

The first harmonic results in large vibrations and standing waves.

The second harmonic has a node at the end and in the middle.

Transcripts

Browse More Related Video

The Physics of Music: Crash Course Physics #19

Standing Waves on a String, Fundamental Frequency, Harmonics, Overtones, Nodes, Antinodes, Physics

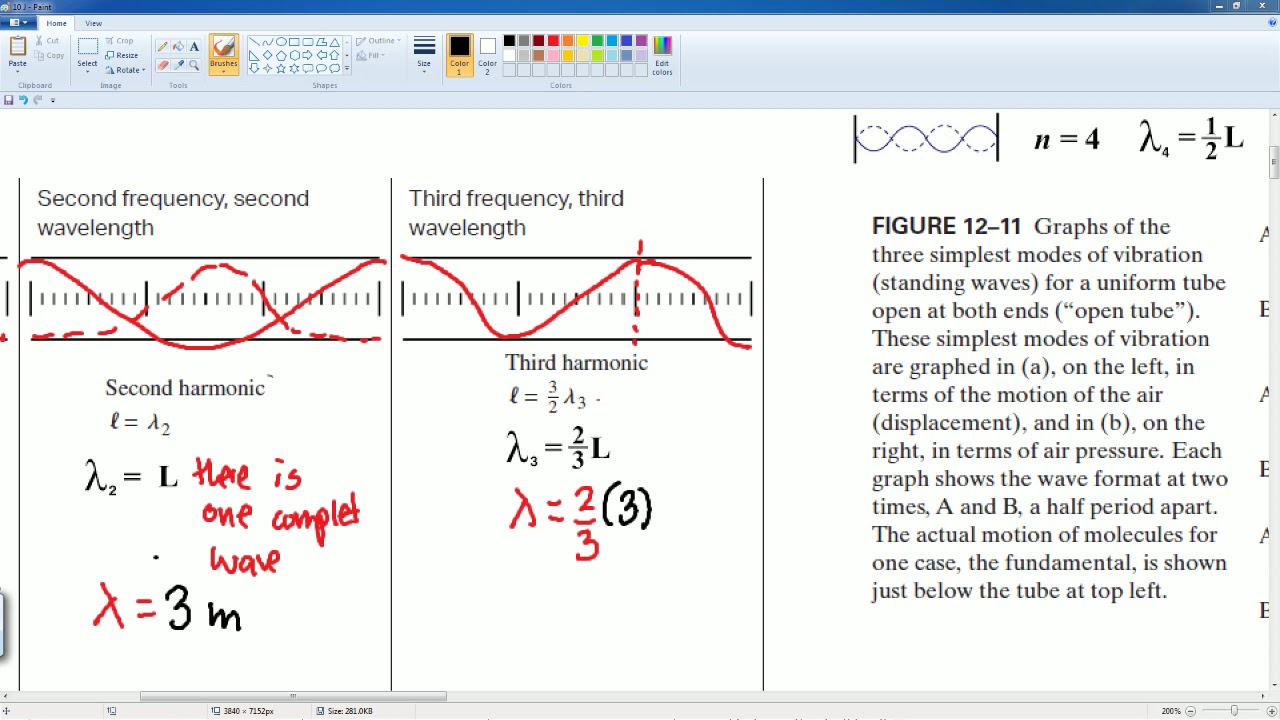
AP Physics Workbook 10.J Standing Waves in Tubes

AP Physics 1 - Standing Waves in Instruments

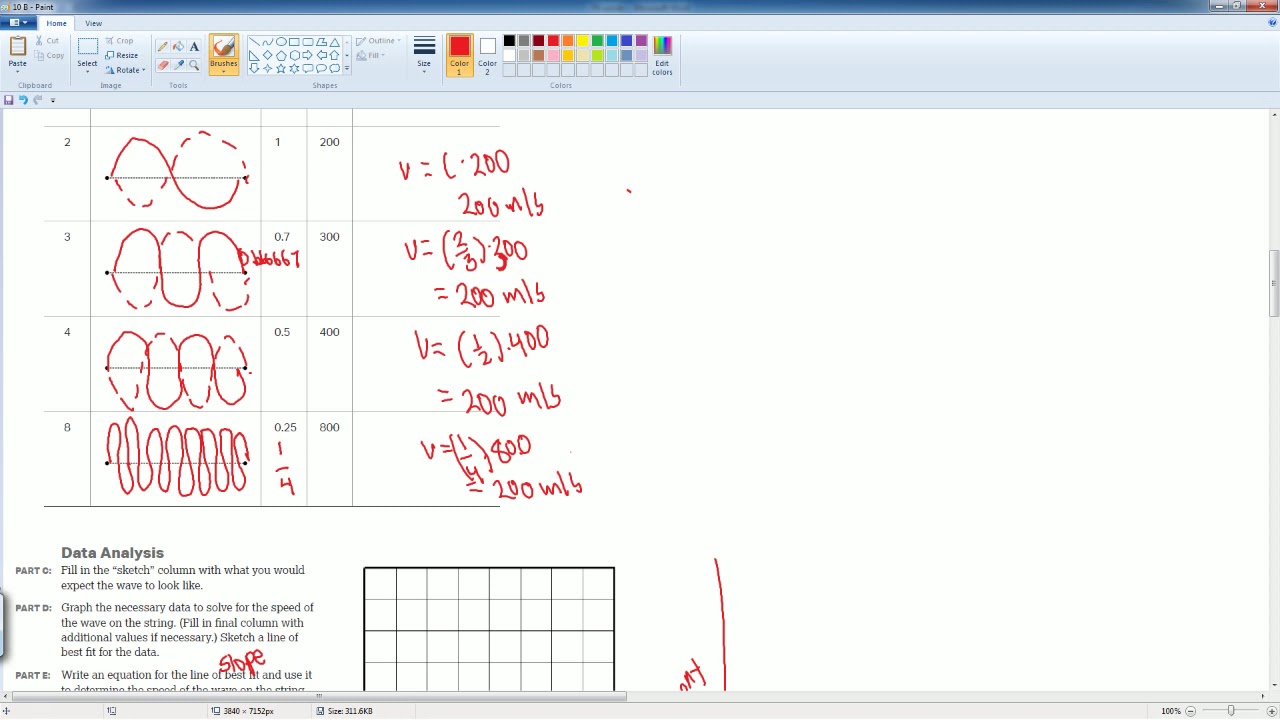
AP Physics Workbook 10.B Relationship Between Wave Speed, Frequency, and Wavelength

Standing waves on strings | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics EssentialsHarmonics ExplainedGuitar DemonstrationStanding WavesFundamental FrequencyWave InterferenceFrequency CalculationAP PhysicsEducational ContentMr. Andersen