Partial Derivatives and the Gradient of a Function

Professor Dave Explains
4 Sept 201910:56
EducationalLearning
32 Likes 10 Comments

TLDRThis lesson reintroduces differentiation notation using d/dx and del operators to represent taking derivatives and gradients. It explains how to take partial derivatives of multivariable functions to find rates of change in specific directions. The gradient vector combines these partial derivatives. An example shows finding a three-dimensional function's gradient by taking its three partial derivatives. The lesson concludes by noting del and gradients have additional applications that will be covered further.

Takeaways
  • 😀 Revisiting differentiation and introducing new notation d/dx as a differential operator that represents taking the derivative
  • 😯 The differential operator d/dx distributes across sums and differences of functions
  • 🧐 Partial derivatives ∂f/∂x allow taking derivatives of multivariable functions with respect to one variable at a time
  • 📝 The gradient combines partial derivatives into a vector showing rates of change
  • 👆 Del (∇) represents a vector of partial derivative operators that can be used to take the gradient
  • 💡 The gradient vector points in the direction of maximum change and has a magnitude equal to the maximum rate of change
  • 📊 Partial derivatives are taken by treating other variables as constants and differentiating normally
  • 🔢 The chain rule still applies when taking partial derivatives
  • 🤔 Variables like x, y and z can be inside of vectors when working with vector fields
  • 🤯 Del has additional uses beyond gradients that will be covered later
Q & A

  • What is the new notation introduced for taking derivatives instead of using f prime?

    -The new notation is d/dx or DF/DX, which represents a differential operator that acts on the function.

  • How can we interpret the rate of change for a function with multiple variables like f(x,y)?

    -We take partial derivatives, like ∂f/∂x and ∂f/∂y, to find the rates of change in specific directions independently.

  • What is the gradient of a multivariable function?

    -The gradient is a vector made up of all the function's partial derivatives, giving the direction of maximum change.

  • What does the del symbol ∇ represent?

    -Del (∇) represents a vector of all the partial derivative operators, so ∇f gives the gradient of f.

  • How do we calculate partial derivatives?

    -Treat the variable you are differentiating with respect to as normal, and treat all other variables as constants.

  • What is an example use of the product rule with the new notation?

    -d/dx(fg) = f dg/dx + g df/dx

  • What is an example use of the chain rule with the new notation?

    -d/dx(f(g(x))) = f'(g(x)) g'(x)

  • Why are we using variables like x and y inside vectors?

    -We are representing partial derivatives and gradients as vectors. This will be discussed more when we cover vector fields.

  • What are some other uses of the del operator?

    -Del has various uses besides gradients, like in curl, divergence, Laplacian, and integration.

  • How can the gradient vector be interpreted geometrically?

    -The gradient points in the direction of maximum increase of the function and has a magnitude equal to the maximum rate of change.

Outlines
00:00
📝 Introducing Partial Derivatives and the Gradient Vector

This paragraph introduces partial derivatives as a way to find the rate of change of a function with multiple variables in specific directions independently. It explains how to take partial derivatives by treating the other variables as constants. It then introduces the gradient vector, which combines all the partial derivatives of a function into a single vector that points in the direction of maximum change.

05:02
📈 Applying Partial Derivatives and the Gradient

This paragraph provides examples of finding partial derivatives and gradients for functions with multiple variables. It shows how to take the partial derivatives by treating other variables as constants and following derivative rules. It explains how to construct the gradient vector from the partial derivatives. An example function is shown and its gradient is derived step-by-step.

Mindmap
Keywords
💡Differentiation
Differentiation is the mathematical process of finding the rate of change of a function. In the video, it's introduced as a foundational concept for understanding how functions change at different points, emphasizing its role in calculating derivatives. Differentiation is crucial for analyzing curves represented by functions, as it helps in determining how quickly or slowly these functions are changing at any given point.
💡Derivative
A derivative represents the rate at which a function changes at any point. The video discusses two notations for derivatives: the prime notation (f') and the differential operator (d/dx), highlighting their utility in understanding function behavior. Derivatives are central to the video's theme as they enable the calculation of slopes and rates of change in various mathematical and real-world contexts.
💡Differential operator
The differential operator, denoted as d/dx, is a symbol used to indicate differentiation with respect to the variable x. The video explains its role in performing differentiation, emphasizing how it acts on functions to produce derivatives. This operator is presented as a versatile tool that distributes across sums and differences, aligning with mathematical rules like the product and quotient rules.
💡Partial derivative
Partial derivatives involve differentiation with respect to one variable while keeping other variables constant. The video introduces this concept to address functions of multiple variables, using the notation ∂/∂x for partial derivatives. This is crucial for understanding the rate of change in multi-dimensional spaces, such as when dealing with surfaces or gradients.
💡Gradient
The gradient is a vector that consists of all partial derivatives of a function, indicating the direction and rate of steepest ascent. The video explains the gradient as a way to generalize the concept of slope to higher dimensions, using the notation grad f and illustrating its computation with examples. The gradient's direction and magnitude provide valuable insights into the function's behavior in multi-dimensional spaces.
💡Vector
A vector is a mathematical entity with both magnitude and direction. In the context of the video, vectors are used to represent gradients and in the notation for partial derivatives. Vectors are essential for understanding and visualizing the direction and magnitude of changes in functions, especially when discussing gradients and vector fields.
💡Rate of change
Rate of change refers to how quickly or slowly a quantity changes over time or another variable. The video uses this concept to describe the essence of differentiation and the computation of derivatives, illustrating how rates of change are foundational to understanding dynamic systems and functions' behaviors.
💡Function
A function is a relation that uniquely associates members of one set with members of another set. The video focuses on functions of one or more variables, discussing their rates of change, partial derivatives, and gradients. Understanding functions and their behavior is crucial for grasping the mathematical concepts presented in the video.
💡Power rule
The power rule is a basic derivative rule used to calculate the derivative of a function of the form x^n. The video utilizes this rule to demonstrate how to find derivatives and partial derivatives, showing its practical application in differentiating polynomial functions. The power rule is presented as an essential tool for simplifying the process of differentiation.
💡Chain rule
The chain rule is a formula to compute the derivative of a composite function. In the video, it is applied in the context of finding the derivative with respect to z in a function involving e^2z, illustrating how to differentiate functions that are compositions of other functions. This rule is pivotal for handling more complex differentiation scenarios.
Highlights

The innovation of using deep learning models to generate highlights from transcripts.

The method of training the deep learning model on a dataset of transcripts and human-generated highlights.

The theoretical contribution of an automated system for highlight generation, reducing the need for manual review.

The practical application of automated highlight generation to improve accessibility of long transcripts.

The potential impact of enabling easier skimming and review of transcripts at scale.

The novelty of generating highlights directly from audio transcripts vs. text summaries.

The use of attention mechanisms in the deep learning model to identify salient points.

The comparison of highlight quality to human-generated highlights as an evaluation method.

The potential to customize highlights for different applications like note-taking or sharing.

The challenge of balancing conciseness and informativeness in highlight generation.

The limitations of current techniques and opportunities for improvement in future work.

The implications for search, discovery and consumption of spoken content at scale.

The ability to provide personalized and dynamic highlights tailored to user needs.

The promise of making transcripts more engaging and accessible to different audiences.

The potential to apply automated highlight generation across domains like education, media, etc.

Transcripts

Browse More Related Video

Gradient 1 | Partial derivatives, gradient, divergence, curl | Multivariable Calculus | Khan Academy

Calculus 3: Directional Derivatives and the Gradient Vector (Video #16) | Math with Professor V

The Gradient of a Function (Calculus 3)

Directional derivative

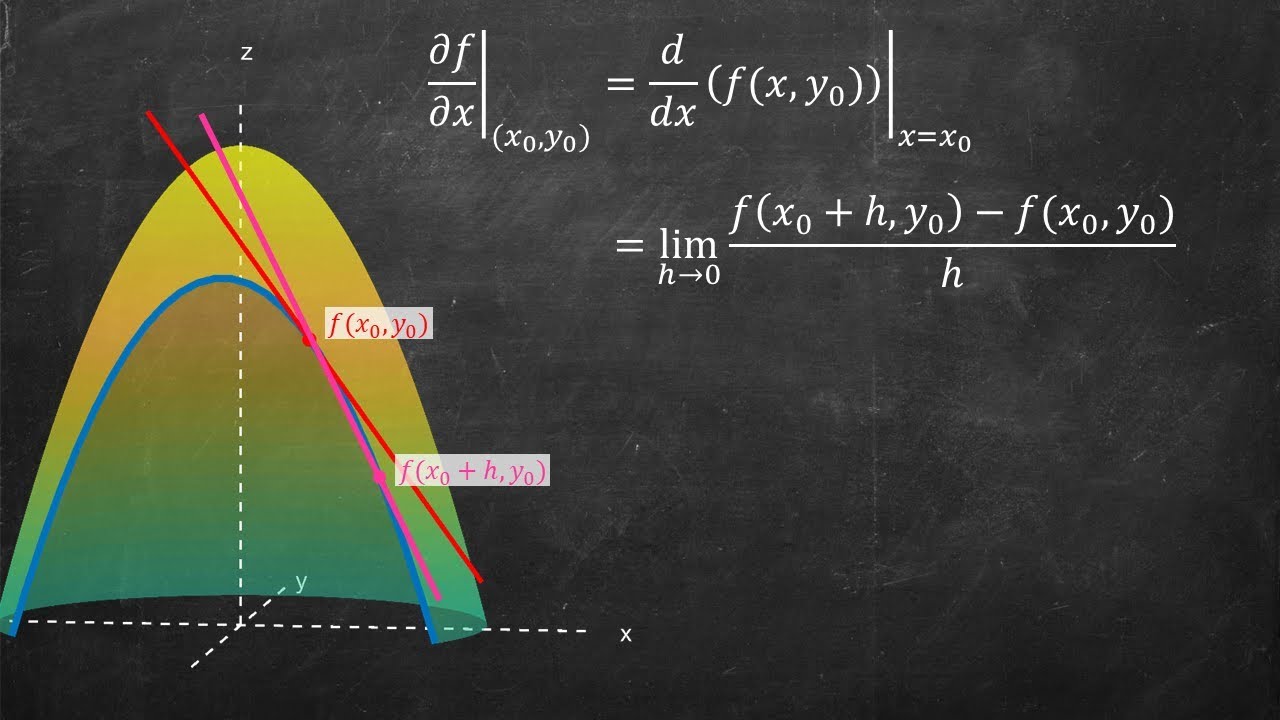
What are derivatives in 3D? Intro to Partial Derivatives

Symmetry of second partial derivatives

Rate This

5.0 / 5 (0 votes)

Thanks for rating: