Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (55 of 92) Solution of the Oscillator

Michel van Biezen
13 Apr 201803:23
EducationalLearning
32 Likes 10 Comments

TLDRThe lecture delves into the solutions of the Schrödinger equation for the simple harmonic oscillator in quantum mechanics. It explains that the total energy is the sum of potential and kinetic energy, with potential energy being proportional to the spring constant and amplitude squared. The wave function solution is quantized and consists of three parts: a normalization constant, an exponential decay term, and a Hermite polynomial that depends on the quantum state. As the quantum number increases, the wave function becomes more complex. The lecture sets the stage for future discussions on normalizing the function and calculating Hermite polynomials for different quantum states.

Takeaways
  • 📝 The lecture focuses on the solutions of the Schrödinger equation for the simple harmonic oscillator in quantum mechanics.
  • 🌟 The potential energy (PE) is given by 1/2 times the spring constant (k) times the amplitude squared (x^2).
  • 🔋 The total energy of the oscillator is always greater than or equal to the potential energy at any point.
  • 📈 The solutions to the Schrödinger equation are quantized, depending on the quantum state of the system.
  • 🔍 The solution to the equation comes in three parts: a normalization constant, an exponential decay function, and a Hermite polynomial.
  • 🌱 The normalization constant is determined by the quantum state and will be explained in future videos.
  • 📉 The exponential decay function (e^(-x^2)) approaches zero as x becomes large, allowing for a smooth function that approaches zero energy.
  • 🎢 Hermite polynomials are polynomials of order N, where N depends on the quantum state.
  • 🚀 For higher quantum states, the wave function solutions become more complex with increasing order of Hermite polynomials.
  • 🔄 The general form of the wave function is a combination of a constant, an exponential decay, and a Hermite polynomial, all dependent on the quantum state.
  • 📚 Future videos will delve into the specifics of Hermite polynomials and their role in the wave function solutions.
Q & A

  • What is the basic premise of the potential energy in the context of the simple harmonic oscillator?

    -The basic premise is that the potential energy is equal to 1/2 times the spring constant times the amplitude squared.

  • How does the total energy of the oscillator relate to the potential energy at any point in time?

    -The total energy of the oscillator is always greater than or equal to the potential energy at any point in time.

  • What is the general form of the Schrödinger equation for the simple harmonic oscillator?

    -The general form of the Schrödinger equation for the simple harmonic oscillator is given by the equation where the total energy is equal to the potential energy, with α^2 defined in terms of the total energy and the potential energy.

  • What are the three parts of the solution to the Schrödinger equation for the simple harmonic oscillator?

    -The three parts of the solution are a constant (found by normalizing the function), an exponential decay function (e^(-x^2)), and a Hermite polynomial.

  • How does the constant in the solution depend on the quantum state?

    -The constant in the solution is quantized and depends on the quantum state, which is determined through the normalization process.

  • What happens to the exponential decay function as x becomes large?

    -As x becomes large, the exponential decay function decays down to the x-axis because e^(-x^2) approaches 0 for large values of x.

  • What is the significance of the Hermite polynomial in the solution?

    -The Hermite polynomial is part of the wave function solution and its order depends on the quantum state, becoming more complicated as the quantum number increases.

  • How does the mass of the oscillator affect the solution?

    -The mass of the oscillator, or more specifically the reduced mass (M), is a factor in the α^2 term, which appears in both portions of the solution.

  • What will be covered in future videos regarding the Hermite polynomials?

    -Future videos will explain what the Hermite polynomials look like and how to calculate them for different quantum states.

  • How does the wave function solution change as the quantum state increases?

    -As the quantum state increases, the wave function solution becomes more complex, with higher-order Hermite polynomials being involved.

  • What is the role of the normalization process in determining the constant in the solution?

    -The normalization process is used to determine the constant in the solution, ensuring that the wave function is properly scaled to represent a probability distribution.

Outlines
00:00
📚 Introduction to Quantum Mechanics and the Simple Harmonic Oscillator

This paragraph introduces the topic of quantum mechanics, focusing on the solutions of the Schrödinger equation for the simple monic oscillator. It explains the basic premise of potential energy being equal to half the spring constant times the amplitude squared. The total energy of the oscillator is discussed, with potential energy being less than or equal to this total energy. The script outlines the equation for the simple harmonic oscillator and introduces the concept of quantization, with the solution depending on the quantum state. The solution is described as having three parts: a normalization constant, an exponential decay function, and a Hermite polynomial, which is detailed to depend on the quantum state and the order of the polynomial.

Mindmap
Keywords
💡Schrodinger Equation
The Schrodinger Equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. In the context of this video, it is used to find the solutions for the simple monic oscillator, which is a model system in quantum mechanics. The solutions to this equation are crucial for understanding the behavior of particles in a potential energy field.
💡Quantum Mechanic Oscillator
A quantum mechanic oscillator is a system that exhibits oscillatory behavior at the quantum level. It is characterized by quantized energy levels, meaning that the energy can only take on certain discrete values. In the video, the focus is on the simple monic oscillator, which is a specific type of quantum oscillator with a potential energy function proportional to the square of its displacement.
💡Potential Energy
Potential energy is the energy an object possesses due to its position in a force field, such as a gravitational or electric field. In the context of the video, the potential energy of the quantum oscillator is given by half the spring constant times the amplitude squared, which represents the energy stored in the system when it is displaced from its equilibrium position.
💡Amplitude
Amplitude, in the context of oscillations, refers to the maximum displacement of a point from its equilibrium position. In the video, the amplitude is related to the potential energy of the simple monic oscillator, and it is squared to determine the potential energy at any point in time.
💡Total Energy
Total energy, in the context of the quantum oscillator, is the sum of the kinetic and potential energies of the system. The video emphasizes that the total energy must be greater than or equal to the potential energy, which is a fundamental principle in understanding the behavior of the quantum oscillator.
💡Reduced Mass
The reduced mass is a concept used in physics to simplify the analysis of systems involving two or more particles. It is the product of the individual masses and the inverse of their mass ratio. In the video, the reduced mass is used in the context of the quantum oscillator to describe the effective mass that influences the system's oscillations.
💡Quantum State
A quantum state is a fundamental concept in quantum mechanics that describes the condition of a quantum system. It is characterized by a wave function, which contains all the information about the system. The video discusses how the solutions to the Schrodinger Equation depend on the quantum state, with different states leading to different wave functions and energy levels.
💡Normalization
Normalization is the process of adjusting a function so that its integral over all space equals one. In quantum mechanics, this ensures that the probability of finding a particle in any state sums up to 100%. The video mentions that the constant in the solution of the Schrodinger Equation for the quantum oscillator will be determined by normalizing the function, which is crucial for obtaining physical quantities from the wave function.
💡Exponential Decay
Exponential decay refers to a process where a quantity decreases rapidly at first and then more slowly as it approaches zero. In the video, the exponential decay is part of the solution to the Schrodinger Equation, where the function e to the minus x squared decays towards the x-axis as x becomes large, indicating that the probability of finding the particle in the quantum state decreases rapidly with distance from the equilibrium position.
💡Hermite Polynomial
Hermite polynomials are a set of orthogonal polynomials that appear in the solutions to the Schrodinger Equation for the quantum harmonic oscillator. They are named after Charles Hermite and are characterized by their order, which corresponds to the quantum state of the system. The video explains that the Hermite polynomial depends on the quantum state and becomes more complex as the quantum number increases.
💡Wave Function
The wave function is a mathematical description of the quantum state of a system in quantum mechanics. It provides information about the probability distribution of a particle's location. In the video, the wave function of the quantum oscillator is composed of three parts: a constant, an exponential decay function, and a Hermite polynomial, all of which depend on the quantum state.
Highlights

The lecture focuses on the solutions of the Schrödinger equation for the simple monic oscillator, also known as the quantum mechanic oscillator.

The potential energy of the oscillator is given by 1/2 times the spring constant times the amplitude squared.

The total energy of the system is related to the amplitude squared and is always greater than or equal to the potential energy at any point.

The Schrödinger equation for the simple monic oscillator is presented in its simple format, showing the relationship between total energy and potential energy.

The solution to the equation comes in three parts: a constant, an exponential decay function, and a Hermite polynomial.

The constant term will be determined by normalizing the function, a process that will be explained in a future video.

The exponential decay function demonstrates that as x becomes large, the solution decays towards the x-axis, approaching zero.

The Hermite polynomial is a key component of the solution and depends on the quantum state of the system.

For the zero quantum state, the Hermite polynomial is simply one, indicating the base case for the polynomial series.

As the quantum state increases, the order of the Hermite polynomial also increases, leading to more complex solutions.

The general form of the wave function is composed of a constant, an exponential decay, and a Hermite polynomial, all of which depend on the quantum state.

The solution structure involves M Omega over H bar and m Omega over H bar, which appears in both portions of the solution, indicating its importance.

The function of the solution is detailed in terms of minus x squared for the exponential decay and the order of X for the Hermite polynomial, showing its variation with quantum state.

The lecture promises to delve into the specifics of the Hermite polynomials in upcoming videos, providing further insight into the wave function solutions.

The wave function's complexity increases with the quantum number, leading to higher order Hermite polynomials and more intricate solutions.

The lecture provides a foundational understanding of the quantum mechanic oscillator, setting the stage for more advanced topics in quantum mechanics.

Transcripts

Browse More Related Video

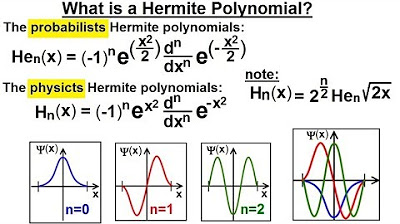
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (56 of 92) What is a Hermite Polynomial?

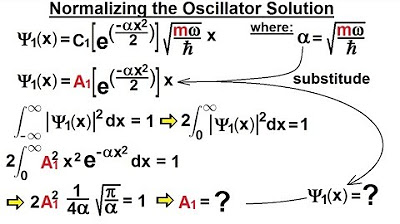
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (60 of 92) Normalizing the Oscillator

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (52 of 92) A Closer Look at the Equation

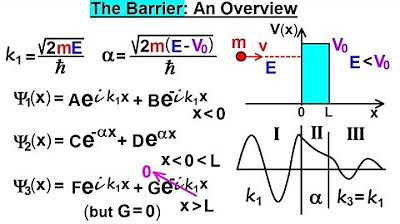
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

Lecture 11: Dispersion of the Gaussian and the Finite Well

24. Quantum Mechanics VI: Time-dependent Schrödinger Equation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsHarmonicOscillatorWaveFunctionsHermitePolynomialsQuantumStatesPhysicsLectureEducationalContentMathematicalAnalysisEnergyPotentialsReducedMass