Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (56 of 92) What is a Hermite Polynomial?

Michel van Biezen
14 Apr 201806:26
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the solutions of the Schrödinger equation for the quantum mechanical oscillator, focusing on the role of Hermitian operators and their graphical representation. It explains the derivation of the physicist Hermite polynomials from the probability Hermite polynomials and how they relate to the physical characteristics of the oscillator. The video outlines the process of normalizing the exponential function to obtain the proper Hermitian polynomials for different energy levels, promising a deeper understanding in subsequent videos.

Takeaways
  • 📚 The lecture focuses on the solutions to the Schrödinger equation for the quantum mechanical oscillator.
  • 🌟 The solutions are referred to as wave functions, which are not probability density functions.
  • 📈 The script discusses the mathematical representation of these wave functions and the challenges in doing so.
  • 🔄 The constant in the function needs to be normalized, relating the spring constant to oscillatory motion.
  • 🤹 The Hermitian operator is identified as the key to representing the solutions graphically.
  • 📊 The Hermitian operator's graphical representation closely resembles the desired function shape.
  • 🌐 The script introduces the concept of Hermite polynomials and their relation to probability Hermite polynomials.
  • 🔢 The method for calculating Hermite polynomials is outlined, involving derivatives and exponential functions.
  • 🔄 A transformation is required to adapt the polynomials to the physical characteristics of the oscillator.
  • 🎯 The solutions for different energy levels (quantum numbers N) are discussed, with specific examples provided.
  • 📝 The next lecture will cover the calculation of these polynomials and the normalization process to obtain a complete set of solutions for the quantum mechanical oscillator.
Q & A

  • What is the main topic of the lecture?

    -The main topic of the lecture is the quantum mechanical oscillator and the solutions to the Schrödinger equation that describe it.

  • What is the significance of the Goofers' quantum mechanic oscillator in the lecture?

    -The Goofers' quantum mechanic oscillator is used as an example to illustrate the concepts of wave functions and their role in quantum mechanics.

  • What does the term 'wave functions' refer to in the context of quantum mechanics?

    -In quantum mechanics, wave functions are mathematical functions that provide information about the probability amplitude of the quantum state of a system.

  • What is the role of the Hermitian operator in the solutions to the Schrödinger equation?

    -The Hermitian operator plays a crucial role in defining the solutions to the Schrödinger equation for the harmonic oscillator, as it allows for the correct representation of the quantum mechanical wave function.

  • How is the function e^(-MΩx^2/ħ) related to the oscillatory motion?

    -The function e^(-MΩx^2/ħ) is a part of the mathematical representation that relates the spring constant to the oscillatory motion in quantum mechanics.

  • What are the two types of equations used to define the Hermitian operators?

    -The two types of equations used to define the Hermitian operators are the Probability Hermite polynomials and the Physicist Hermite polynomials.

  • How can the Physicist Hermite polynomials be derived from the Probability Hermite polynomials?

    -The Physicist Hermite polynomials can be derived from the Probability Hermite polynomials by multiplying them by (π^(1/2) * 2^(n/2)) and considering the function of the square root of 2X instead of just X.

  • How are the Physicist Hermite polynomials calculated?

    -The Physicist Hermite polynomials are calculated by taking (-1)^n times the nth derivative of e^(x^2) with respect to x, and then operating on various functions to obtain the results for different energy levels.

  • What is the significance of normalizing the exponential function in the solutions?

    -Normalizing the exponential function ensures that the probability density function is properly scaled so that the total probability over all space equals one, which is a requirement in quantum mechanics.

  • What is the role of the normalization constant C_sub_n in the quantum state solutions?

    -The normalization constant C_sub_n is used to ensure that the wave function for each quantum state is properly normalized, meaning that the integral of the square of the wave function over all space equals one.

  • How does the lecture plan to further explain the derivation and normalization of the solutions?

    -The lecture plans to show in the next video how to calculate the Hermite polynomials from the given equation and how to normalize the function to obtain the complete set of solutions for the quantum mechanical oscillator.

Outlines
00:00
📚 Introduction to Quantum Mechanics and the Harmonic Oscillator

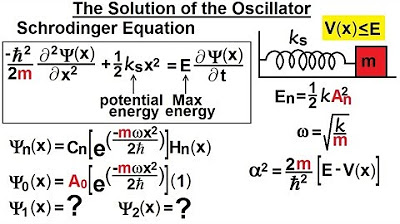
This paragraph introduces the topic of quantum mechanics, specifically focusing on the harmonic oscillator. It discusses the previous video's content, which covered the Goofers, quantum mechanic oscillator, and the solutions to the Schrödinger equation. The speaker clarifies that the solutions are not probability density functions but are referred to as wave functions. The paragraph delves into the mathematical representation of these functions and the challenges in explaining them. It also introduces the concept of operators that help in finding the slope of functions. The speaker then discusses the equation they derived in the previous video to represent the solutions to the Schrödinger equation for the harmonic oscillator, which includes a constant that needs normalization, the spring constant, and the oscillatory motion. The Hermitian operator is highlighted as the key to representing the mathematical equation of the solution. The paragraph ends with a teaser about the upcoming video, where the speaker plans to explain how to calculate the Hermitian polynomials and normalize the function for each quantum state.

05:01
📈 Understanding the Hermitian Polynomials and their Role in Quantum Mechanics

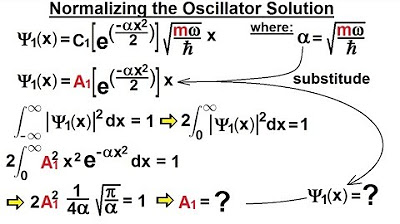
This paragraph continues the discussion on the mathematical representation of quantum mechanics, particularly focusing on the Hermitian polynomials. The speaker explains that these polynomials, along with the exponential decay function, are used to transform the graphical representation of the Hermitian operator. The paragraph details the process of deriving the Hermitian polynomials from the probability Hermite polynomials by multiplying them by a factor and taking the square root of 2 of X. The speaker then describes how these polynomials are calculated by taking the nth derivative of the exponential function with respect to X. The paragraph also explains how to adapt the polynomials to the physical characteristics of the oscillator by replacing X with the square root of M Omega over H bar times X. The speaker concludes by mentioning that the next video will demonstrate the calculation of these polynomials and the normalization process, which will lead to a complete set of solutions for the quantum mechanical oscillator.

Mindmap
Keywords
💡Quantum Mechanics
Quantum Mechanics is a fundamental theory in physics that describes the behavior of matter and energy at the atomic and subatomic scales. In the video, it is the basis for understanding the quantum mechanical oscillator, which is a system that exhibits wave-like behavior.
💡Schrödinger Equation
The Schrödinger Equation is a fundamental partial differential equation in quantum mechanics that describes how the quantum state of a physical system changes with time. In the context of the video, it is used to find the wave functions that describe the quantum mechanical oscillator.
💡Wave Functions
Wave functions are mathematical functions that provide information about the quantum state of a system. They are central to the description of quantum systems and are used to calculate probabilities of various physical quantities. In the video, the讲师 clarifies that the solutions to the Schrödinger Equation are wave functions, not probability densities.
💡Harmonic Oscillator
A harmonic oscillator is a system that oscillates at a constant frequency and is used as a model for many physical systems, including vibrating molecules and electromagnetic waves in a cavity. In the video, the讲师 is discussing the quantum mechanical oscillator, which is a quantum version of the harmonic oscillator.
💡Probability Density
Probability density is a concept in quantum mechanics that describes the likelihood of finding a particle in a particular location. It is related to the square of the absolute value of the wave function. The讲师 clarifies that the solutions to the Schrödinger Equation are not the probability densities themselves, but wave functions.
💡Hermitian Operator
A Hermitian operator, also known as a self-adjoint operator, is an operator in mathematics that is equal to its own complex conjugate when reflected through the complex plane. In quantum mechanics, Hermitian operators correspond to observable quantities, and their eigenvalues represent possible measurements. The讲师 discusses the Hermitian operator as a key component in finding the solutions to the Schrödinger Equation for the harmonic oscillator.
💡Normalization
Normalization in mathematics and physics is the process of adjusting a function so that its integral or sum over all possible values equals one. In quantum mechanics, wave functions are normalized to ensure that the total probability of finding a particle is 100%. The讲师 mentions the need to normalize the function as part of finding the solutions to the Schrödinger Equation.
💡Energy Levels
Energy levels are the quantized states that a quantum system can occupy. In the context of the quantum mechanical oscillator, each level corresponds to a different amount of energy the system can have. The讲师 refers to the energy levels when discussing the quantum states and the Hermitian polynomials.
💡Hermite Polynomials
Hermite polynomials are a set of orthogonal polynomials that are solutions to the Hermite differential equation. They are used in the solutions of the Schrödinger Equation for the quantum harmonic oscillator. The讲师 explains how to derive these polynomials and how they relate to the solutions of the quantum mechanical oscillator.
💡Exponential Decay Function
An exponential decay function is a mathematical function that describes how a quantity decreases exponentially over time. In the context of the video, it is used as part of the mathematical representation of the quantum state of the harmonic oscillator.
💡Quantum Number
A quantum number is a numerical value that describes the state of a quantum system. In the context of the quantum harmonic oscillator, different quantum numbers correspond to different energy levels of the system. The讲师 refers to the quantum number when discussing the solutions for different energy levels.
Highlights

The lecture focuses on the solutions to the Schrödinger equation for the quantum mechanical oscillator.

The solutions are described by wave functions, not probability density functions.

The mathematical representation of these functions is a challenge that the lecture addresses.

A constant is introduced that needs to be normalized in relation to the spring constant and oscillatory motion.

The Hermitian operator is identified as the key to defining the solutions to the Schrödinger equation.

The graphical representation of the Hermitian operator is discussed in relation to the wave functions.

The lecture introduces the concept of physicist Hermite polynomials, derived from probability Hermite polynomials.

The calculation method for Hermite polynomials is explained, involving derivatives and exponential functions.

The polynomials are adapted for the physical characteristics of the oscillator by replacing variables with the square root of M Omega over H bar times X.

The normalization of the exponential function is discussed to bring the function down to the x-axis for large x values.

The hermitian polynomial for each quantum state is used to find the solution for the oscillator.

The process of normalizing the function to get the proper C sub n for each quantum state is mentioned.

The lecture promises to show in the next video how to calculate these polynomials and normalize the function.

A complete set of solutions for the quantum mechanical oscillator will be provided in upcoming videos.

The lecture acknowledges the complexity of the topic but assures that with further videos, the concepts will become clearer.

The importance of understanding the mathematical representation for the quantum mechanical oscillator is emphasized.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (55 of 92) Solution of the Oscillator

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (57 of 92) Calculating Hermite Polynomial?

Lecture 9: Operator Methods for the Harmonic Oscillator

Advanced Quantum Mechanics Lecture 3

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (60 of 92) Normalizing the Oscillator

Ch 9: What are Hermitian operators? | Maths of Quantum Mechanics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsSchrodingerEquationHarmonicOscillatorWaveFunctionsProbabilityDensityHermitianOperatorsPhysicsLectureMathematicalSolutionsQuantumStatesEducationalContent