Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (52 of 92) A Closer Look at the Equation

Michel van Biezen
10 Apr 201803:14
EducationalLearning
32 Likes 10 Comments

TLDRThe lecture clarifies the common confusion in quantum mechanics regarding the different forms of the equation for a quantum mechanical oscillator. It explains that despite appearances, the equations with the operator minus H bar squared over 2m and the second derivative with respect to X of the wave function, plus potential energy terms, are essentially the same. The key is understanding the relationship between the potential energy, the wave function, and the energy of the oscillator, which remains positive or zero. By replacing certain variables with equivalent expressions, the different forms of the equation can be recognized as identical, demystifying the quantum mechanical oscillator's equations.

Takeaways
  • πŸ€” Quantum mechanics equations can appear in different forms, leading to confusion about whether they represent the same or different equations.
  • πŸ“ The equation for a quantum mechanical oscillator is often expressed using the operator -H bar squared over 2m, involving the reduced mass (m).
  • 🌐 The second derivative of the wave function with respect to position (X) and the potential energy as a function of position are key components of the oscillator equation.
  • βš–οΈ The potential energy term (V times X squared) in the equation represents the energy at the maximum amplitude of the oscillator.
  • πŸ”„ The energy E in the equation is always the maximum energy of the oscillator, and V is the potential energy along the path of oscillation.
  • πŸ“ˆ The term alpha squared is defined as 2m over H bar squared times E minus V sub X, and it is always positive or zero, indicating the stability of the system.
  • πŸ”„ By replacing alpha squared and rearranging the equation, we can express it in a form that looks different but is fundamentally the same as the original.
  • πŸŒ€ The potential energy term can be rewritten using the spring constant (K) or as M Omega squared, showing the relationship between different notations.
  • πŸ’‘ Understanding the equivalence of different forms of the quantum mechanical oscillator equation helps to clarify the underlying principles and avoid confusion.
  • πŸ“š It's important to recognize that different notations can represent the same physical concepts, allowing for a deeper comprehension of quantum mechanics.
  • πŸ” When encountering different forms of the same equation, careful analysis of the terms and their relationships can reveal their true equivalence.
Q & A

  • What is the main topic of the lecture?

    -The main topic of the lecture is the understanding of different forms of the equation for a quantum mechanical oscillator in quantum mechanics.

  • Why does confusion arise in quantum mechanics when seeing equations in different formats?

    -Confusion arises because it might not be immediately clear whether the different formats represent the same or a different equation, especially when dealing with the quantum mechanical oscillator.

  • What is the significance of the reduced mass (m) in the equation for a quantum mechanical oscillator?

    -The reduced mass (m) is a crucial parameter in the equation for a quantum mechanical oscillator, as it represents the effective mass of the oscillator system and is used in the calculation of the oscillator's energy levels.

  • How is the potential energy of an oscillator expressed in the equation?

    -The potential energy of an oscillator is expressed as V times X squared (VX^2), where V is the potential energy as a function of position and X is the position variable.

  • What does the term 'alpha squared' represent in the context of the quantum mechanical oscillator?

    -Alpha squared (Ξ±^2) is a constant defined as 2m over H bar squared (2m/H^2), which is used in the reformulation of the oscillator's energy equation.

  • What is the relationship between the potential energy V and the energy E of the oscillator?

    -The potential energy V is always equal to 0 or a number larger than 0 (never smaller than 0), and it represents the potential energy anywhere along the path of oscillation. The energy E is the maximum energy of the oscillator, and they are related through the equation.

  • How can the equation be rewritten using the spring constant K and angular frequency Omega?

    -The equation can be rewritten by replacing K with Omega times m (K = mΞ©^2), which allows expressing the potential energy term as one-half KX squared (1/2 KX^2) in terms of the spring constant and angular frequency.

  • What is the significance of recognizing that different forms of the equation represent the same thing?

    -Recognizing that different forms represent the same equation helps to avoid confusion and facilitates a deeper understanding of the quantum mechanical oscillator's behavior and energy dynamics.

  • How does the process of moving terms around in the equation help in understanding the quantum mechanical oscillator?

    -Moving terms around in the equation allows for the rearrangement of the formula in a way that can simplify the understanding of the relationships between different quantities, such as energy levels and potential energy, in the context of the quantum mechanical oscillator.

  • What is the role of the second derivative of the wave function in the equation?

    -The second derivative of the wave function with respect to X is a key component in the equation, representing the rate of change of the wave function's slope, which is crucial in determining the oscillator's energy states.

  • What does the equality of the wave function multiplied by energy and potential energy terms indicate?

    -The equality indicates that the total energy of the system (the sum of kinetic and potential energies) is constant and equal to the eigenvalue E, which represents the maximum energy of the oscillator.

Outlines
00:00
πŸ“š Understanding Quantum Mechanics Equations

This paragraph discusses the common confusion that arises when encountering quantum mechanics equations in different formats. It uses the example of a quantum mechanical oscillator to illustrate how the energy equations can be expressed in various ways. The paragraph explains the relationship between the potential energy as a function of position and the maximum energy obtained at maximum amplitude. It clarifies that despite appearances, different forms of the equation actually represent the same concept, thus demystifying the seemingly complex world of quantum mechanics equations.

Mindmap
Keywords
πŸ’‘Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. In the video, the speaker discusses the complexities and confusion that can arise when dealing with quantum mechanics, particularly when equations appear in different forms.
πŸ’‘Equations
Equations in the context of the video refer to the mathematical expressions used to describe the behavior of quantum mechanical systems. The speaker emphasizes the importance of recognizing that different forms of an equation can represent the same physical situation, which is crucial for understanding quantum mechanics.
πŸ’‘Quantum Mechanical Oscillator
A quantum mechanical oscillator is a system that exhibits oscillatory behavior at the quantum level, such as a diatomic molecule or a particle attached to a spring. The video explains how the equation for such an oscillator can be expressed in various forms, which might look different but are fundamentally the same.
πŸ’‘Operator
In quantum mechanics, an operator is a mathematical function that acts on a wave function to produce another wave function. The script mentions the operator in the context of the equation for a quantum mechanical oscillator, where it is used to describe the energy states of the system.
πŸ’‘Wave Function
The wave function is a mathematical description of the quantum state of a system in quantum mechanics. It contains all the information about the system's physical properties and is used to calculate probabilities of various outcomes. In the video, the wave function is central to understanding the quantum mechanical oscillator's behavior.
πŸ’‘Reduced Mass
The reduced mass is a concept used in the description of systems involving two or more particles, such as a diatomic oscillator. It is a weighted average of the masses of the particles, which simplifies the equations of motion in such systems. The video script mentions the reduced mass in the context of the quantum mechanical oscillator's equation.
πŸ’‘Potential Energy
Potential energy is the energy that a system possesses due to its position or configuration. In the context of the quantum mechanical oscillator, the potential energy is a function of position and is related to the system's energy states. The video script explains how potential energy is represented in the oscillator's equation.
πŸ’‘Energy
In physics, energy is the capacity to do work or the ability to cause change. In quantum mechanics, energy is a key property of a system's state, often quantified by the energy levels of the wave function. The video script discusses the maximum energy of a quantum mechanical oscillator and how it relates to the system's potential and kinetic energies.
πŸ’‘Amplitude
Amplitude in the context of oscillations refers to the maximum displacement of a point from its equilibrium position. In the video, the maximum amplitude is used to describe the highest point in the oscillation of the quantum mechanical oscillator.
πŸ’‘Spring Constant
The spring constant, often denoted by 'k', is a measure of a spring's stiffness. It determines the amount of force needed to compress or extend the spring by a given distance. In the quantum mechanical oscillator model, the spring constant is a key parameter in the equation describing the system's behavior.
πŸ’‘Omega
In the context of the video, 'Omega' is a symbol used to represent a specific frequency-related quantity in the equations describing a quantum mechanical oscillator. It is related to the angular frequency of the oscillator, which is a key factor in determining the system's energy levels and dynamics.
Highlights

Confusion in quantum mechanics often arises from different formats of the same equation.

The quantum mechanical oscillator's equation can be expressed in various forms.

The equation for an oscillator is written with the operator minus H bar squared over 2m.

The potential energy in the oscillator equation is a function of position multiplied by the wave function.

The maximum energy of an oscillator is obtained at maximum amplitudes.

The potential energy as a function of position can range between 0 and the maximum amplitude.

The quantity alpha squared is defined as 2m over H bar squared times e minus V sub X.

Since E is the maximum energy, V will be the potential energy along the path of oscillation, always non-negative.

The equation can be rewritten with the second derivative of the wave function squared equal to negative alpha squared times the wave function.

By multiplying both sides by H bar squared over 2m, the equation can be rearranged.

The potential energy of the oscillator as a function of X is represented by one-half KX squared.

K can be replaced by Omega M times Omega squared to express the equation in a different format.

The two different forms of the quantum mechanical oscillator equation are fundamentally the same.

Understanding the equivalence of different forms of the same equation can alleviate confusion in quantum mechanics.

The lecture aims to clarify the differences and similarities between various expressions of the quantum mechanical oscillator equation.

The wave function and its derivatives play a crucial role in the quantum mechanical oscillator equation.

The reduced mass m is a key parameter in the oscillator equation.

The spring constant K is related to the oscillator's potential energy function.

The lecture provides a detailed explanation of the quantum mechanical oscillator's equation, enhancing understanding of quantum mechanics.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (53 of 92) The wave Equation

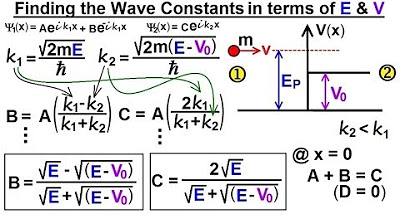
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (66 of 92) B=? C=? in terms of E & V0

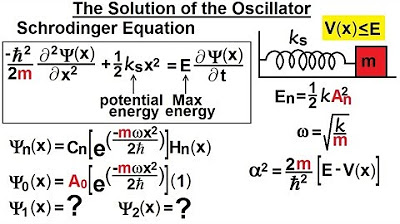
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (55 of 92) Solution of the Oscillator

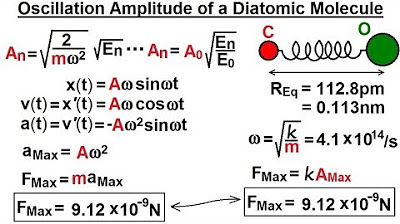
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (51 of 92) Oscillator Amplitude - Diatomic

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (38 of 92) Simple Harmonic Oscillator

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsHarmonicOscillatorEquationAnalysisEnergyStatesPhysicsLectureMathematicalDerivationsEducationalContentOnlineLearningScienceEnlightenmentWaveFunctionsPotentialEnergy