Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (60 of 92) Normalizing the Oscillator

Michel van Biezen
18 Apr 201803:00
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the process of normalizing the wave function for the quantum harmonic oscillator, derived from the Schrödinger equation. It explains the calculation of the constant c1 for the quantum state n=1 and the subsequent creation of a new constant a1 through normalization. The script details the integration process, taking advantage of the function's symmetry to simplify the integral from negative infinity to infinity to one from 0 to infinity. The final result is the normalized function, which matches the previously discussed general solution for the quantum harmonic oscillator.

Takeaways
  • 📚 The lecture focuses on normalizing a function related to the Schrödinger equation for a quantum mechanical oscillator.
  • 🔍 The specific quantum state being discussed is n=1, with a constant c1 to be determined.
  • 🌐 The general solution for the quantum state n=1 is given by a formula involving exponential, constant factors, and the variable x.
  • 🔧 The process of normalization involves creating a new constant a1 from c1 and ensuring the integral of the function squared equals 1.
  • 📈 Due to symmetry, the integration can be simplified by evaluating from 0 to infinity and multiplying by 2.
  • 🧮 The integral equation is used to simplify the process, with a key integral involving the square root of pi over alpha.
  • 🎛️ The constant alpha is defined in terms of mass (M), angular frequency (Omega), and reduced Planck's constant (H-bar).
  • 🔄 By replacing alpha with its definition and simplifying, the final normalized constant a1 is obtained.
  • 🌟 The normalized a1 matches the general solution for the quantum harmonic oscillator, confirming the correctness of the process.
  • 📊 The list of integrals from a previous video is crucial for solving the normalization problem efficiently.
  • 🎓 The lecture demonstrates the methodical approach to normalizing functions in quantum mechanics, which is essential for accurate physical modeling.
Q & A

  • What is the Schrödinger equation mentioned in the script?

    -The Schrödinger equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time.

  • What is the significance of normalizing a function in quantum mechanics?

    -Normalization of a function in quantum mechanics is important to ensure that the probability of finding a particle in any region of space adds up to 1, which is a requirement of the probability interpretation of the wave function.

  • What does the constant c1 represent in the context of the script?

    -In the context of the script, the constant c1 is a coefficient in the general solution for the quantum state n equals 1 of the harmonic oscillator.

  • How is the new constant a1 derived in the script?

    -The new constant a1 is derived by adding the constant c1 to create a1, and then normalizing a1 by integrating the function squared from 0 to infinity and setting the integral equal to 1.

  • Why is the integration done from 0 to infinity instead of from minus infinity to infinity?

    -Due to the symmetry of the function, integrating from 0 to infinity and then multiplying by 2 is equivalent to integrating from minus infinity to infinity, which simplifies the calculation for normalization.

  • What is the role of the integral equation in the normalization process?

    -The integral equation is used to simplify the calculation of the integral of the function squared. It helps in determining the value of the constant after normalization by using known integrals from previous materials.

  • What is the significance of the square root of 2 alpha and the 4th root of alpha in the final equation?

    -The square root of 2 alpha and the 4th root of alpha are significant as they represent the coefficients that ensure the function is properly normalized. These values are derived from the constants and parameters of the quantum harmonic oscillator.

  • How does the script relate the normalized function to the general solution for the quantum state n equals 1?

    -The script shows that after normalizing the function and finding the constant a1, the resulting equation matches the general solution for the quantum state n equals 1, confirming that the normalization process was done correctly.

  • What is the physical interpretation of the normalized function?

    -The normalized function represents the wave function of the quantum harmonic oscillator in the quantum state n equals 1, where the probability of finding the particle in a particular region of space is given by the square of the wave function's magnitude.

  • How does the script use the relationship between alpha, M, Omega, and H-bar?

    -The script uses the relationship between alpha, M, Omega, and H-bar to express the constant a1 in terms of the physical parameters of the quantum harmonic oscillator, which are the mass (M), the angular frequency (Omega), and the reduced Planck constant (H-bar).

  • What is the final result of the normalization process?

    -The final result of the normalization process is the determination of the constant a1, which when multiplied by the general solution for the quantum state n equals 1, gives a properly normalized wave function for the quantum harmonic oscillator.

Outlines
00:00
📚 Normalization of Quantum Harmonic Oscillator Function

The paragraph discusses the process of normalizing a function in quantum mechanics, specifically for the quantum harmonic oscillator. It begins with the introduction of the Schrödinger equation for quantum state n=1 and the general solution involving a constant c1. The speaker then explains how to add this constant to create a new constant a1 and the subsequent steps to normalize a1 by squaring the function and integrating it from 0 to infinity. Due to symmetry, the integration can be done from 0 to infinity and multiplied by 2. The normalization condition is set to equal 1. The integral equation is used, and the constant is isolated to find the value of a1. The speaker then relates this back to the general solution and shows that the derived equation matches the initial one, thus confirming the normalization process.

Mindmap
Keywords
💡Quantum Mechanics
Quantum Mechanics is a fundamental theory in physics that describes the behavior of matter and energy at the atomic and subatomic scales. It provides a framework for understanding the interactions and properties of particles in the quantum realm. In the video, the speaker is discussing the Schrödinger equation, which is a core equation in quantum mechanics that describes how quantum states evolve over time.
💡Schrödinger Equation
The Schrödinger Equation is a fundamental partial differential equation in quantum mechanics that describes the state of a quantum system over time. It is named after Erwin Schrödinger, one of the founders of quantum mechanics. The equation is used to determine the wave function of a system, which contains all the information about the system's quantum state.
💡Quantum State
In quantum mechanics, a quantum state is the fundamental concept that describes the condition of a quantum system. It is represented by a mathematical function called a wave function, which contains all the possible outcomes of measurements that can be performed on the system. The quantum state evolves according to the Schrödinger equation.
💡Harmonic Oscillator
A harmonic oscillator is a system that oscillates at a constant frequency when displaced from its equilibrium position. In the context of quantum mechanics, the quantum harmonic oscillator is a theoretical model that describes particles in a periodic potential. It is used to understand phenomena such as the vibrational states of molecules and the quantization of energy levels.
💡Normalization
Normalization in mathematics, particularly in the context of functions, refers to the process of adjusting a function so that its integral over a certain domain equals 1. This is important in quantum mechanics because it ensures that the probability of finding a particle in a particular state sums up to 1, which is a requirement of the probability interpretation of quantum mechanics.
💡Constant C1
In the context of the script, constant C1 refers to a coefficient that is part of the solution to the Schrödinger equation for a specific quantum state. This constant is determined by the conditions of the problem and is crucial for ensuring that the wave function satisfies the physical requirements of the system, such as normalization.
💡Wave Function
A wave function is a mathematical description of the quantum state of a system in quantum mechanics. It provides information about the probability distribution of a particle's location, momentum, and other physical properties. The wave function is central to the formulation of quantum mechanics and is used to calculate the probabilities of various outcomes when measurements are made.
💡Integral
In mathematics, an integral represents the accumulation of a quantity over a given range or region. In the context of physics and specifically quantum mechanics, integrals are used to calculate probabilities and other physical quantities. The process of integration is essential for normalizing wave functions and solving differential equations.
💡Symmetry
Symmetry in mathematics and physics often refers to the property of an object or function that allows it to be mapped onto itself in a certain way. In the context of the script, symmetry is used to simplify the process of normalization by allowing the integral to be calculated over a limited range (from 0 to infinity) instead of the entire range (from negative infinity to infinity).
💡Alpha
In the context of the script, Alpha (α) is a constant that appears in the mathematical expressions related to the quantum harmonic oscillator. It is defined in terms of the mass (M), angular frequency (Ω), and the reduced Planck constant (ħ). Alpha plays a crucial role in determining the properties of the quantum state and the normalization constant.
💡Probability Interpretation
The probability interpretation is a fundamental concept in quantum mechanics that states that the absolute square of the wave function represents the probability density of finding a particle in a particular state or location. This interpretation is essential for understanding the statistical nature of quantum mechanics and the predictions it makes about the outcomes of measurements.
Highlights

The lecture introduces the process of normalizing a function in the context of quantum mechanics.

The Schrödinger equation is discussed, which is fundamental in describing quantum mechanical systems.

The specific focus is on the quantum mechanical oscillator and its corresponding quantum state n equals 1.

A constant c1 is being determined as part of the normalization process.

The general solution for the quantum state n equals 1 is provided, involving an exponential function and a square root term.

Normalization involves creating a new constant a1 from c1 and ensuring the integral of the function squared equals 1.

Due to symmetry, the integration can be simplified by considering the interval from 0 to infinity and multiplying by 2.

The integral equation is manipulated to isolate the constant, showcasing a key step in the normalization process.

A list of integrals from a previous video is referenced, highlighting the importance of prior knowledge in solving the problem.

The final form of the normalized constant a1 is derived, involving the square root of 2 alpha and other parameters.

The derived constant a1 is related back to the original equation, confirming the correctness of the normalization process.

The process demonstrated is crucial for describing the quantum harmonic oscillator accurately.

The lecture provides a clear and methodical approach to normalizing functions in quantum mechanics.

The mathematical steps are detailed, offering a comprehensive understanding of the normalization process.

The use of integral tables and previous knowledge is emphasized, showing the interconnected nature of quantum mechanics concepts.

The final equation obtained matches the general solution, validating the normalization method used.

Transcripts

Browse More Related Video

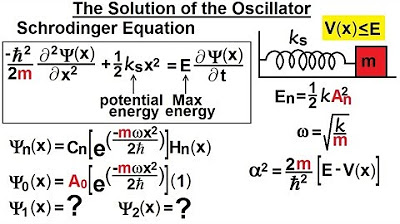
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (55 of 92) Solution of the Oscillator

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (57 of 92) Calculating Hermite Polynomial?

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (53 of 92) The wave Equation

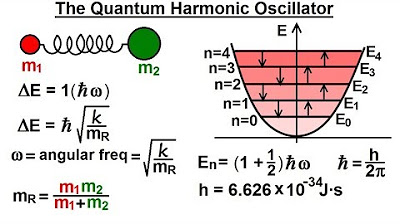
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (39 of 92) What is the Quantum Oscillator?

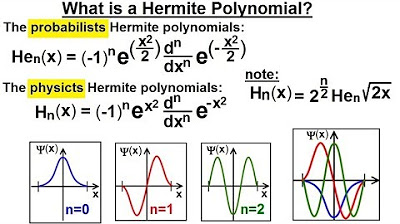
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (56 of 92) What is a Hermite Polynomial?

Advanced Quantum Mechanics Lecture 3

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsSchrodingerEquationHarmonicOscillatorMathematicalPhysicsNormalizationProcessEducationalContentTheoreticalPhysicsQuantumStatesConstantIntegration