Calculus AB/BC – 6.7 The Fundamental Theorem of Calculus and Definite Integrals
TLDRIn this educational video, Mr. Bean humorously delves into the Fundamental Theorem of Calculus, emphasizing the connection between anti-derivatives and definite integrals. He explains how anti-derivatives can represent the area under a curve, and demonstrates the process of finding anti-derivatives using the power rule. Mr. Bean also illustrates the concept with examples and highlights the importance of understanding this theorem for grasping integral calculus. The video concludes with a practical application, showing how to calculate the accumulation of change using the derivative of a function.
Takeaways
- 📚 The Fundamental Theorem of Calculus links anti-derivatives with definite integrals, representing the area under a curve.
- 🔄 Anti-derivatives are functions whose derivative is the original function, essentially reversing the process of differentiation.
- 📈 The power rule for anti-derivatives involves adding one to the exponent and then dividing by the new exponent.
- 🌠 The anti-derivative of a function can be represented with a plus constant (C), acknowledging an infinite number of potential anti-derivatives.
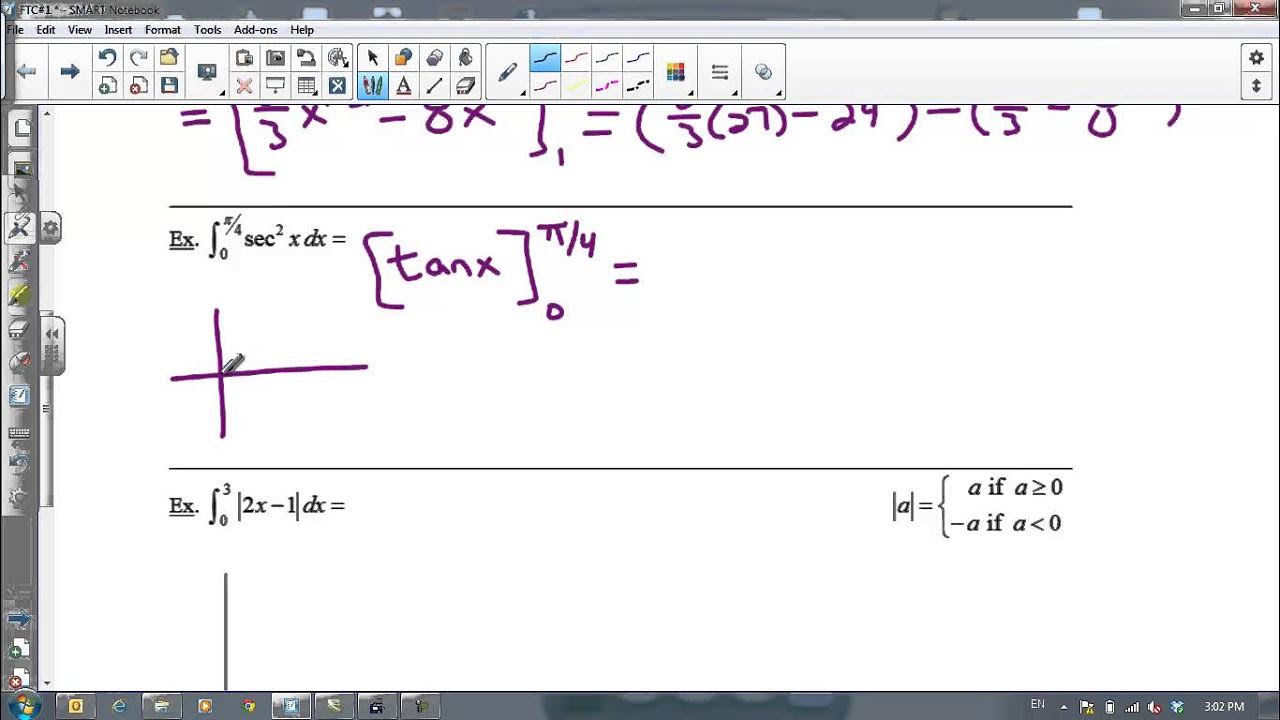
- 📊 The area under a curve from point a to b is calculated by evaluating the antiderivative at the upper bound and subtracting the evaluation at the lower bound.
- 🔢 For integrals involving constants, the anti-derivative is the constant itself, as the derivative of a constant is zero.
- 🌐 The anti-derivative of sine(x) is cosine(x) + C, and the anti-derivative of cosine(x) is -sine(x) + C.
- 📌 The process of finding anti-derivatives can be simplified by multiplying by reciprocals instead of dividing by fractions.
- 📈 The Fundamental Theorem of Calculus Part 1 allows for the quick calculation of a definite integral using the antiderivative of the function.
- 🔄 The process of integration can be used to find the accumulated change in a function over an interval, given the function's derivative and a point on the function.
- 🎓 Understanding the concept of anti-derivatives and the Fundamental Theorem of Calculus is crucial for solving more complex integral problems.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is the Fundamental Theorem of Calculus and its connection with definite integrals.
What is an anti-derivative?
-An anti-derivative of a function is a function whose derivative is the original function.
How is the area under a curve represented in the context of integrals?
-The area under a curve from point a to point b is represented by taking the antiderivative of the function and evaluating it between the bounds a and b.
What is the power rule for anti-derivatives?
-The power rule for anti-derivatives involves adding 1 to the exponent of the variable and then dividing by the new exponent.
Why is the constant 'c' included when finding an antiderivative?
-The constant 'c' is included because it represents the family of functions that could be the antiderivative, accounting for different possible constant values.
What is the significance of the Fundamental Theorem of Calculus in this lesson?
-The Fundamental Theorem of Calculus is significant as it provides a method to calculate the definite integral of a function by using its antiderivative.
How does the antiderivative of sine and cosine functions relate to their derivatives?
-The antiderivative of sine is cosine, and the antiderivative of cosine is negative sine, reflecting the relationship between their derivatives.
What is the process for finding the antiderivative of a sum of functions?
-To find the antiderivative of a sum of functions, you find the antiderivative of each function separately and then add them together.
How does the Fundamental Theorem of Calculus help in finding the net change between two points?
-The Fundamental Theorem of Calculus allows you to find the net change between two points by evaluating the antiderivative (area under the curve) of the function's derivative over the interval between those points.
What is the final result of the example where the antiderivative of x^(-2) is evaluated from 1 to 4?
-The final result of the example is 3.9167, which is the value of the antiderivative evaluated from 1 to 4.
How does the antiderivative help in finding the function value at a specific point when given a function's derivative and a point?
-The antiderivative helps by providing the accumulated change of the function from one point to another, which can be used to find the function's value at the new point.
Outlines
📚 Introduction to Anti-Derivatives and the Fundamental Theorem of Calculus
This paragraph introduces the concept of anti-derivatives and their relationship with definite integrals. Mr. Bean explains that understanding anti-derivatives is crucial for grasping integrals, just as the power rule is essential for derivatives. He uses the power rule as an analogy, illustrating how an anti-derivative undoes the operation of differentiation. The paragraph also touches on the historical aspect of calculus, mentioning that even Isaac Newton and Gottfried Leibniz did not initially recognize the connection between anti-derivatives and areas under curves. The explanation includes a step-by-step guide on how to find anti-derivatives, emphasizing the importance of adding one to the exponent and dividing by the new exponent.
📈 Calculating Anti-Derivatives and the Fundamental Theorem of Calculus
This section delves into the specifics of calculating anti-derivatives, using the power rule as an example. Mr. Bean clarifies the process of finding anti-derivatives by adding one to the exponent and dividing by the new exponent. He corrects a common mistake made by students when dealing with negative exponents. The paragraph then transitions to the fundamental theorem of calculus, explaining how the anti-derivative of a function can be used to find the area under a curve between two points. Mr. Bean demonstrates this with a practical example, calculating the area under a straight line from x = -2 to x = 5.
🌟 Anti-Derivatives of Sine and Cosine Functions
This paragraph focuses on the anti-derivatives of sine and cosine functions. Mr. Bean explains that the antiderivative of sine is cosine plus a constant, and vice versa, but with a negative sign for cosine. He emphasizes the importance of memorizing derivatives to easily find anti-derivatives and suggests verifying the results by taking the derivative of the anti-derivative. The explanation is supplemented with a practical example, calculating the area under a curve with a function involving both sine and cosine terms.
🔢 Applying the Fundamental Theorem of Calculus to Find Function Values
The final paragraph discusses the application of the fundamental theorem of calculus to find the value of a function at a specific point, given the derivative and a point on the function. Mr. Bean illustrates this by finding the value of a function at x = 3, knowing the function's derivative and a point on the function at x = 1. He explains that the integral of the derivative from 1 to 3 will give the net change in the function's value, which can then be used to find the function's value at the new point. The explanation concludes with a practical calculation that confirms the process.
Mindmap
Keywords
💡Fundamental Theorem of Calculus
💡Antiderivatives
💡Definite Integrals
💡Power Rule
💡Constant of Integration
💡Area Under the Curve
💡Derivatives
💡Integration
💡Rate of Change
💡Net Change
Highlights
Introduction to the fundamental theorem of calculus and its connection with definite integrals.
Explanation of anti-derivatives and their relationship with derivatives.
Illustration of how anti-derivatives represent the area under the curve in integrals.
Detailed explanation of the power rule for anti-derivatives, including the steps for finding the anti-derivative of a function.
Discussion on the necessity of understanding the fundamental theorem of calculus for integrals, similar to the power rule for derivatives.
Example of finding the anti-derivative of a polynomial function and the inclusion of the constant 'c'.
Clarification on the anti-derivative process for constants and the resulting function.
Rewriting complex functions into simpler forms to identify exponents for anti-derivatives.
Demonstration of finding the anti-derivative of functions involving both positive and negative exponents.
Explanation of the anti-derivatives of sine and cosine functions and their integrals.
Application of the fundamental theorem of calculus to calculate the area under a linear function's curve.
Use of the fundamental theorem of calculus to evaluate a function at a specific point given its derivative and a point on the function.
Emphasis on the importance of memorizing derivatives for easier application in finding anti-derivatives.
Final summary and encouragement for students to practice the techniques learned in the lesson.
Transcripts
Browse More Related Video

Calculus AB/BC – 6.4 The Fundamental Theorem of Calculus and Accumulation Functions
Fundamental Theorem of Calculus

Mastering Calculus: An Introduction to Integrals

Fundamental Theorem of Calculus 1 | Geometric Idea + Chain Rule Example

Fundamental theorem of calculus (Part 1) | AP Calculus AB | Khan Academy
Average Value of a Function Over an Interval - Calculus
5.0 / 5 (0 votes)
Thanks for rating: