Mastering Calculus: An Introduction to Integrals
TLDRThis transcript delves into the concepts of derivatives and integrals, fundamental to calculus. It explains how derivatives represent the slope of a curve and introduces various techniques for calculating them. The focus then shifts to integrals, emphasizing their role as anti-derivatives and their practical application in determining the area under a curve. The video outlines the basic rules for integrating polynomials and trigonometric functions, highlighting the importance of the constant of integration. The transcript also introduces the fundamental theorem of calculus, which connects integrals to the calculation of areas under curves, providing a powerful tool for solving real-world problems in fields like engineering and physics.
Takeaways
- 📚 Derivatives and integrals are fundamental concepts in calculus, with derivatives representing the slope of a curve and integrals representing the area under a curve.
- 🔄 The process of taking a derivative involves using techniques like the chain rule and multiplication rule, while integrating often requires finding the antiderivative or original function.
- 🔢 Integration can be more challenging than differentiation, especially for complex functions, and sometimes requires the use of a computer to solve.
- 🌐 Integrals have real-world applications in fields like engineering and physics, where they are used to solve problems that cannot be easily tackled without them.
- 📈 The concept of an indefinite integral is introduced as a general problem without definite bounds, whereas a definite integral has specific numerical limits.
- 🎓 The fundamental theorem of calculus states that the definite integral of a function from A to B is equal to the antiderivative evaluated at B minus the antiderivative evaluated at A.
- 📊 The area under a curve can be calculated using integrals by summing up the areas of infinitesimally small rectangles under the curve.
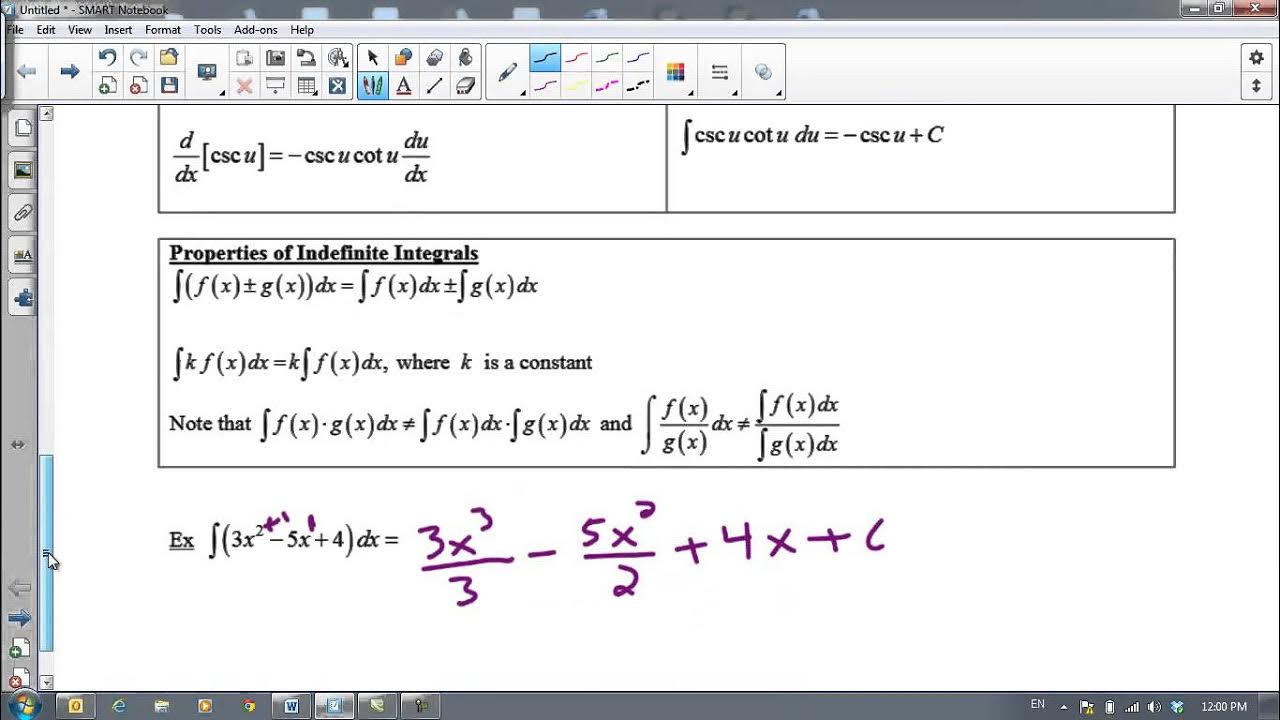
- 📌 The properties of integrals include the ability to factor out constants, the sum of integrals being the integral of the sum, and the addition of a constant to the integrated function.
- 📐 The process of integration involves adding 1 to the exponent of the function when applying the basic formula for integrating polynomials.
- 🌟 Trigonometric functions have specific integrals that can be derived from their derivatives, such as the integral of cosine being sine plus a constant.
- 📝 Memorizing the properties and basic formulas for integrals is crucial for solving calculus problems and understanding the underlying concepts.
Q & A
What is the main concept of taking derivatives discussed in the transcript?
-The main concept discussed is that taking derivatives involves using specific techniques such as the chain rule and multiplication rule to repeatedly take derivatives until there's nothing left to differentiate. It's a mechanical process that involves moving from the outermost function to the innermost and multiplying everything together along the way.
How does the process of integration differ from that of differentiation?
-Integration is described as being more challenging than differentiation. While differentiation is a mechanical process of taking derivatives, integration involves finding the original function from its derivative, which can sometimes be very complex and even impossible to solve without a computer.
What is an anti-derivative and how is it related to integration?
-An anti-derivative is another term for an integral. It represents the process of finding a function whose derivative is the given function. In other words, it's the reverse operation of taking a derivative, aiming to recover the original function from which the derivative was taken.
What is the significance of the constant 'C' in the context of indefinite integrals?
-The constant 'C' in indefinite integrals signifies that there are infinitely many solutions to the integral. It represents an arbitrary constant that can be any number, emphasizing that the integral represents a family of functions that differ only by a constant value.
How does the process of integration relate to finding the area under a curve?
-Integration is directly related to finding the area under a curve. A definite integral represents the exact area under the curve between two specified points. By evaluating the antiderivative at the upper and lower bounds of the interval and subtracting, one can find the area enclosed by the curve and the x-axis.
What is the fundamental theorem of calculus and how does it relate to calculating the area under a curve?
-The fundamental theorem of calculus states that the definite integral of a function from point A to point B is equal to the antiderivative evaluated at point B minus the antiderivative evaluated at point A. This theorem is used to calculate the area under a curve by evaluating the integral at the endpoints of the interval and subtracting the results.
What is the basic formula for integrating a polynomial function of the form x^n?
-The basic formula for integrating a polynomial function of the form x^n is (1/(n+1)) * x^(n+1) + C, where n cannot be equal to -1. This formula is used to find the integral of any polynomial function by adding 1 to the exponent and dividing by the new exponent.
How does the process of integration handle constant factors in a function?
-When integrating a function that includes a constant factor, the constant can be taken out of the integral sign and multiplied by the result of the integration of the remaining function. This property mirrors the process of differentiation where constants are factored out before taking the derivative.
What is the integral of the cosine function and why?
-The integral of the cosine function is the sine function plus a constant. This is because the derivative of the sine function is the cosine, so integrating the cosine should yield the sine function, which is the original function before differentiation.
What is the concept of slicing a function into infinite slices to approximate the area under a curve?
-The concept involves dividing the area under the curve into an infinite number of infinitesimally small slices (rectangles), calculating the area of each slice (width times height), and summing these areas to approximate the total area under the curve. As the width of the slices (Δx) approaches zero, the summation becomes an integral, providing an exact representation of the area.
What are some applications of integrals in real-life scenarios?
-Integrals have numerous applications in engineering and physics, where they are used to calculate areas under curves that represent various physical quantities. They are essential for solving problems that involve accumulation of values over a range, such as work done in mechanics, electric charge accumulation, and volume calculations under curves.
Outlines
📚 Introduction to Derivatives and Integrals
The paragraph introduces the concepts of derivatives and integrals in calculus. It explains that taking derivatives involves using techniques like the chain rule and involves repeated application of these techniques until no more derivatives can be taken. Integration, on the other hand, is presented as a more challenging task, especially for certain types of integrals that may require a computer to solve. The speaker aims to provide a solid foundation for understanding these mathematical concepts and their applications in fields like engineering and physics.
🔄 Understanding Integrals and Anti-Derivatives
This section delves deeper into the concept of integrals, also known as anti-derivatives, which are the reverse process of taking derivatives. The speaker uses the analogy of finding a function that, when differentiated, yields a given function. The integral of a function is written with an 'S' symbol and involves integrating a function over a differential variable 'DX'. The concept of a constant (C) in integrals is introduced, signifying that there are infinitely many solutions to an integral, all differing by a constant.
📈 Basic Rules and Properties of Integrals
The speaker outlines the basic rules for integrating polynomial functions, such as dividing the exponent by 'n' and adding one to find the exponent of the integrated function. Special attention is given to the exclusion of 'n' being equal to '-1'. The paragraph also covers the property that allows constants to be factored out of the integral, similar to how constants are handled in differentiation. The importance of these properties for solving integral problems is emphasized.
📊 Combining Functions and Integration
This paragraph discusses the property of integration that allows for the easy combination of multiple functions into a single integral. The speaker explains that if you have two functions, f(x) and g(x), their combined integral is simply the sum of their individual integrals. This is demonstrated with an example involving the integral of a sum of two polynomial functions, where each term is integrated separately and then added together, along with their respective constants.
🌐 Trigonometric Integrals
The speaker shifts focus to trigonometric integrals, providing a list of integrals for common trigonometric functions. The integral of the sine function is the cosine function, the integral of the cosine function is the sine function, and similar relationships are established for tangent, secant, and cotangent functions. The speaker emphasizes that these relationships can be derived from the list of derivatives previously discussed, and that understanding these integrals is crucial for solving calculus problems involving trigonometric functions.
🏞️ The Meaning of Integrals: Area Under a Curve
The speaker explains that integrals have a geometric interpretation as the area under a curve. A definite integral represents the area bounded by the curve and the x-axis between two points on the x-axis. The process of calculating this area is likened to summing the areas of infinitesimally small rectangles under the curve. The fundamental theorem of calculus is introduced, which states that the definite integral of a function from point A to point B is equal to the antiderivative evaluated at point B minus the antiderivative evaluated at point A.
📐 Practical Applications of Integrals: Area Calculation
The final paragraph discusses the practical application of integrals in calculating areas of shapes that cannot be easily defined by traditional geometric formulas, such as curves. The speaker explains that by defining a shape as a function, its area can be determined using integral calculus. This method is applicable to a wide variety of shapes, including those that are complex or irregular. The speaker also mentions that all basic area formulas, such as those for triangles and squares, can be derived using calculus.
Mindmap
Keywords
💡Derivatives
💡Integrals
💡Chain Rule
💡Anti-Derivative
💡Differential Variable (dx)
💡Constant of Integration (C)
💡Definite Integral
💡Indefinite Integral
💡Fundamental Theorem of Calculus
💡Trigonometric Functions
Highlights
Derivatives and integrals are fundamental concepts in calculus, with derivatives representing the slope of a curve at a given point, while integrals represent the area under a curve.
The process of taking a derivative involves using various rules such as the chain rule, multiplication rule, and division rule, essentially multiplying everything together as you move inward through the function.
Integration is more challenging than differentiation, especially for more complex functions, and sometimes requires the use of a computer to solve.
The concept of an integral as the area under a curve is introduced using an analogy with derivatives, where the goal is to find a function that, when differentiated, yields the original function.
The indefinite integral is a general problem without definite bounds, represented by the integral symbol with no numbers on top or bottom, and always includes an arbitrary constant 'C'.
The definite integral, on the other hand, has numbers on the integral symbol indicating specific bounds, and is used to calculate the exact area under a curve between those bounds.
The fundamental theorem of calculus states that the definite integral of a function from A to B is equal to the antiderivative of the function evaluated at B minus the antiderivative evaluated at A.
The process of calculating a definite integral involves slicing the function into infinitesimally small parts (slices), calculating the area of each slice, and summing these areas to find the total area under the curve.
Integration by parts and properties such as constant multiplication and function addition are discussed, providing a foundation for solving integrals of polynomials and trigonometric functions.
The integral of a function can be thought of as the limit of the sum of the areas of infinitesimally small rectangles under the curve, which is the fundamental definition of an integral.
The concept of integration is not only useful in theoretical mathematics but also has practical applications in fields like engineering and physics.
The transcript provides a detailed explanation of how to calculate the area under a curve using integration, which is a powerful tool for solving real-world problems involving shapes and volumes.
The relationship between derivatives and integrals is emphasized, with the latter being the reverse process of the former, and both playing crucial roles in understanding the behavior of functions.
The transcript introduces the concept of the antiderivative, which is another term for an integral, highlighting its importance in calculus and its connection to finding the original function from its derivative.
The process of integration is likened to summing the areas of infinitesimally small rectangles, providing a visual and intuitive understanding of how the integral represents the area under a curve.
The transcript explains the importance of the constant 'C' in integrals, which accounts for the infinite number of possible antiderivatives that can derive the same derivative.
The transcript outlines the basic rules for integrating polynomials and trigonometric functions, providing a foundation for more complex integration problems.
The concept of integration is used to calculate the area of shapes that cannot be easily determined using traditional geometric formulas, such as those with curved boundaries.
The transcript emphasizes the importance of understanding both the theoretical and practical aspects of integration, as it is a key tool in advanced mathematical studies and applications.
Transcripts
Browse More Related Video
Antiderivatives and Indefinite Integrals

Calculus AB/BC – 6.7 The Fundamental Theorem of Calculus and Definite Integrals
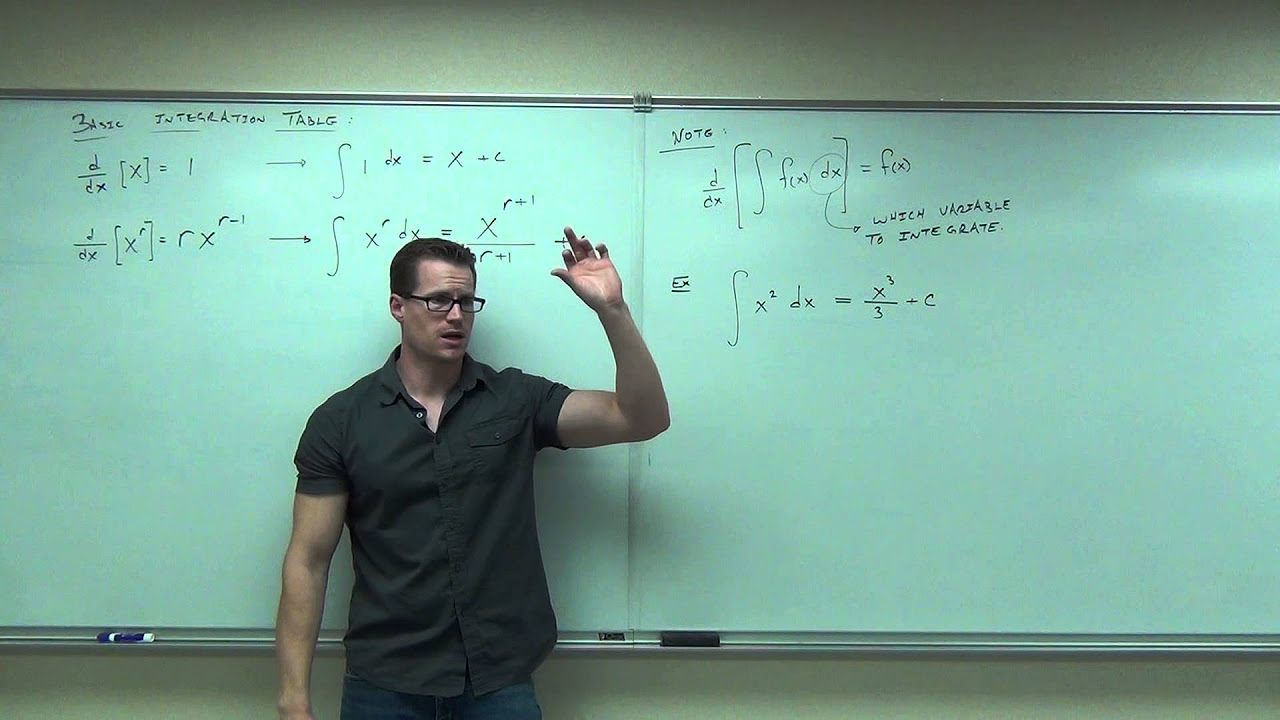
Calculus 1 Lecture 4.1: An Introduction to the Indefinite Integral

What is Calculus? (Mathematics)
AP Calculus AB Review

Calculus AB/BC – 6.4 The Fundamental Theorem of Calculus and Accumulation Functions
5.0 / 5 (0 votes)
Thanks for rating: