College Physics 1: Lecture 12 - Projectile Motion

Spahn's Science Lectures

23 Sept 202049:06

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture introduces the concept of projectile motion, explaining it as a two-dimensional motion influenced solely by gravity, resulting in parabolic trajectories. The instructor defines a projectile and emphasizes that horizontal and vertical motions are independent, unaffected by initial horizontal velocity. Kinematic equations are adapted for projectile motion, simplifying them by setting horizontal acceleration to zero and vertical acceleration to -g (9.8 m/s^2). Through examples, the lecture demonstrates how to calculate flight time and muzzle velocity, illustrating the problem-solving process for projectile motion. The video also clarifies misconceptions regarding the effect of mass on falling objects, showing that all objects fall at the same rate in the absence of air resistance.

Takeaways

📝 Projectile motion is a two-dimensional extension of free-fall motion, influenced only by gravity.
🌍 Air resistance is ignored in these problems for simplicity, as it has minimal effect on dense objects moving at moderate speeds.
🔄 All projectiles follow a parabolic path due to the influence of gravity.
⚖️ The horizontal and vertical motions of a projectile are independent of each other.
🏀 The vertical motion of a projectile is the same as free-fall motion, affected only by gravity.
📉 The horizontal acceleration of a projectile is zero, meaning its horizontal velocity remains constant.
🔍 Key equations for projectile motion are derived from kinematic equations, modified to account for the lack of horizontal acceleration and the constant vertical acceleration due to gravity.
🎯 Problem-solving in projectile motion involves breaking down vectors into components and applying kinematic equations separately to the horizontal and vertical motions.
🔄 Projectile motion exhibits symmetry; the speed at which a projectile rises is the same as the speed at which it falls at equivalent heights.
📐 Solving projectile motion problems requires careful consideration of initial conditions, vector components, and the application of kinematic equations to find unknown quantities such as time of flight and horizontal distance.

Q & A

What is a projectile?
-A projectile is an object that moves in two dimensions and is only under the influence of gravity, without considering air resistance.
Why is air resistance ignored in projectile motion problems?
-Air resistance is ignored to simplify calculations, as its effect is minimal for reasonably dense objects moving at modest speeds.
What path does a projectile follow?
-A projectile follows a parabolic path.
How are the horizontal and vertical motions of a projectile related?
-The horizontal and vertical motions of a projectile are independent of one another.
What happens to the horizontal velocity of a projectile during its flight?
-The horizontal velocity of a projectile remains constant because there is no horizontal acceleration.
What is the acceleration of a projectile in the vertical direction?
-The acceleration in the vertical direction is due to gravity, which is -9.8 meters per second squared.
How can the kinematic equations be adapted for projectile motion?
-The kinematic equations for projectile motion are the same as those for one-dimensional motion, with the horizontal acceleration set to zero and the vertical acceleration set to -g.
What is the significance of the symmetry in projectile motion?
-The motion is symmetrical about the highest point, meaning the projectile has the same speed when moving upwards and downwards at the same heights.
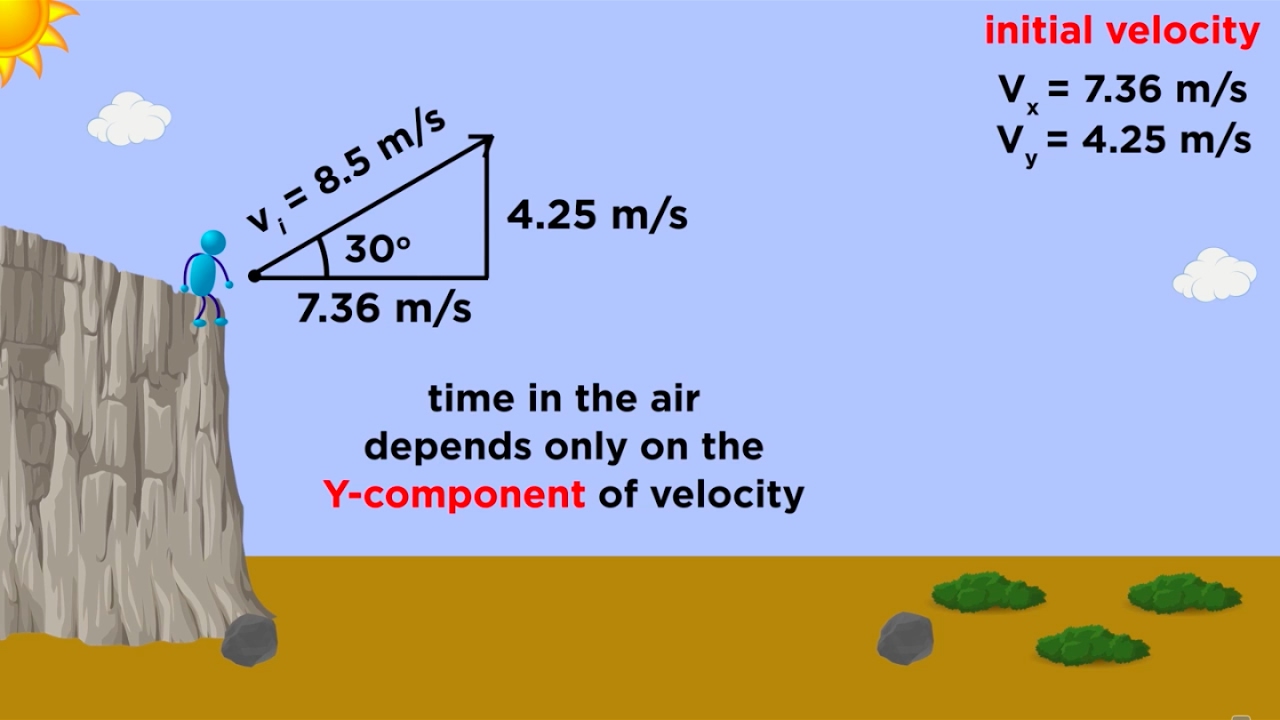
How do you determine the initial velocity components of a projectile?
-The initial velocity components are determined using trigonometric functions: Vx = V * cos(θ) and Vy = V * sin(θ), where V is the initial velocity and θ is the angle of projection.
How does the example of the falling balls demonstrate the independence of vertical and horizontal motions?
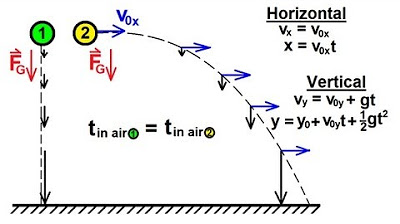
-The example shows that a ball released from rest and a ball shot horizontally both hit the ground simultaneously, illustrating that vertical motion is unaffected by horizontal motion.

Outlines

00:00

🚀 Introduction to Projectile Motion

The lecture begins with an introduction to projectile motion, explaining it as a two-dimensional motion influenced solely by gravity. Examples such as balls flying through the air and cars performing stunts are given. The lecturer emphasizes that while air resistance is typically present, it is negligible for dense objects moving at moderate speeds, thus it is ignored for simplicity. The path of a projectile, a parabolic trajectory, is introduced, and the concept that projectile motion problems can be solved by developing a framework for these types of problems is highlighted.

05:00

📚 Fundamental Concepts of Projectile Motion

This section delves into the definitions and framework necessary to understand and solve projectile motion problems. The independence of horizontal and vertical motions is discussed, with a strobe photograph demonstration provided to illustrate that the vertical motion is identical for both freely falling and horizontally projected objects. The讲师 emphasizes that the horizontal motion is uniform and unaccelerated, while the vertical motion is under the influence of gravity, leading to an acceleration of -9.8 m/s² downwards. The symmetry in the motion of projectiles is also highlighted.

10:00

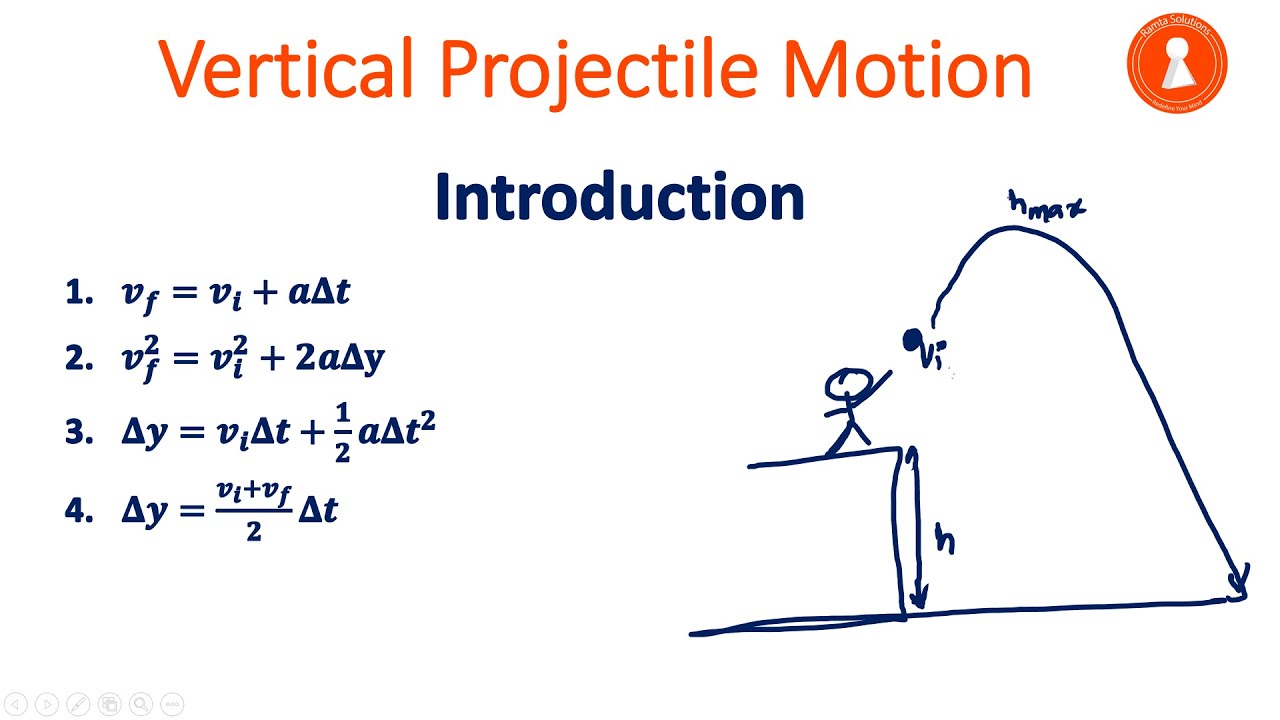
📉 Kinematic Equations for Projectile Motion

The lecturer presents the kinematic equations for projectile motion, modifying the standard equations to account for the absence of horizontal acceleration and the presence of vertical acceleration due to gravity. The horizontal velocity remains constant (vx_final = vx_initial), and the vertical velocity changes due to gravity (vy_final = vy_initial - g*Δt). The position equations are also adapted for projectile motion, with the讲师 demonstrating how to simplify them by substituting the known accelerations.

15:02

🔍 Solving Projectile Motion Problems

The lecture continues with an example problem involving a rifle aiming at a target. The讲师 guides through the process of setting up the problem by identifying known positions, velocities, and accelerations, and what is being sought: the bullet's flight time and muzzle velocity. The讲师 uses the vertical position equation to solve for the time of flight and then the horizontal position equation to find the initial horizontal velocity. The overall muzzle velocity is then calculated using the Pythagorean theorem, considering both the horizontal and vertical components of the initial velocity.

20:04

🎯 Complex Projectile Motion Scenario: The Bus Jump

An in-depth example is presented where a bus must maintain a speed above 50 miles per hour to avoid exploding, and it must clear a 50-foot gap in a freeway overpass while traveling at an angle of 5 degrees. The讲师 performs unit conversions from miles per hour to meters per second and from feet to meters. The initial velocity components are calculated using trigonometric functions. The讲师 then sets up the equations for both the horizontal and vertical motions to determine if the bus can make the jump, highlighting the process of solving for time and horizontal distance using the projectile motion equations.

25:06

📚 Summary of Projectile Motion Principles

The lecture concludes with a summary of the principles of projectile motion. The讲师 reviews the independence of horizontal and vertical motions, the constant horizontal velocity, and the accelerated vertical motion due to gravity. Two quick questions are posed to the students to reinforce the concepts: one about which ball hits the ground first when released from rest at different heights and projected horizontally, and another about the distance two balls of different masses roll off a table and land, emphasizing that the mass does not affect the horizontal distance traveled in the absence of air resistance.

Mindmap

Keywords

💡Projectile Motion

Projectile motion refers to the movement of an object through two dimensions under the influence of gravity alone. It is a fundamental concept in physics that allows for the analysis of objects in free fall or those that are thrown or projected. In the video, projectile motion is the central theme, with examples such as balls flying through the air and stunt jumps by cars. The script explains that projectile motion follows a parabolic path, which is a key point in understanding the physics of such movements.

💡Free-Fall Motion

Free-fall motion is a type of motion experienced by an object when it is solely under the influence of gravity, without any other forces acting upon it, such as air resistance. In the context of the video, free-fall motion is an extension to one dimension of what is experienced in projectile motion, which is two-dimensional. The script uses free-fall motion to build upon and explain the more complex scenarios of projectile motion.

💡Air Resistance

Air resistance, also known as drag, is the force that opposes an object's motion through a fluid like air. While real objects are influenced by air resistance, the video script simplifies the problems by ignoring it, assuming that the objects are dense and moving at modest speeds where the effect of air resistance is minimal. This simplification allows for clearer explanations and problem-solving in the context of projectile motion.

💡Parabolic Path

A parabolic path is the trajectory followed by an object in projectile motion. It is characterized by an initial upward curve followed by a descent back to the ground, forming a U-shape when viewed from the side. In the video, the parabolic path is used to describe the shape of the trajectory that projectiles follow, which is crucial for visualizing and calculating the motion of objects in two dimensions.

💡Horizontal and Vertical Motion Independence

In projectile motion, the horizontal and vertical components of motion are independent of each other. This means that the horizontal motion does not affect the vertical motion and vice versa. The video script illustrates this concept with a strobe photograph of two falling balls, showing that the vertical motions are identical despite the horizontal motion of one of the balls. This principle is essential for solving projectile motion problems.

💡Acceleration Due to Gravity

Acceleration due to gravity is the constant acceleration that objects experience when in free fall, directed vertically downward. With a magnitude of approximately 9.8 m/s² on Earth, it is a key factor in calculating the vertical component of projectile motion. The video script emphasizes that the only acceleration acting on projectiles is gravity, which always points downward, affecting the vertical motion but not the horizontal.

💡Kinematic Equations

Kinematic equations are mathematical formulas used to describe the motion of objects. In the context of the video, these equations are adapted for projectile motion by incorporating the specific accelerations in the horizontal and vertical directions. The script explains how the standard kinematic equations are modified to account for the absence of horizontal acceleration and the presence of gravity-induced vertical acceleration.

💡Muzzle Velocity

Muzzle velocity is the speed of a projectile at the moment it leaves the muzzle of a firearm. In the video, the script uses the concept of muzzle velocity in the context of calculating the initial velocity of a bullet fired from a rifle, which is essential for determining the bullet's trajectory and flight time.

💡Unit Conversions

Unit conversions are necessary when dealing with different measurement systems, such as converting miles per hour to meters per second or feet to meters. The video script includes unit conversions as part of the problem-solving process, demonstrating the importance of using consistent and appropriate units for the calculations involved in projectile motion.

💡Trigonometric Functions

Trigonometric functions, such as sine and cosine, are used to break down the initial velocity vector into its horizontal and vertical components. In the video, the script applies these functions to determine the x and y components of the initial velocity of a bus in a scenario where it must jump a gap. Understanding the application of trigonometric functions is crucial for analyzing projectile motion in two dimensions.

Highlights

Introduction to projectile motion as a two-dimensional extension of free-fall motion.

Definition of a projectile as an object moving in two dimensions solely under the influence of gravity, ignoring air resistance for simplicity.

Explanation of the parabolic path followed by projectiles due to their two-dimensional motion.

The independence of horizontal and vertical motions in projectile motion, demonstrated through a strobe photograph of two falling balls.

Horizontal motion of projectiles remains constant with no acceleration, while vertical motion is influenced by gravity.

The kinematic equations for projectile motion, adapted from the basic equations used in simpler motion scenarios.

Solving projectile motion problems by establishing equations for horizontal and vertical components separately.

Example problem involving a rifle bullet's flight time and muzzle velocity, demonstrating the application of projectile motion equations.

Step-by-step problem-solving strategy for projectile motion, including drawing a picture, writing down knowns and unknowns, and using equations.

Conversion of units as a necessary step in solving projectile motion problems, such as converting miles per hour to meters per second.

Breaking down the initial velocity vector into horizontal and vertical components using trigonometric functions.

The concept of symmetry in projectile motion, where the upward and downward motions are mirror images.

A real-world scenario involving a bus jumping a gap in a freeway overpass, illustrating the practical application of projectile motion principles.

Determination of whether the bus in the scenario will successfully make the jump based on its initial velocity and the gap's width.

The significance of mass in projectile motion, stating that it does not affect the rate of fall due to gravity.

Conclusion of the lecture with a transition to the next section on forces, which cause motion.

Transcripts

Browse More Related Video

Physics 3: Motion in 2-D Projectile Motion (1 of 21) Independent Motion in x and y

AP Physics - Projectile Motion

Vertical Projectile Motion: Introduction and Terminology

Kinematics Part 3: Projectile Motion

Using Equations of Projectile Motion

introduction to projectile motion

Related Tags

Projectile Motion Physics Lecture Parabolic Path Free-Fall Motion Horizontal Motion Vertical Motion Motion Independence Kinematic Equations Problem Solving Educational Content