Solving Projectile Motion Problems in Physics - [1-4-7]
TLDRThis lesson delves into projectile motion, specifically horizontal and vertical components. It begins with sketching the parabolic trajectory of a ball thrown horizontally from a 20-meter building, emphasizing the separation of horizontal and vertical motions. The equations of motion are introduced, highlighting their application in both directions. The lesson then demonstrates how to graph the x and y components of velocity over time, showing that the horizontal velocity remains constant while the vertical velocity increases quadratically due to gravity. Finally, it calculates the horizontal distance from the building where the ball lands, using the vertical motion to determine the time in air and the horizontal motion to find the distance. The key takeaway is that the horizontal speed does not affect the time to hit the ground, only the distance traveled horizontally.
Takeaways
- 📌 Projectile motion can be analyzed by separating horizontal and vertical components.
- 🏌️ In horizontal motion, there is no acceleration (air resistance is neglected), leading to a linear relationship with time.
- 📉 For vertical motion, the only acceleration is due to gravity, which results in a quadratic relationship with time.
- 🚀 The initial horizontal velocity of the ball is 5.0 m/s from the top of a 20-meter building.
- 📈 The trajectory of the ball is parabolic, with the shape being quadratic and upside-down due to the acceleration of gravity.
- 🎯 The x-component of the ball's velocity remains constant because there is no horizontal acceleration.
- 🔽 The y-component of the ball's velocity increases linearly with time due to the downward acceleration of gravity.
- 🕒 The time it takes for the ball to hit the ground is independent of the horizontal velocity and depends solely on the height from which it is thrown and gravity.
- 📍 The ball will land at a distance of 10.1 meters from the base of the building.
- 🔄 The principles of projectile motion apply to all objects thrown horizontally, regardless of their initial horizontal velocity.
- 🧠 Understanding the separate equations for horizontal and vertical motion is crucial for solving projectile motion problems.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is projectile motion, specifically focusing on solving problems related to a ball tossed horizontally from a height with an initial velocity.
How many parts are there in the projectile motion problem discussed in the transcript?
-There are four parts in the projectile motion problem: sketching the path of the trajectory, graphing the x component of velocity as a function of time, graphing the y component of velocity as a function of time, and determining the distance from the foot of the building where the ball lands.
What is the initial horizontal velocity of the ball mentioned in the problem?
-The initial horizontal velocity of the ball is 5.0 meters per second.
What is the height of the building from which the ball is tossed?
-The ball is tossed from the top of a 20-meter tall building.
How does the horizontal motion of the ball affect the time it takes to hit the ground?
-The horizontal motion of the ball does not affect the time it takes to hit the ground. The time it takes for the ball to hit the ground is determined solely by the vertical motion and the height from which it is dropped.
What is the general form of the equation of motion used in the x direction?
-The general form of the equation of motion used in the x direction is v = v₀ + a*t, where v is the final velocity, v₀ is the initial velocity, a is the acceleration, and t is the time.
What is the general form of the equation of motion used in the y direction?
-The general form of the equation of motion used in the y direction is y = y₀ + v₀*t + 0.5*a*t², where y is the final position, y₀ is the initial position, v₀ is the initial velocity, a is the acceleration (which is negative due to gravity), and t is the time.
What is the shape of the trajectory of the ball according to the equations of motion?
-The shape of the trajectory of the ball is a parabola, specifically an upside-down parabola, as determined by the equations of motion.
How is the x component of the ball's velocity affected by time?
-The x component of the ball's velocity remains constant over time because there is no acceleration in the horizontal direction. It is always equal to the initial horizontal velocity.
How is the y component of the ball's velocity affected by time?
-The y component of the ball's velocity increases linearly with time due to the acceleration caused by gravity. It is given by the equation v_y = -9.8*t, where v_y is the vertical velocity and t is the time.
What is the distance from the foot of the building where the ball lands?
-The ball lands at a distance of 10.1 meters from the foot of the building, as calculated by substituting the time it takes for the ball to hit the ground (2.02 seconds) into the horizontal motion equation (x = 5*t).
Outlines
📚 Introduction to Projectile Motion
The lesson begins with an introduction to projectile motion, emphasizing the importance of understanding the equations of motion for both horizontal and vertical components. The problem presented involves a ball thrown horizontally from the top of a 20-meter building with an initial velocity of 5.0 m/s. The goal is to sketch the trajectory, graph the velocity components, and determine the landing distance. The lesson highlights the separation of horizontal and vertical motions and the significance of part A in understanding the rest of the problem.
📈 Trajectory and Velocity Components
This paragraph delves into the specifics of the ball's trajectory and its velocity components. The focus is on sketching the path of the ball and understanding the separate motions in the x (horizontal) and y (vertical) directions. The equations of motion are introduced, with the x-component being linear in time and the y-component being quadratic. The explanation includes the absence of horizontal acceleration and the presence of gravitational acceleration in the vertical direction, leading to a parabolic trajectory. The mathematical proof of the parabolic shape is discussed, reinforcing the initial sketch with a deeper understanding.
🏃♂️ Constant Horizontal Velocity
The third paragraph discusses the constant horizontal velocity of the ball. It explains that in the absence of horizontal acceleration, the horizontal velocity remains unchanged throughout the motion. The equation of motion for the x-component of velocity is simplified to show that it is a constant value, which is the initial velocity. This results in a constant horizontal speed, meaning the ball travels the same distance horizontally every second. The concept is illustrated with a graph showing a horizontal line representing the constant velocity over time.
📉 Increasing Vertical Velocity
This section focuses on the vertical component of the ball's velocity, which increases over time due to gravity. The initial vertical velocity is zero, and the acceleration is due to gravity, represented as -9.8 m/s². The equation of motion for the y-component of velocity is used to describe the increasing speed as time progresses. A graph is sketched to illustrate the linear increase in downward velocity over time, starting from zero at the moment of release and accelerating downwards with each passing second.
🏁 Determining Landing Distance
The paragraph outlines the process of calculating the distance from the base of the building where the ball lands. It explains the strategy of using the vertical motion equation to determine the time it takes for the ball to hit the ground (2.02 seconds) and then using this time to calculate the horizontal distance using the constant horizontal velocity. The final result is a landing distance of 10.1 meters, demonstrating that the horizontal motion is independent of the time it takes to hit the ground, which is solely determined by the height from which the ball is dropped and the acceleration due to gravity.
🎯 Summary and Future Lessons
The final paragraph serves as a summary of the lesson and a preview for future topics. It reiterates the key concepts learned, such as the separation of horizontal and vertical motions and the equations of motion. The lesson provides a roadmap for solving projectile motion problems and encourages practice and further study. It ends with a prompt to continue to the next lesson, where the skills learned will be further developed and applied.
Mindmap
Keywords
💡Projectile Motion
💡Horizontal Velocity
💡Vertical Motion
💡Acceleration
💡Trajectory
💡Equations of Motion
💡Graphs
💡Parabolic Path
💡Free Fall
💡Time of Flight
💡Distance from Building
Highlights
The lesson focuses on projectile motion, specifically addressing a problem involving a ball thrown horizontally from a 20-meter building.
The initial horizontal velocity of the ball is 5.0 meters per second.
The ball is considered to have no initial vertical velocity component.
The equations of motion are derived and applied separately to the horizontal (x) and vertical (y) directions.
The horizontal motion is described by a linear equation in time, as there is no horizontal acceleration.
The vertical motion is described by a quadratic equation in time due to the acceleration of gravity.
The trajectory of the ball is parabolic, with the shape confirmed mathematically to be quadratic.
The x-component of the ball's velocity remains constant at 5.0 m/s, as there is no horizontal acceleration.
The y-component of the ball's velocity increases linearly with time due to gravity, starting at zero initial velocity.
The ball will hit the ground after 2.02 seconds, regardless of its horizontal velocity.
The horizontal distance from the building where the ball lands is calculated to be 10.1 meters.
The lesson emphasizes the independence of horizontal and vertical motions in projectile problems.
The method for solving projectile motion problems is outlined, emphasizing the separation of x and y components and the use of equations of motion.
The lesson concludes by encouraging practice and reiteration of the problem-solving process for better understanding.
Transcripts
Browse More Related Video
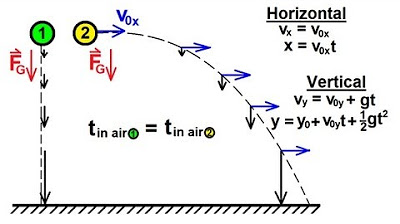
Physics 3: Motion in 2-D Projectile Motion (1 of 21) Independent Motion in x and y

Horizontally launched projectile | Two-dimensional motion | Physics | Khan Academy

Physics 3.5.4a - Projectile Practice Problem 1

AP Physics 1 Workbook 1.N Projectile Motion Part 2 Solution
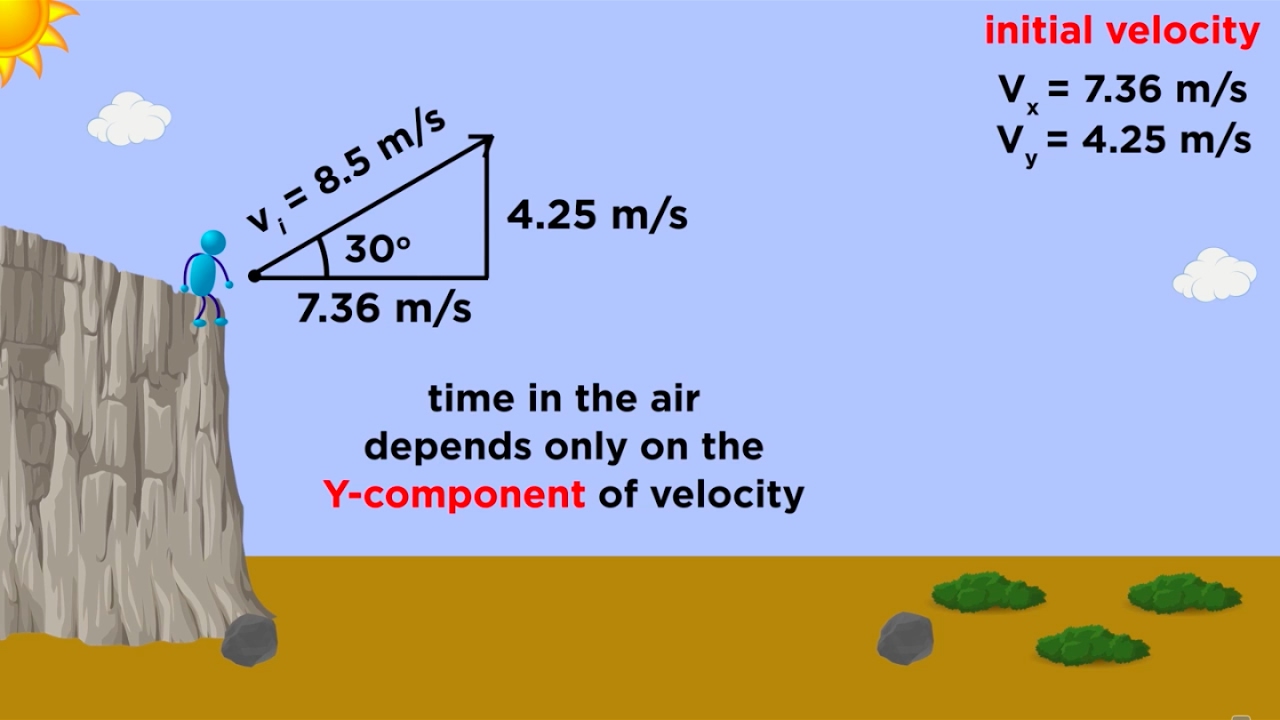
Kinematics Part 3: Projectile Motion

AP Physics B Kinematics Presentation General Problems #10
5.0 / 5 (0 votes)
Thanks for rating: