Derivatives... What? (NancyPi)
TLDRThe video script provides an in-depth explanation of the concept of a derivative in calculus, emphasizing its role in determining the slope or rate of change at any point on a curve. It introduces the formal definition of a derivative using limits and illustrates the process of finding the derivative through the limit process. The script simplifies the concept by comparing it to the slope of a tangent line at a point on a curve and highlights the practical application in physics. It concludes by mentioning that while the limit process is foundational, there are more efficient methods, such as derivative rules, for calculating derivatives in practice.
Takeaways
- 📚 The derivative is a function that represents the slope of the tangent line to a curve at any given point, indicating the rate of change or instantaneous rate of change.
- 🔍 To define the derivative, we use the concept of limits, which helps in finding the exact slope at a point by narrowing down the distance between two points on the curve as they approach each other.
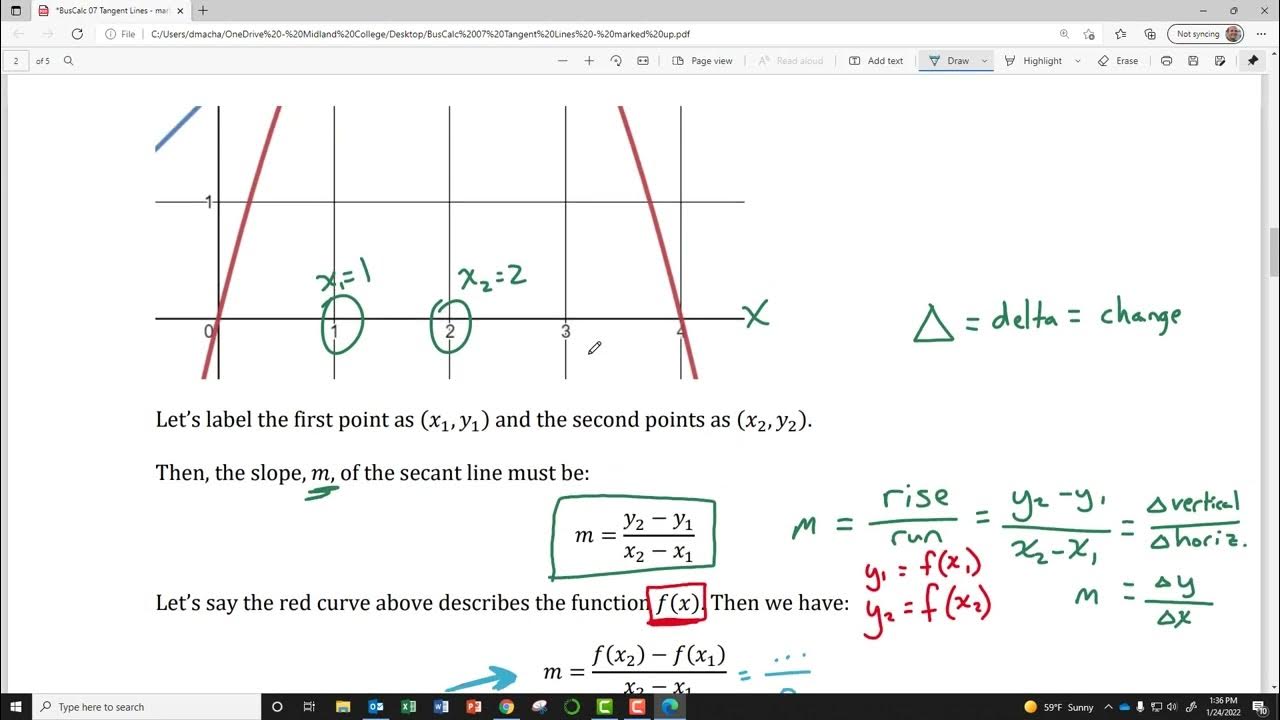
- 📈 The slope formula (rise over run) is fundamental in calculating the secant line's slope, which serves as an approximation for the tangent line's slope before taking the limit as h approaches zero.
- 🤔 The derivative is a variable slope because it can change at different points on the curve, which is why it is represented as a function, f'(x), similar to the original function f(x).
- 🌟 The process of finding the derivative involves algebraic manipulation and simplification, including distributing, factoring, and canceling terms to isolate the variable as h approaches zero.
- 🎯 The derivative of a function, such as 3x^2 + 12, can be found by applying the limit process, resulting in a simpler expression, in this case, 6x, which represents the slope at any point on the curve.
- 🚀 Understanding the concept of derivatives is crucial in fields like physics, where it can represent velocity and acceleration in motion-related problems, highlighting changes in speed and direction over time.
- 📝 While the limit process is a valid and illustrative method for finding derivatives, it can be tedious and involves extensive algebra; thus, in practice, other methods like derivative rules are often used for efficiency.
- 🛠️ The derivative rules provide a faster and simpler way to calculate derivatives, reducing the need for complex algebraic steps, and are the preferred approach in most mathematical applications.
- 💡 The video script serves as an educational resource for those looking to understand the concept of derivatives and the process of finding them using the definition and limit process.
Q & A
What is the main concept Nancy is introducing in the video?
-Nancy is introducing the concept of a derivative, explaining it as a function that tells you the slope of the tangent line to a curve at any point, which represents the rate of change or the instantaneous rate of change at that point.
How does Nancy describe the tangent line to a curve?
-Nancy describes the tangent line as a line that touches the curve at only one point, skimming or grazing the surface of the curve without crossing it elsewhere.
What is the challenge in finding the slope of the tangent line?
-The challenge is that we only know one point for sure on each tangent line, and we need two points to calculate the slope using the standard slope formula.
How does Nancy propose to overcome the challenge of finding the slope of the tangent line?
-Nancy suggests using the slope of a secant line as an approximation for the tangent line's slope, and then taking the limit as the horizontal distance (h) between the two points approaches zero, which refines the approximation to the exact slope of the tangent line.
What is the definition of the derivative according to Nancy?
-The definition of the derivative, according to Nancy, is the limit of the secant line's slope as the distance (h) between the two points on the curve approaches zero, which gives the slope of the tangent line at a specific point on the curve.
How does the derivative relate to the rate of change?
-The derivative represents the instantaneous rate of change at any point on the curve, providing a measure of how quickly the value of the function is changing at that specific point.
What is the practical application of derivatives mentioned in the script?
-The practical application of derivatives mentioned in the script is in physics, where the derivative can be used to determine the velocity of an object, which is changing over time, and the acceleration, which is the rate of change of velocity.
What is the recommended method for finding derivatives in practice?
-In practice, Nancy recommends using derivative rules instead of the limit process for finding derivatives, as it is faster and involves less algebra.
What is the result of finding the derivative of the function 3x^2 + 12?
-The result of finding the derivative of the function 3x^2 + 12 is 6x, which means the slope of the tangent line at any point on the curve is given by the number 6x.
How does Nancy encourage the viewers to engage with her content?
-Nancy encourages viewers to engage with her content by asking them to click 'Like' or subscribe if they found the video helpful or enjoyable.
What is the significance of the limit process in the definition of the derivative?
-The limit process is significant in the definition of the derivative because it allows us to refine our approximation of the slope of the tangent line to the exact value, making the derivative a precise measure of the rate of change at a specific point on the curve.
Outlines
📚 Introduction to Derivatives
This paragraph introduces the concept of derivatives, explaining it as a function that reveals the slope of the tangent line to a curve at any given point. It emphasizes the derivative's role in determining the instantaneous rate of change. The video promises a step-by-step explanation to make the concept accessible, even to those who might initially find it intimidating. The paragraph also touches on the idea of using limits to define the derivative and suggests that viewers can jump ahead for the calculation part if they prefer.
📈 Understanding the Secant and Tangent Lines
This section delves deeper into the geometric interpretation of derivatives by discussing secant and tangent lines. It explains that the derivative at a point is equivalent to the slope of the tangent line at that point on the curve. The paragraph illustrates the process of moving from an approximation of the slope using a secant line to finding the exact slope of the tangent line by taking the limit as the horizontal distance (h) approaches zero. This process refines the estimate of the slope, transforming the secant line into the tangent line, and ultimately leading to the definition of the derivative.
🧮 Calculating Derivatives Using the Limit Process
In this part, the video script outlines the method of calculating derivatives using the limit process. It describes how to apply the definition of the derivative to a given function by substituting x with x + h in the function and then taking the limit as h approaches zero. The paragraph provides a step-by-step guide on how to perform the algebraic manipulations required to find the derivative, using an example to demonstrate the process. It concludes with a reminder that while this method is illustrative, it can be tedious in practice, and there are faster and simpler methods available for finding derivatives.
Mindmap
Keywords
💡derivative
💡slope
💡tangent line
💡limit
💡secant line
💡rate of change
💡instantaneous rate of change
💡function
💡algebra
💡derivative rules
💡calculus
Highlights
Derivative is a function that tells you the slope of the tangent line at any point on a curve, representing the rate of change at any instant.
The derivative can be understood as the instantaneous rate of change at any point on a curve.
A tangent line is a line that touches the curve at only one point, and every point on the graph has a different tangent line.
To find the slope of the tangent line, one must deal with the challenge of knowing only one point on the tangent line.
The slope of a straight line can be found using the slope formula, but this is not directly applicable to the changing slope of a curve.
The slope of the secant line, which connects two points on the curve, serves as an approximation for the slope of the tangent line.
The difference quotient is the slope of the secant line, given by the formula (f(x + h) - f(x)) / h.
To find the exact slope, one can take the limit as h approaches zero, making the secant line's slope equal to the tangent line's slope.
The limit of the secant line's slope as h approaches zero is the definition of the derivative.
The derivative is a function itself, reflecting the variable slope of the tangent line at different points on the curve.
The derivative can be calculated using the definition with the limit process, although this method can be tedious.
In practice, derivative rules provide a faster and simpler way to find the derivative, reducing the need for extra algebra.
The derivative has practical applications in fields like physics, where it can represent changing velocities and accelerations.
The derivative of the function 3x^2 + 12 is 6x, meaning the slope of the function at any instant is given by 6x.
For those interested in learning more, there are additional resources such as videos on derivative rules available.
Understanding the concept of derivatives is essential, even if one does not necessarily enjoy math.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: