Calculus Symbols and Notation – Basic Introduction to Calculus
TLDRThe video introduces basic calculus notation and aims to demystify the subject for beginners. It explains the concept of integration as finding the area under a curve, using the function 3x^2 as an example. The video emphasizes that calculus, while challenging, is accessible with the right approach and understanding of its practical applications in everyday life and technology. The speaker, John, also promotes his math education resources for further learning.
Takeaways
- 📚 Introduction to calculus notation aims to demystify the subject for beginners, even those with no prior mathematical knowledge.
- 🌟 Calculus is a powerful mathematical tool with widespread applications in technology and modern life.
- 📈 The video focuses on basic calculus concepts, such as the elongated 'S' which represents the sum or integration of a function over an interval.
- 📊 Functions in mathematics are represented by symbols and have associated graphs; for example, 3x^2 is a specific function with a parabolic graph.
- 🤔 The main goal of the video is to help viewers understand the basic notation and symbols used in calculus, such as the elongated 'S' and 'dx'.
- 📐 The x-axis boundaries (like 2 and 5) are used to define the interval over which the integration or summation is performed.
- 🔍 Integration in calculus involves finding the area under a curve, which can be estimated by summing up infinitesimally small rectangles under the graph.
- 📚 Learning calculus involves understanding and applying specific rules and procedures to find precise areas or derivatives.
- 👨🏫 The speaker, John, is a math teacher and founder of Taba Class Math, offering online math courses and resources for various levels and exam preparations.
- 📝 The importance of taking good math notes is emphasized as a key to success in mathematics.
- 🚀 The video encourages viewers to explore calculus further and offers resources for those interested in learning more about the subject.
Q & A
What is the main purpose of the video?
-The main purpose of the video is to introduce basic calculus notation and demystify some of the symbols used in calculus for beginners or those who are interested in learning about it.
Who is the speaker in the video and what is his profession?
-The speaker in the video is John, the founder of Taba Class Math and a middle and high school math teacher.
What does the elongated 'S' symbol represent in calculus?
-The elongated 'S' symbol, also known as the integral sign, represents the process of integration in calculus, which involves finding the sum or the area under a curve.
What is a function in mathematics according to the video?
-A function in mathematics is a rule that assigns a unique output to each input and is represented by a symbol followed by a variable, such as 3x^2 which is a specific function.
How does the speaker describe the process of finding the area under a curve?
-The speaker describes the process of finding the area under a curve as adding up or integrating the values between two points on the x-axis, in this case, from 2 to 5, using the function's graph.
What is the significance of the 'dx' in calculus notation?
-The 'dx' in calculus notation is related to another important concept in calculus called the derivative. For the purpose of the problem discussed in the video, it is part of the integral notation indicating a small, infinitesimally small, change in the x variable.
How does the speaker simplify the concept of integration for beginners?
-The speaker simplifies the concept of integration by comparing it to adding up the areas of skinny rectangles placed under the curve of a function, ultimately aiming to find the exact area under the curve as the rectangles become infinitely thin.
What does the speaker suggest is the key to handling calculus?
-The speaker suggests that the key to handling calculus is learning the specific rules and procedures that calculus provides, along with understanding the practical meaning behind the mathematical symbols.
What is the speaker's advice for students studying mathematics?
-The speaker advises students studying mathematics to take great math notes, as it is an absolute requirement for success in the subject.
What kind of resources does the speaker offer for those interested in learning more about math?
-The speaker offers a variety of math courses for middle and high school math, test preparation, and notes for subjects like pre-algebra, algebra, geometry, and trigonometry through his online math help program.
How does the speaker aim to help independent learners and those struggling with math?
-The speaker aims to help independent learners and those struggling with math by providing a comprehensive math program, detailed notes, and one-on-one assistance through his contact form.
Outlines
📚 Introduction to Calculus Notation
This paragraph introduces the basics of calculus notation, aiming to demystify the subject for beginners. The speaker emphasizes that calculus, while powerful and intriguing, often intimidates people due to its unfamiliar symbols. The goal is to make the audience understand that calculus, despite its complexity, is accessible and has significant applications in everyday life, particularly in technology and engineering.
📈 Understanding Calculus Symbols and Functions
The speaker delves into the specific symbols used in calculus, starting with the elongated 'S' which represents summation. He explains that this symbol is used to denote the addition of values, which is a fundamental concept in calculus. The paragraph also introduces the concept of a function in mathematics, using the example of 3x^2, and explains how functions are represented graphically, specifically as parabolas in this case. The x-axis and the concept of boundaries for integration are also briefly discussed.
📊 Exploring Integration and the Calculus Process
Integration, a core concept in calculus, is introduced as the process of adding up values, specifically the area under a curve. The speaker uses the example of finding the area under the curve of the function 3x^2 between the numbers 2 and 5. He explains the process of estimation using rectangles and how making these rectangles infinitely thin (integration) can lead to a precise calculation of the area. The 'dx' notation is mentioned as part of calculus problems, though its detailed explanation is reserved for further study.
🌟 Simplifying Calculus and Encouraging Learning
The speaker concludes by emphasizing that while calculus is a challenging subject, it is learnable even for those not naturally inclined towards math. He encourages viewers to understand the practical significance of calculus symbols and to approach the subject with an open mind. The speaker also promotes his math resources for further learning and concludes with a positive note, wishing viewers well in their mathematical endeavors.
Mindmap
Keywords
💡Calculus
💡Notation
💡Integration
💡Function
💡Graph
💡Elongated S (Integration Symbol)
💡Summation
💡Parabolas
💡Notes
💡Education
💡Technology
Highlights
The video aims to introduce basic calculus notation and demystify the subject for beginners.
Calculus is an intriguing and extremely powerful branch of mathematics with widespread applications.
The video is designed for everyone, regardless of their mathematical background.
Calculus has solved many significant problems and is central to modern technology and engineering.
John, the founder of Taba Class Math, introduces himself as a middle and high school math teacher.
John has created an online math program offering over a hundred courses for middle and high school math.
The concept of integration in calculus involves adding up areas under a function's graph.
The elongated 'S' symbol represents summation and is related to adding things up in calculus.
Functions in mathematics are rules that can be represented graphically.
The 'dx' notation is related to derivatives, another important topic in calculus.
To find the area under a curve in calculus, one must consider infinitely thin rectangles.
John emphasizes the importance of taking good math notes for success in mathematics.
Calculus can be challenging but is accessible with the right approach and background knowledge.
John's YouTube channel offers a range of math videos from basic to advanced levels.
The video encourages viewers to look up calculus symbols to gain a better understanding of the subject.
John's math help program and resources are available for those interested in learning more about mathematics.
Transcripts
Browse More Related Video

Calculus, explained at a very BASIC level…
Algebra vs. Calculus – What’s The Difference?
Let’s Learn a “Little” Calculus - step-by-step…
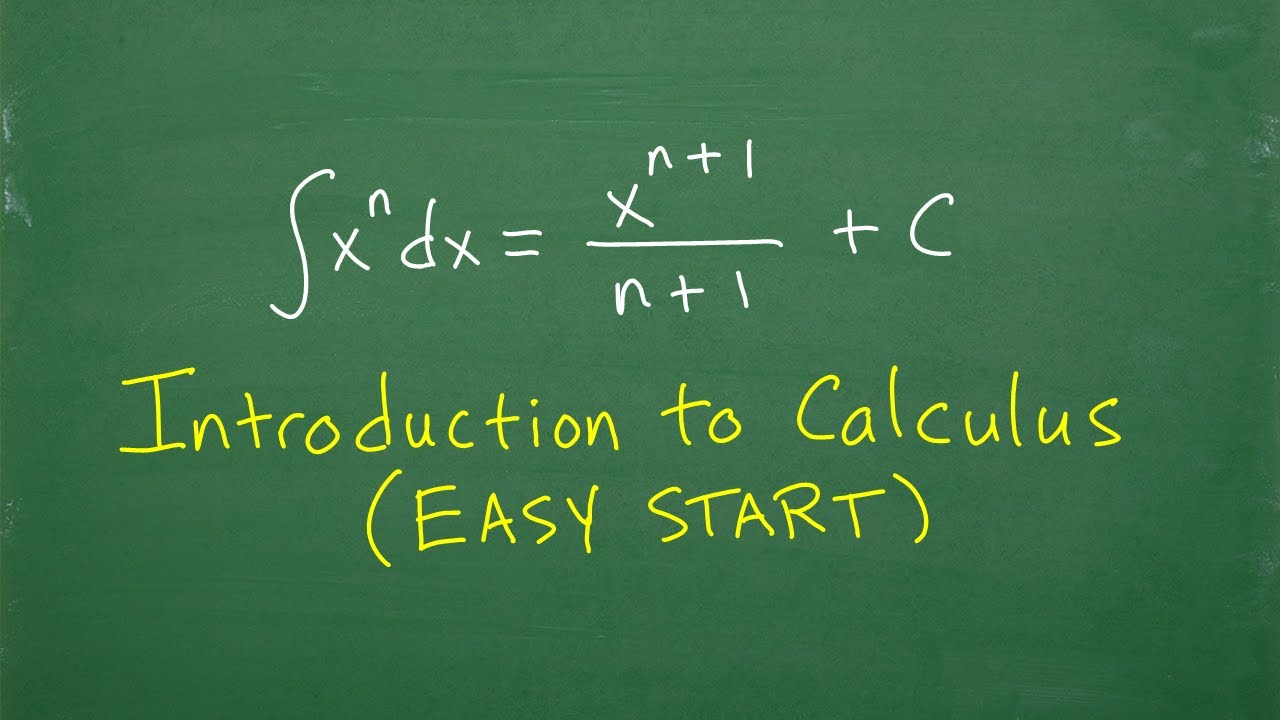
EASY CALCULUS Introduction – Anyone with BASIC Math skills can understand….

Your First Basic CALCULUS Problem Let’s Do It Together….
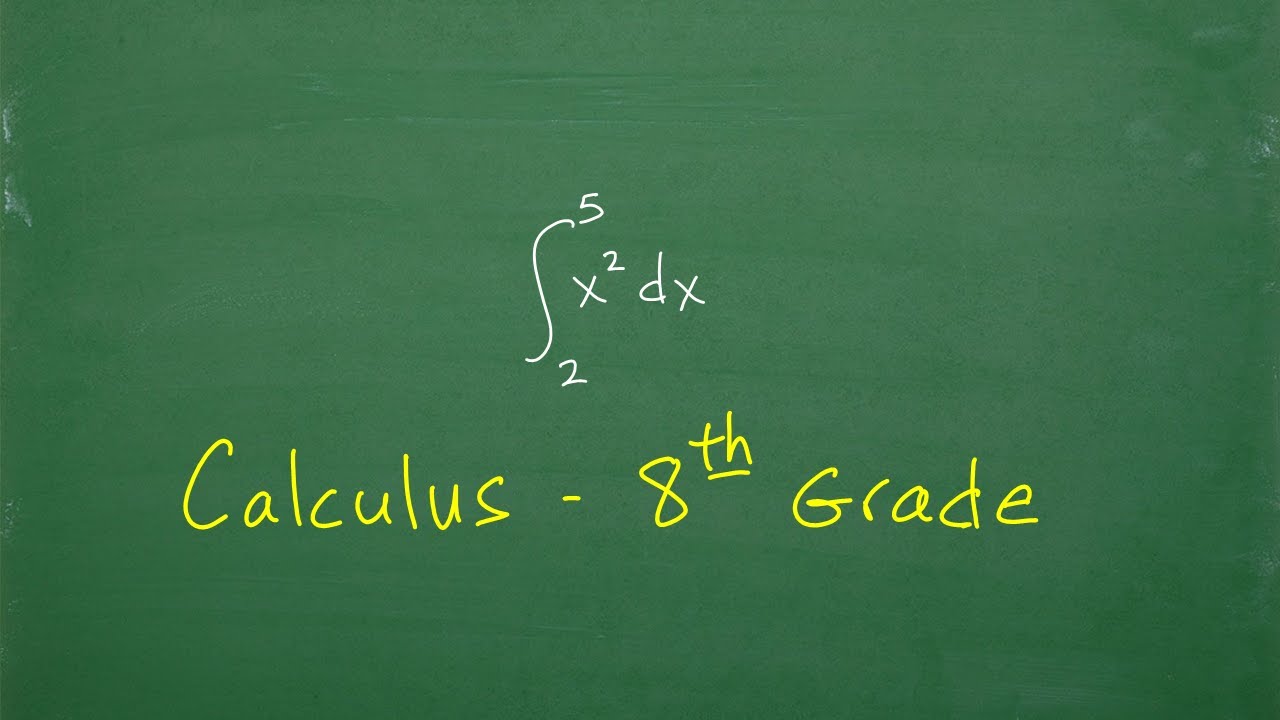
Calculus – taught at the 8th grade level
5.0 / 5 (0 votes)
Thanks for rating: