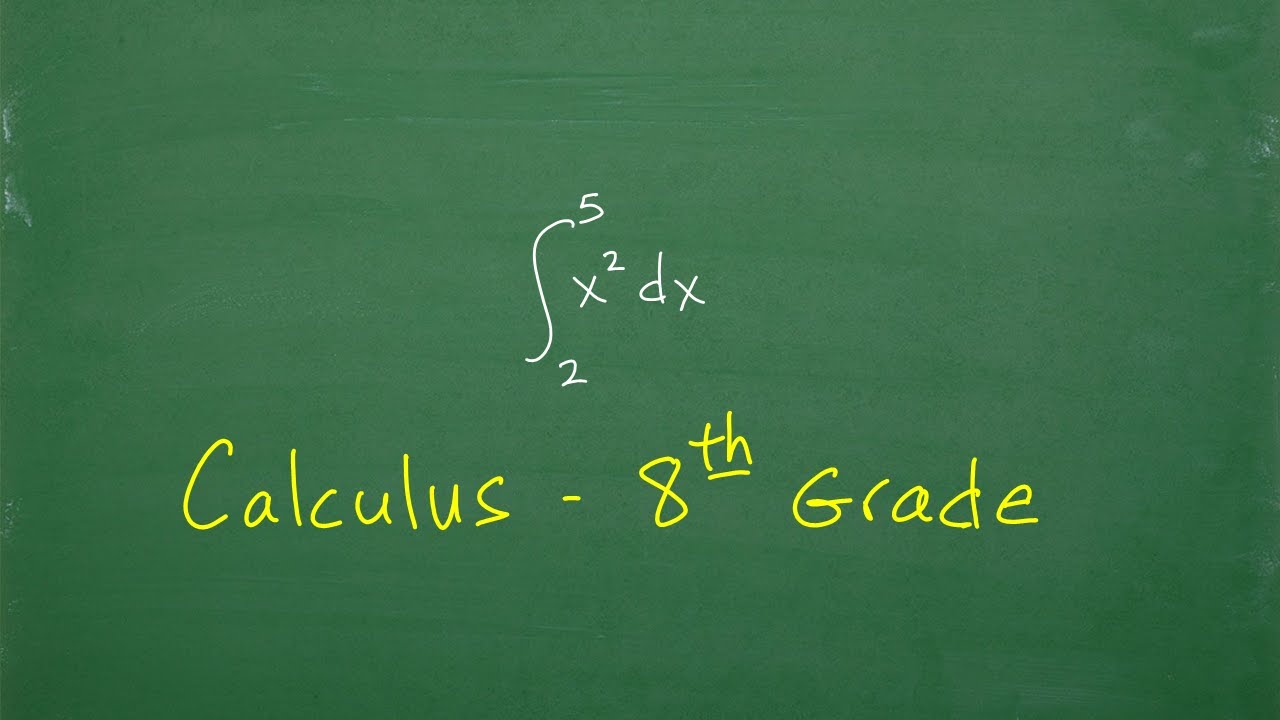How to do Calculus in Under 10 Minutes
TLDRIn this informative video, Josh from Tech Math Channel offers a concise introduction to calculus, focusing on its two primary applications: calculating the area and volume of complex shapes, and determining rates of change. He explains how calculus can handle shapes without a standard formula by using integration, demonstrated through finding the area under a curve. Additionally, he discusses the concept of derivatives to find the exact slope of a curve at any point, showing how calculus provides precise mathematical insights into complex problems.
Takeaways
- 📚 Calculus is a fundamental part of mathematics with applications in understanding complex shapes and rates of change.
- 🌟 Calculus helps in determining the area and volume of complex shapes where traditional geometric formulas may not apply.
- 📊 The video introduces the concept of integration in calculus, which is used to find the area under a curve between two points.
- 🔢 An example is provided where the area under a curve defined by the function f(x) = x^2 between x=3 and x=5 is calculated using integration.
- 📈 The concept of rates of change is discussed, highlighting how calculus can determine the slope or rate of change at any specific point on a curve.
- 🤔 The video addresses the challenge of finding slopes on non-linear graphs, such as stock market graphs, where the slope changes throughout.
- 🧮 The derivative is introduced as a tool in calculus to find the exact slope of a curve at a given point, demonstrated with the function f(x) = 2x^2 - 3x + 2.
- 📚 The process of differentiating the function is shown, transforming it into a derivative to find slopes at various x-values.
- 👍 The video encourages viewers to like, comment, and subscribe if they found the content helpful or learned something new.
- 🙏 A shout out is given to the patrons supporting the Tech Math Channel, with a link provided in the video description for support.
- 👋 The video concludes with a prompt to see the viewers in the next episode, reinforcing the educational and ongoing nature of the channel.
Q & A
What is the primary purpose of calculus in mathematics?
-Calculus is primarily used in mathematics to understand the area and volume of complex shapes, as well as to determine rates of change at any given point.
How does calculus help in determining the area of complex shapes?
-Calculus uses integration to calculate the area of complex shapes where standard geometric formulas may not apply. By integrating the function that describes the curve of the shape over a given interval, one can find the area under the curve.
What is the basic formula to calculate the area of a rectangle?
-The basic formula to calculate the area of a rectangle is length multiplied by width (Area = length * width).
How is the area of a circle calculated?
-The area of a circle is calculated using the formula π * radius^2, where π (pi) is approximately equal to 3.14.
What is an example of a function used in the script to describe a curve?
-An example of a function used in the script to describe a curve is f(x) = x^2, which represents a parabolic curve.
How does calculus find the exact slope of a curve at a specific point?
-Calculus uses the concept of derivatives to find the exact slope of a curve at a specific point. By taking the derivative of the function that describes the curve, one can determine the slope at any given x-value on the curve.
What is the basic rule for integrating a function of the form x^n?
-The basic rule for integrating a function of the form x^n is to increase the power by one and then divide by the new power (integral of x^n is x^(n+1)/(n+1) + C, where C is the constant of integration).
How does the concept of a derivative relate to rates of change?
-The derivative of a function at a specific point represents the rate of change (slope) of the function at that point. It allows us to find the instantaneous rate of change, which is particularly useful for analyzing functions that change continuously and may not have a constant slope.
What does the slope of a linear graph represent?
-The slope of a linear graph represents the rate of change or incline of the line. It is calculated as the rise (change in y) over the run (change in x) between any two points on the line.
What is the significance of calculus in understanding complex graphs like a share market graph?
-Calculus is significant in understanding complex graphs like a share market graph because it allows us to determine the exact slope or rate of change at any given point on the graph, which can fluctuate and is not constant as in the case of a linear graph.
How does the process of finding the area under a curve using calculus differ from traditional geometric formulas?
-The process of finding the area under a curve using calculus involves integrating the function that describes the curve over a specific interval. This method can handle complex shapes for which traditional geometric formulas may not exist or be applicable.
Outlines
📚 Introduction to Calculus
This paragraph introduces the viewer to the concept of calculus, emphasizing its complexity and the challenge of understanding it in a short time frame. The speaker, Josh, clarifies that the goal is not to master calculus but to gain a basic understanding of its functions. He outlines the two primary uses of calculus in mathematics: calculating the area and volume of complex shapes, and determining rates of change, especially in dynamic situations.
📈 Calculating Areas and Volumes
Josh explains the first use of calculus, which is determining the area and volume of complex shapes. He starts with simple shapes like rectangles and circles, using basic formulas for area calculation. He then transitions to more complex shapes without direct formulas, using calculus to find the area under a curve. An example is provided where the area between the curve y=x^2 and the x-axis from x=3 to x=5 is calculated using integration, demonstrating the fundamental rule of calculus for area calculation.
🔄 Rates of Change
The second part of the video focuses on the concept of rates of change. Josh uses a linear graph to illustrate the basic idea of slope, which is the rise over run. He then moves on to more complex graphs, such as a share market graph, where the slope is not constant. Calculus is introduced as a tool to find the exact slope at any given point on a curve. The concept of the derivative is explained, and an example is given where the derivative of the function y=2x^2 - 3x + 2 is calculated to find the slope at different points on the curve.
Mindmap
Keywords
💡Calculus
💡Area
💡Volume
💡Rate of Change
💡Derivative
💡Integration
💡Function
💡Slope
💡Curve
💡Complex Shapes
💡Polynomial
Highlights
Understanding calculus in under 10 minutes is an introduction to the concepts without mastering them.
Calculus is a pivotal part of mathematics that helps in understanding complex shapes and rates of change.
Calculus is used to calculate the area and volume of complex shapes where traditional formulas may not apply.
The area of a rectangle is calculated by multiplying its length by its width.
The area of a circle is calculated using the formula π * radius^2.
Integration in calculus allows us to find the area under a curve, such as the area between x=3 and x=5 for the function f(x) = x^2.
The integral of a function is found by using integration rules, such as adding 1 to the power and dividing by the new power.
Calculus can handle more complex shapes by integrating functions that describe their curves.
Rates of change, such as slopes on graphs, can be understood using calculus for both linear and non-linear functions.
The slope of a linear graph is calculated as the rise over run between two points.
Calculus enables finding the exact slope at a specific point on a curve, rather than an average slope.
Derivatives are used in calculus to determine the slope of a curve at any given point.
The derivative of a function is calculated by applying derivative rules to each term of the function.
By substituting values into the derivative, the slope at any point on the curve can be found.
Calculus is a powerful tool for solving problems involving complex shapes and varying rates of change.
The video provides a simplified overview of calculus, focusing on its applications in geometry and analysis of rates of change.
The importance of calculus in various fields is highlighted, emphasizing its practical applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: