Trigonometry: Unit Circle

New Planet School

6 Jan 201347:35

EducationalLearning

32 Likes 10 Comments

TLDRThis video from New Planet School delves into the concept of the unit circle, a fundamental tool in trigonometry that defines trigonometric functions and establishes connections between them. The unit circle, a circle of radius one centered at the origin, is used to explain how angles and their corresponding trigonometric values (sine, cosine, and tangent) are related. The video also introduces the concepts of radians and degrees, and how they are used to measure angles. By exploring the unit circle and its relationship with right triangles, the video helps viewers understand the trigonometric functions without the need for memorization, using the Pythagorean theorem to generate points on the circle and illustrating the periodic nature of these functions.

Takeaways

📐 The unit circle is a fundamental concept in trigonometry, providing a visual way to understand and define trigonometric functions.
🔍 Understanding the unit circle helps to see the connections between different trigonometric concepts without relying solely on memorization.
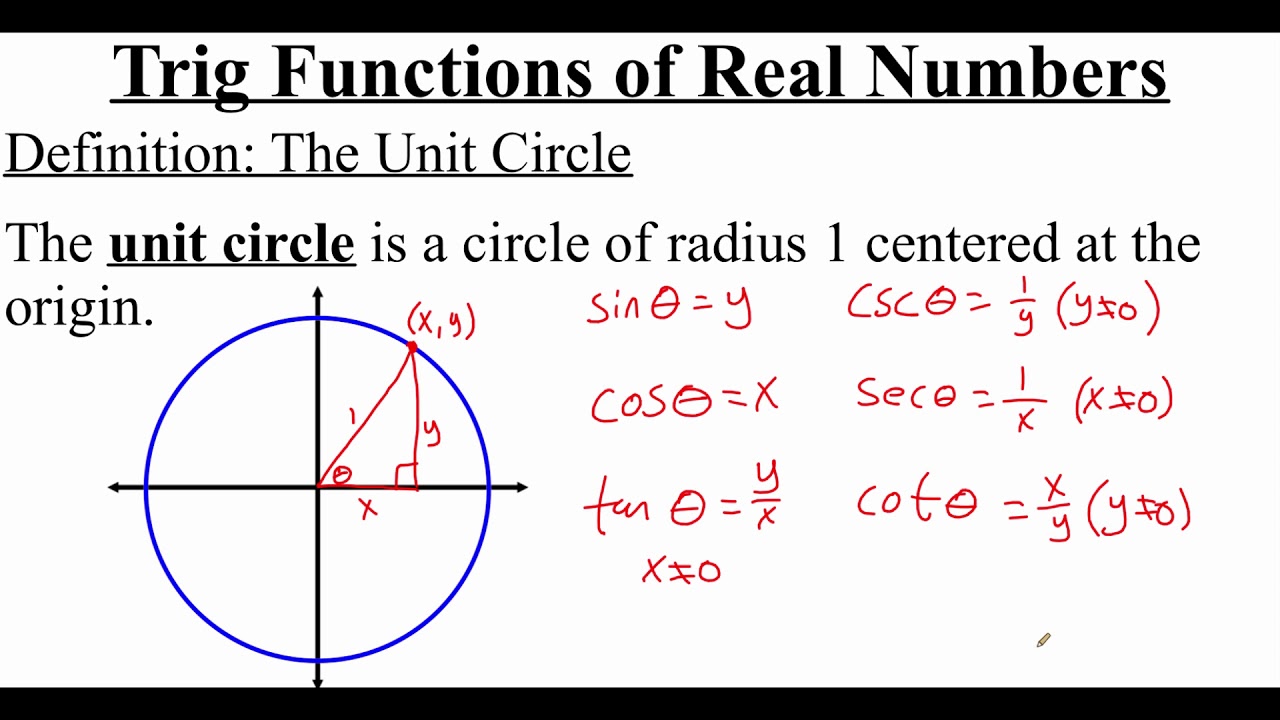
📈 The unit circle is a circle of radius 1 centered at the origin, with points on the circle having coordinates (x, y) that satisfy the equation x^2 + y^2 = 1.
🤔 Trigonometric functions can be visualized and understood through the unit circle, where sine and cosine represent the y-value and x-value of a point on the circle, respectively.
📊 The tangent function is the ratio of sine to cosine, representing the steepness of the tangent line to the unit circle at a given angle.
🌐 The unit circle can be used to graph the basic trigonometric functions, revealing their periodic nature and how they relate to angles.
📐📐 The Pythagorean theorem is directly related to the unit circle, as the theorem's formula (a^2 + b^2 = c^2) describes all points on the unit circle where c equals 1.
🤓 The mnemonic 'sohcahtoa' helps remember the basic relationships: sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent.
🔄 Trigonometric functions are periodic, which is crucial for their applications in fields like math, engineering, physics, and chemistry.
🎓 Further exploration of trigonometry should include a deeper understanding of sine, cosine, and tangent functions, as well as their applications in solving triangles.

Q & A

What is the unit circle and why is it central to trigonometry?
-The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. It is central to trigonometry because it helps define trigonometric functions and establishes connections between different concepts within the field.
How does understanding the unit circle improve trigonometry knowledge?
-Understanding the unit circle allows for a deeper comprehension of trigonometry, as it reveals connections between different concepts without the need for memorization. It also aids in visualizing and graphing basic trigonometric functions like sine, cosine, and tangent.
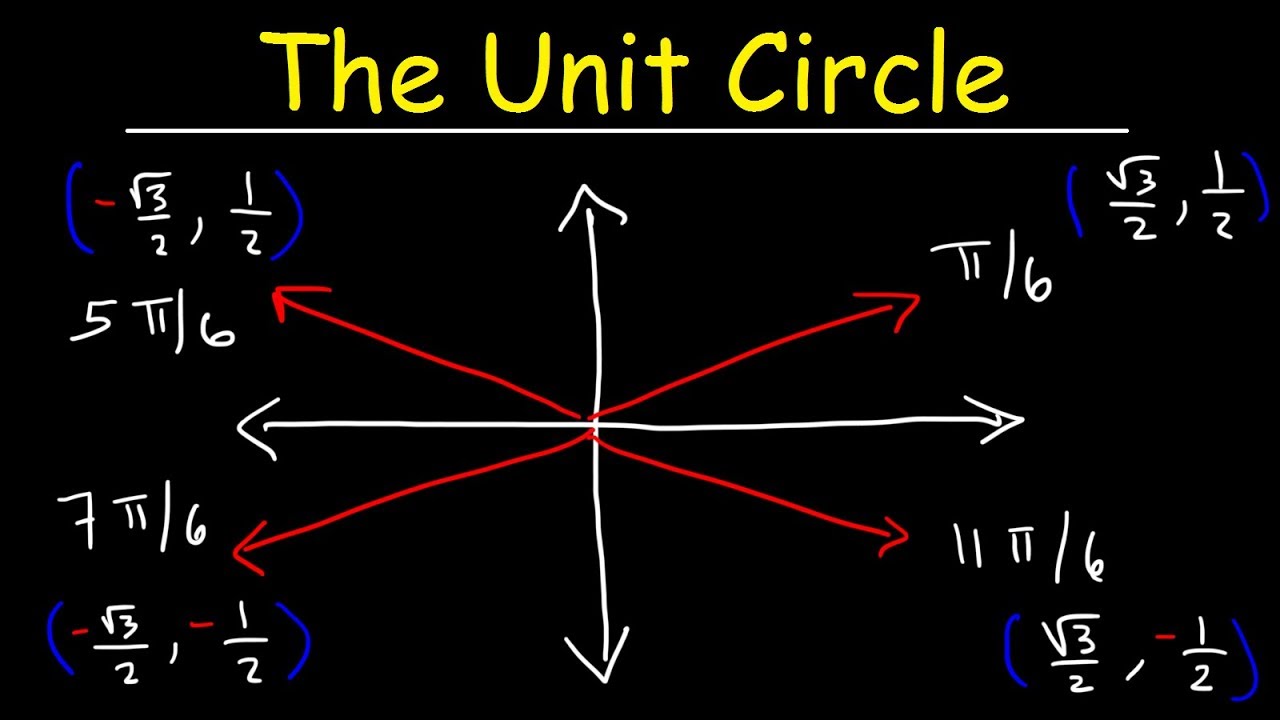
What are the coordinates of the points on the unit circle that correspond to the angles of 0, 45, 90, and 180 degrees?
-At 0 degrees, the coordinates are (1, 0). At 45 degrees, they are (sqrt(2)/2, sqrt(2)/2). At 90 degrees, the coordinates are (0, 1). And at 180 degrees, they are (-1, 0).
How is the unit circle related to the Pythagorean theorem?
-The unit circle is related to the Pythagorean theorem because every point on the unit circle satisfies the equation x^2 + y^2 = 1, which is a specific case of the Pythagorean theorem (a^2 + b^2 = c^2) for a right triangle with hypotenuse of length 1.
What are radians and how do they relate to the unit circle?
-Radians are a measure of angle size in which the angle subtended by an arc of a unit circle is called 1 radian. Radians are used in trigonometry because they provide a direct relationship between angles and the lengths of the arcs on the unit circle.
What is the definition of the sine function in terms of the unit circle?
-The sine function is defined as the y-coordinate of a point on the unit circle, which corresponds to the opposite side of the right triangle formed by the radius and the line segment from the origin to the point on the circle.
How can you use the unit circle to graph the sine and cosine functions?
-By plotting points on the unit circle at various angles and determining their x (cosine) and y (sine) coordinates, you can create the graphs of the sine and cosine functions. These graphs will show the periodic nature of these trigonometric functions.
What is the tangent function and how is it related to sine and cosine?
-The tangent function is defined as the ratio of the sine function to the cosine function, or equivalently, as the y-coordinate divided by the x-coordinate of a point on the unit circle.
What mnemonic can be used to remember the relationships between sine, cosine, and tangent with respect to a right triangle?
-The mnemonic 'sohcahtoa' can be used to remember that sine is the opposite side over the hypotenuse, cosine is the adjacent side over the hypotenuse, and tangent is the opposite side over the adjacent side.
How does the unit circle demonstrate the periodic nature of trigonometric functions?
-The unit circle demonstrates the periodic nature of trigonometric functions by showing that as you move around the circle, the sine and cosine values repeat in a cycle. For example, after completing a full circle (360 degrees or 2π radians), the values return to their starting points.
Why is it important to understand both degrees and radians when studying trigonometry?
-Understanding both degrees and radians is important because they are both ways of measuring angles. While degrees are commonly used in everyday life, radians are particularly useful in trigonometry and calculus. Being able to convert between these two systems is crucial for accurate calculations and problem-solving in these fields.

Outlines

00:00

📚 Introduction to Trigonometry and the Unit Circle

This paragraph introduces the concept of the unit circle, a fundamental aspect of trigonometry. It emphasizes the importance of understanding the unit circle to grasp the connections between different trigonometric functions and relationships. The speaker suggests that by comprehending the unit circle, one can visualize the trigonometric functions sine, cosine, and tangent, and their interconnections without the need for memorization.

05:02

📐 Understanding the Unit Circle and Angles

The paragraph delves into the specifics of the unit circle, describing it as a circle with a radius of 1 and how points on the circle can be defined by their x and y coordinates. It introduces the general formula for a circle centered at the origin and explains how the unit circle fits this formula. The paragraph also discusses the measurement of angles in degrees and radians, highlighting the significance of radians in trigonometry and providing an example to illustrate their relationship to the unit circle.

10:02

📌 Defining Trigonometric Functions using the Unit Circle

This section explains how trigonometric functions can be defined using the unit circle. It describes the sine function as the y-value of a point on the unit circle and the cosine function as the x-value. The paragraph uses the concept of a right triangle inscribed in the unit circle to relate the angle to the coordinates of the point. It also introduces the tangent function as the ratio of sine to cosine and provides a mnemonic, 'sohcahtoa', to remember the relationships between the trigonometric functions and the sides of a right triangle.

15:04

🔄 Trigonometric Functions and the Unit Circle

The paragraph further explores the trigonometric functions, emphasizing their periodic nature and how they can be visualized on the unit circle. It explains how the sine and cosine functions can be graphed by moving around the unit circle and provides a method for generating the points on the circle. The speaker also connects the unit circle to the Pythagorean theorem, showing how it can be used to generate points on the circle and understand the relationships between angles and their corresponding trigonometric values.

20:05

🌐 Applications and Further Study of Trigonometric Functions

In this concluding paragraph, the speaker discusses the applications of trigonometric functions in various fields such as math, engineering, physics, and chemistry. It highlights the periodic nature of sine and cosine functions and their relevance in understanding periodic phenomena like light and sound waves. The speaker encourages further study by suggesting additional resources and exercises, such as watching other educational videos and practicing with blank unit circles to solidify understanding.

Mindmap

Keywords

💡Unit Circle

The unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane. It is a fundamental concept in trigonometry, as it helps define trigonometric functions and their relationships with angles. In the video, the unit circle is used to explain how sine, cosine, and tangent functions can be visualized and understood in relation to angles and their corresponding points on the circle.

💡Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. It is widely used in various fields such as physics, engineering, and astronomy to model periodic phenomena. The video focuses on trigonometric functions and their connection to the unit circle.

💡Sine Function

The sine function, often abbreviated as sin, is one of the primary trigonometric functions. It relates the angle of a right triangle to the ratio of the length of the opposite side to the length of the hypotenuse. In the context of the unit circle, the sine of an angle corresponds to the y-coordinate of a point on the circle.

💡Cosine Function

The cosine function, abbreviated as cos, is another key trigonometric function. It is the ratio of the adjacent side to the hypotenuse in a right-angled triangle. For the unit circle, the cosine of an angle is the x-coordinate of a point on the circle, representing the horizontal position relative to the origin.

💡Tangent Function

The tangent function, denoted as tan, is the ratio of the opposite side to the adjacent side in a right-angled triangle. In terms of the unit circle, the tangent of an angle is the y-coordinate divided by the x-coordinate of a point on the circle, representing the steepness or slope of the line from the origin to that point.

💡Radians

Radians are a unit of measure for angles, which are used extensively in trigonometry and calculus. One radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. The video explains that radians provide a way to measure angles that is directly related to the length of the arc on the unit circle.

💡Periodic Functions

Periodic functions are mathematical functions that repeat their values in regular intervals. The sine and cosine functions are classic examples of periodic functions, with a period of 2π in the context of the unit circle. This means that the function values repeat every 2π radians or angles.

💡Pythagorean Theorem

The Pythagorean theorem is a fundamental principle in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem is used in the video to relate the unit circle to right triangles and to generate points on the circle.

💡Mnemonic

A mnemonic is a device, method, or pattern that helps to improve memory retention. In the context of the video, the mnemonic 'sohcahtoa' is introduced to help remember the basic relationships of trigonometric functions to the sides of a right triangle: sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent.

💡Graphing Trigonometric Functions

Graphing trigonometric functions involves visually representing the mathematical behavior of sine, cosine, and tangent functions on a coordinate plane. The video explains how understanding the unit circle can help in plotting these functions and visualizing their periodic nature and overall shape.

Highlights

The unit circle is a central concept in trigonometry that helps define trigonometric functions and make connections within the field.

Understanding the unit circle can reduce the need for memorization and help visualize the relationships between different trigonometric concepts.

The unit circle is a circle with a radius of 1, and all points on it have a length from the origin to any point on the circle equal to 1.

The general formula for a circle centered at the origin is x^2 + y^2 = radius^2, and for the unit circle, this simplifies to x^2 + y^2 = 1.

Angles in trigonometry can be measured in degrees and radians, with radians being a new concept that measures the length of the arc of the unit circle.

One full rotation around the unit circle in radians is 2π, which is equivalent to 360 degrees.

Trigonometric functions such as sine, cosine, and tangent can be defined using the unit circle and right triangles.

The sine function is defined as the y-value (opposite side) of a right triangle on the unit circle, and cosine as the x-value (adjacent side).

The tangent function is the ratio of sine to cosine, or the y-value over the x-value on the unit circle.

The unit circle provides a visual tool to understand and remember trigonometric relationships and the graphs of sine, cosine, and tangent functions.

The mnemonic 'sohcahtoa' can be used to remember the relationships: sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent.

The Pythagorean theorem is directly related to the unit circle, as the theorem applies to the right triangles formed within the circle.

By understanding the unit circle and the Pythagorean theorem, one can generate points on the circle and understand the periodic nature of trigonometric functions.

Trigonometric functions are periodic and have practical applications in various fields such as math, engineering, physics, and chemistry.

The unit circle can be used to graph the sine and cosine functions, which are wave-like and repeat their patterns.

The tangent function has a unique graph shape due to the ratio of sine to cosine, which includes asymptotes where cosine is zero.

By drawing the unit circle and understanding the trigonometric functions, one can visualize and calculate values for any angle within the circle.

Transcripts

Browse More Related Video

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles

4.3.4 Trigonometric Functions of Real Numbers

Trig 0.2 - Trig Functions Defined on the Unit Circle

An Indepth Look at Using Inverse Trig Functions (Precalculus - Trigonometry 21)

The Unit Circle, Basic Introduction, Trigonometry

Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)

Related Tags

Trigonometry Unit Circle Sine Function Cosine Function Tangent Function Math Education Pythagorean Theorem Periodic Functions New Planet School Trigonometric Relationships