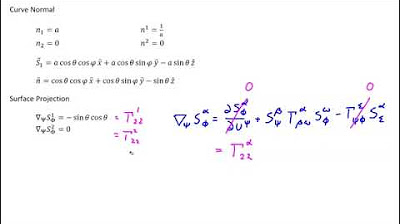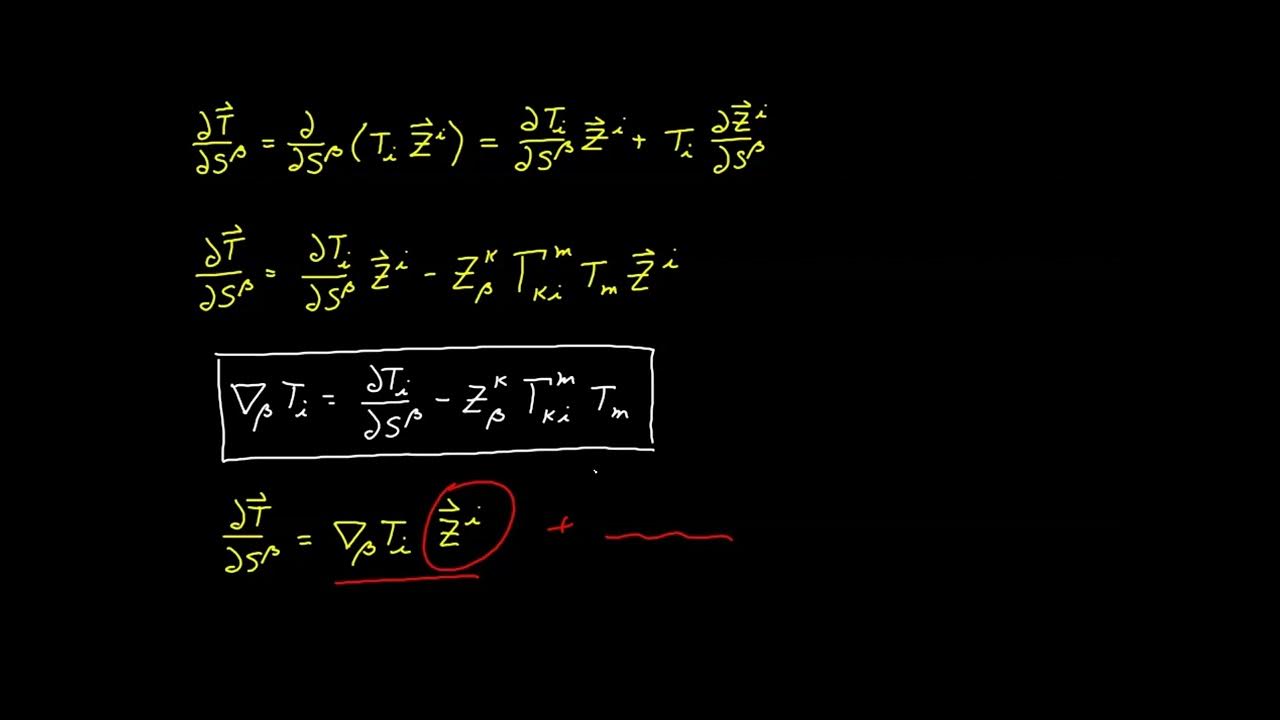Video 74 - Weingarten's Formula
TLDRIn this 74th installment of the tensor calculus series, the video explores the surface covariant derivative, deriving relationships involving the shift tensor and normal vector. The script delves into the non-metronic nature of the surface basis vector and its implications for the shift tensor and curvature tensor. It introduces Weingarten's formula, providing a method to evaluate the surface covariant derivative of the normal using the curvature tensor. The video concludes by comparing the complexity of different expressions for evaluating the curvature tensor, highlighting the efficiency of using affine coordinates in tensor operations.
Takeaways
- 📚 The video discusses tensor calculus, specifically focusing on the surface covariant derivative and its relationships with the shift tensor and curvature tensor.
- 🔍 The surface basis vector is not metronomic with respect to the surface covariant derivative, leading to a non-zero value that is explored in the video.
- 🔄 A substitution is made for the surface basis vector using the shift tensor, which is a key step in deriving the relationships between tensors.
- 📉 The video derives an expression for the surface covariant derivative of the shift tensor and relates it to the curvature tensor.
- 📈 Weingarten's formula is introduced, which provides a way to calculate the surface covariant derivative of the normal vector as a function of the curvature tensor.
- 🔗 The relationship between the shift tensor and curvature tensor is established in two forms, allowing for the evaluation of one in terms of the other.
- 📝 The curvature tensor can be derived from the surface covariant derivative of the shift tensor or vice versa, offering two methods for its evaluation.
- 🧩 The video also explores the orthogonality of the surface covariant basis vectors to the normal, leading to an alternate expression for the curvature tensor.
- 🔄 The indexes are manipulated to invert expressions and isolate terms, providing different perspectives on the relationship between tensors.
- 📐 The use of affine coordinates simplifies the evaluation of the curvature tensor, reducing the number of terms that need to be considered.
- 🔑 The final takeaway is the preference for using the simplified expression for the curvature tensor when working with affine coordinates, as it significantly reduces computational complexity.
Q & A
What is the main focus of this video in the series on tensor calculus?
-The main focus of this video is to derive relationships involving the surface covariant derivative, specifically an expression for the surface covariant derivative of the shift tensor and Weingarten's formula, which gives the surface covariant derivative of the normal.
What property of the surface basis vector does the video discuss in relation to the surface covariant derivative?
-The video discusses that the surface basis vector is not metronomic with respect to the surface covariant derivative, meaning the operation does not yield a value of zero.
How is the surface basis vector represented in terms of the shift tensor in the video?
-The surface basis vector s_alpha is represented as the product of z_i (a basis vector) and the shift tensor component z_i^alpha.
What is the significance of the ambient basis vector being metronomic in the context of the video?
-The ambient basis vector being metronomic allows it to be factored out of expressions, simplifying the derivation of relationships between the shift tensor and the curvature tensor.
What is Weingarten's formula and what does it provide?
-Weingarten's formula is an expression that provides the value of the surface covariant derivative of the normal as a function of the curvature tensor.
How does the video derive the relationship between the shift tensor and the curvature tensor?
-The video derives the relationship by starting with the surface basis vector expressed in terms of the shift tensor, using the metronomic property of the ambient basis vector, and then isolating the curvature tensor on one side of the equation.
What does the video suggest about the choice between two expressions for evaluating the curvature tensor?
-The video suggests that the expression involving the surface covariant derivative of the normal is more convenient to use, especially with affine coordinates, as it simplifies to evaluating a single contraction of an ambient index.
What is the role of the normal vector in the derivations presented in the video?
-The normal vector plays a crucial role in the derivations as it is used to decompose and represent the normal in terms of the basis vectors, which is essential in establishing the relationships between the shift tensor, the curvature tensor, and the surface covariant derivative.
How does the video handle the complexity of the expressions when expanding them out?
-The video simplifies the complexity by noting that with affine coordinates, many terms involving the ambient Christoffel symbols drop out, reducing the number of terms that need to be evaluated.
What is the final result derived in the video, and what is its significance?
-The final result derived is Weingarten's formula, which is significant as it provides a way to evaluate the surface covariant derivative of the normal in terms of the curvature tensor, offering a deeper understanding of the geometric properties of surfaces in tensor calculus.
Outlines
📚 Introduction to Surface Covariant Derivatives in Tensor Calculus
This paragraph introduces the topic of the video, which is to derive relationships involving the surface covariant derivative. It focuses on two main relationships: one for the surface covariant derivative of the shift tensor and another known as Weingarten's formula, which relates to the surface covariant derivative of the normal. The paragraph sets the stage by mentioning that the surface basis vector is not metronomic with respect to the surface covariant derivative, leading to a non-zero value. The aim is to use this relationship to develop further connections between the shift tensor and the curvature tensor.
🔍 Deriving Relationships Between Shift Tensor and Curvature Tensor
The second paragraph delves into the derivation of a relationship between the surface covariant derivative of the shift tensor and the curvature tensor. It starts by substituting the surface basis vector with the shift tensor and then uses the metronomic property of the ambient basis vector to isolate terms. The paragraph explains how to factor out common terms and invert the relationship to isolate the curvature tensor. This leads to two expressions that can be used to evaluate either the surface covariant derivative of the shift tensor or the curvature tensor itself, depending on the known quantities.
📘 Exploring Weingarten's Formula and Curvature Tensor
This paragraph continues the exploration by focusing on Weingarten's formula, which provides an expression for the surface covariant derivative of the normal in terms of the curvature tensor. It begins with an expression from a previous video that establishes the orthogonality of the surface covariant basis vectors to the normal. The paragraph then takes the surface covariant derivative of this expression, applies the product rule, and simplifies the result using the previously derived curvature tensor relationship. The goal is to isolate terms to evaluate the curvature tensor in a different manner than before.
🔄 Manipulating Indices to Isolate Curvature Tensor Expressions
The fourth paragraph discusses the manipulation of indices to derive an alternate form for evaluating the curvature tensor. It involves raising and lowering indices and flipping the positions of certain indices to simplify the expression. The paragraph introduces the concept of the surface projection operator and its relationship to the identity derived in a previous video. The aim is to express the curvature tensor in a form that can be evaluated more conveniently, taking into account the properties of the ambient metric tensors.
📝 Conclusion and Weingarten's Formula Finalization
In the concluding paragraph, the video summarizes the achievements of the session, which include deriving relationships between the surface covariant derivatives of both the shift tensor and the normal with the curvature tensor. Two forms of each relationship are presented, one isolating the covariant derivative and the other the curvature tensor. The paragraph also discusses the practicality of using these forms, especially when dealing with affine coordinates, which simplifies the expressions significantly. The final expression, known as Weingarten's formula, is highlighted as a valuable tool for evaluating the surface covariant derivative of the normal.
🚀 Upcoming: Further Exploration of Weingarten's Formula
The final paragraph teases the continuation of the topic in the next video, where the focus will be on further exploration and application of Weingarten's formula. It implies that the upcoming session will delve deeper into the practical evaluation of the formula, likely with specific examples or additional context to aid understanding.
Mindmap
Keywords
💡Tensor Calculus
💡Surface Covariant Derivative
💡Shift Tensor
💡Curvature Tensor
💡Weingarten's Formula
💡Normal Vector
💡Metronomic
💡Ambient Basis Vector
💡Covariant Component
💡Surface Projection Operator
💡Affine Coordinates
Highlights
The video derives relationships involving the surface covariant derivative, focusing on the shift tensor and normal vector.
Introduction to the non-metronic nature of the surface basis vector with respect to the surface covariant derivative.
Development of a relationship between the shift tensor and the curvature tensor using the surface basis vector substitution.
Factoring out the ambient basis vector to isolate terms in the expression for the surface covariant derivative of the shift tensor.
Decomposition of the normal vector using the same basis vector and common factor extraction leading to a new relationship.
Inversion of the derived relationship to isolate the curvature tensor on one side of the equation.
Multiplication by the covariant component of the normal to simplify the expression involving the curvature tensor.
Introduction of Weingarten's formula, which gives the surface covariant derivative of the normal.
Derivation of an alternate form for evaluating the curvature tensor based on the derivative of the normal.
Exploration of the orthogonality of the surface covariant basis vectors to the normal using an expression from a previous video.
Use of the product rule in taking the surface covariant derivative of the expression involving the normal vector.
Substitution of the curvature tensor into the derived expression to simplify and find a relationship.
Manipulation of indices to isolate different terms in the expression for the curvature tensor.
Introduction of the surface projection operator and its relationship with the normal and surface projection operators.
Derivation of Weingarten's formula by distributing terms and using the properties of the unit normal vector.
Final expression of Weingarten's formula, relating the surface covariant derivative of the normal to the curvature tensor.
Recap of the video's content, summarizing the derived relationships and their potential applications.
Discussion on the practicality of using different forms of the derived relationships in affine coordinates.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: