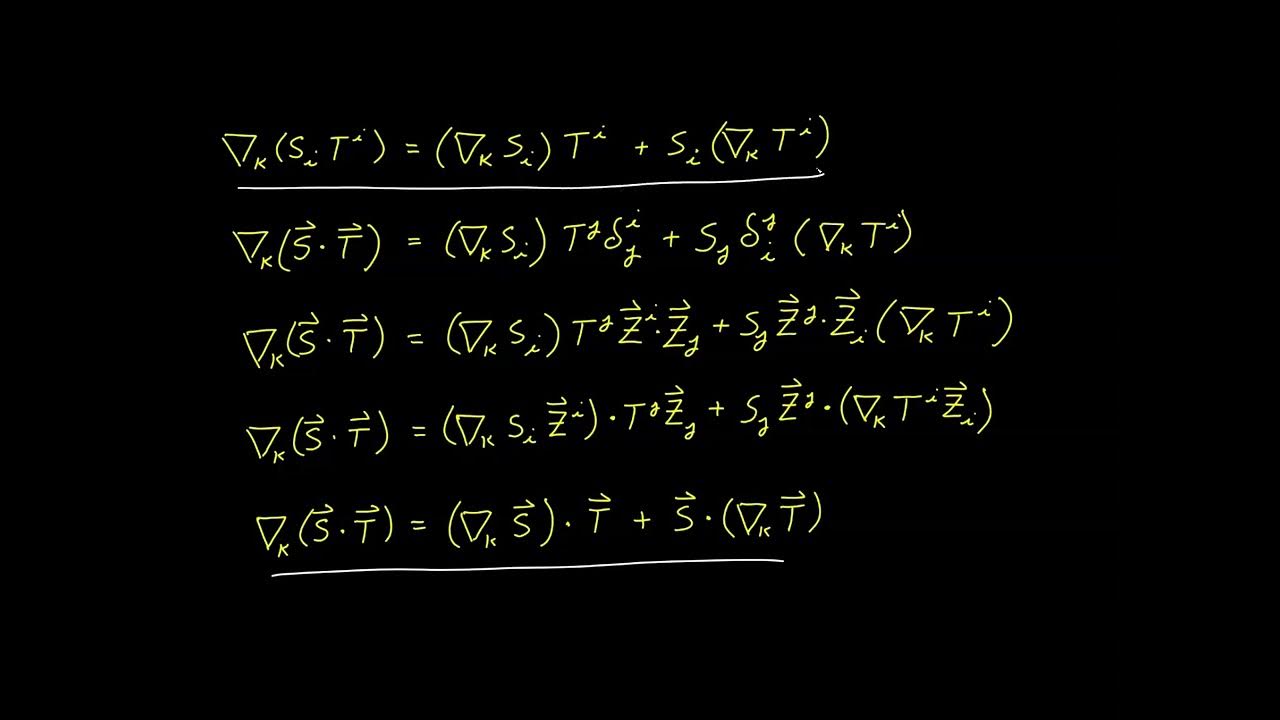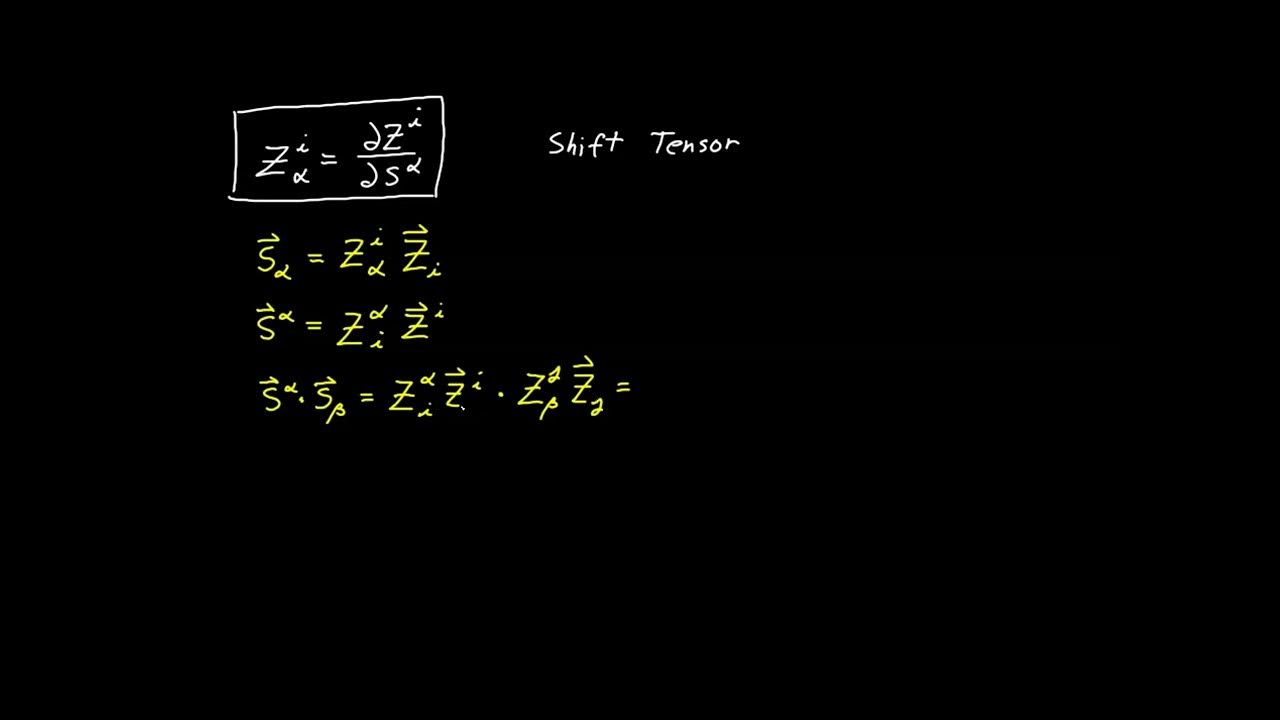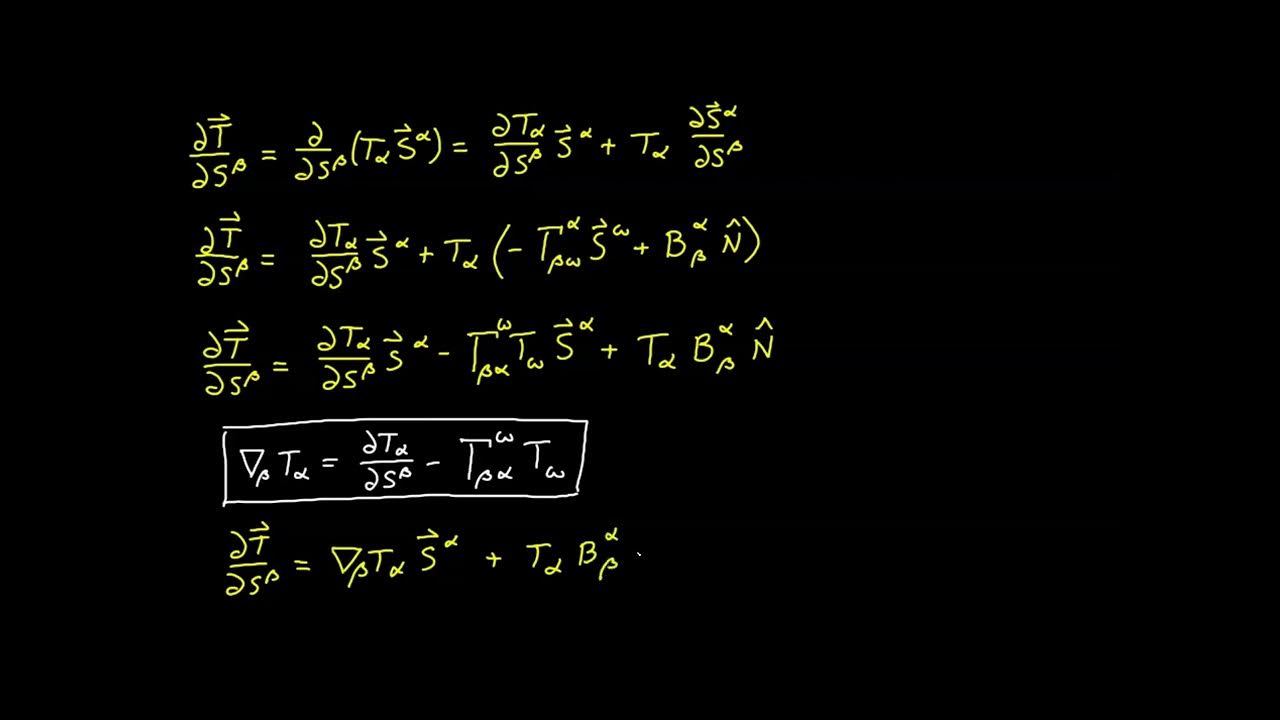Video 72 - Surface Covariant Derivative for Non Tangent Vectors
TLDRIn this video on tensor calculus, the focus shifts to analyzing the surface covariant derivative for vectors outside the tangent plane, using ambient coordinates. The presenter introduces two new forms of the surface covariant derivative for contravariant and covariant vector components with ambient indices. The video also explores the chain rule, illustrating how the surface covariant derivative relates to the normal covariant derivative through the shift tensor, and highlights the preservation of the metronomic property for tensors with ambient indices. The summary concludes with the application of these concepts to higher-rank tensors.
Takeaways
- 📚 The video discusses the extension of the analysis of the surface covariant derivative to tensors not in the tangent plane, using ambient coordinates to represent any vector in the ambient space.
- 🔍 The product rule is applied to analyze the covariant derivative, with the chain rule used to expand the partial derivative of basis vectors.
- 📐 The shift tensor, introduced in a previous video, plays a crucial role in the analysis of vectors outside the tangent plane, being part of the new expressions derived.
- 🔄 The script explains the process of deriving two new forms of the surface covariant derivative for contravariant and covariant vector components with ambient indices.
- 📝 The surface covariant derivative is defined in a new way for vectors with ambient indices, involving the shift tensor and the Christoffel symbols.
- 🔗 The new forms are similar to the standard covariant derivative, with the inclusion of the shift tensor being the main difference.
- 📚 The script illustrates the application of the new forms to higher-rank tensors, showing that the pattern of derivation is consistent with previous videos.
- 🔑 A unique property of the surface covariant derivative is introduced, the chain rule, which relates it to the normal covariant derivative by the addition of the shift tensor.
- 📉 The metronomic property, which results in zero when applied to certain tensors like the metric tensor, is preserved for the surface covariant derivative when applied to tensors with ambient indices.
- 🔍 The chain rule is applicable to tensors of higher rank as well, showing that the surface covariant derivative equals the normal covariant derivative times the shift tensor for tensors with exclusively ambient indices.
- 🔚 The video concludes with a recap of the new forms derived and their properties, emphasizing their similarity to the standard covariant derivative and the applicability of the chain rule.
Q & A
What is the focus of Video 72 in the Tensor Calculus series?
-Video 72 focuses on extending the analysis of the surface covariant derivative to tensors that do not lie in the tangent plane.
Why is the linear combination used in the last video not applicable to vectors outside the tangent plane?
-The linear combination used in the last video is not applicable because it only works for vectors that lie within the tangent plane. For vectors outside the tangent plane, a different approach using ambient coordinates is necessary.
How are vectors that lie outside the tangent plane represented in the analysis?
-Vectors that lie outside the tangent plane are represented using ambient coordinates, specifically using a linear combination involving the ambient coordinates t_i and z_i.
What role does the chain rule play in this analysis?
-The chain rule is used to expand certain terms, particularly when expressing ambient basis vectors as functions of surface coordinates. This allows for the correct application of derivatives in the analysis.
What is the significance of the shift tensor in this context?
-The shift tensor, denoted as z_k^beta, is significant because it helps express the relationship between partial derivatives of ambient coordinates and surface coordinates, which is crucial for analyzing vectors with ambient indexes.
How does the surface covariant derivative differ when applied to vectors with ambient indexes compared to those with surface indexes?
-When applied to vectors with ambient indexes, the surface covariant derivative includes the shift tensor in its definition. This is different from the standard covariant derivative, which applies to vectors with surface indexes and does not include this additional factor.
What is the 'chain rule' property in the context of surface covariant derivatives?
-The 'chain rule' property states that the surface covariant derivative of a vector with ambient indexes can be expressed as the normal covariant derivative multiplied by the shift tensor. This property is exclusive to tensors with ambient indexes.
Why is there no additional term in the surface covariant derivative when using ambient basis vectors?
-There is no additional term because the ambient basis vectors are sufficient to represent a vector pointing in any direction within the ambient space, unlike in the surface case where an additional term might be needed to account for the normal direction.
What does the video illustrate about applying the surface covariant derivative to tensors of higher rank?
-The video illustrates that when applying the surface covariant derivative to higher-rank tensors, the process follows a similar pattern to the standard covariant derivative, but it includes the shift tensor due to the ambient indexes.
What is the overall significance of the results derived in this video?
-The results show that surface covariant derivatives for vectors with ambient indexes closely resemble the standard covariant derivatives but require adjustments like the inclusion of the shift tensor. These results maintain consistency across various tensor ranks and provide a useful tool for analyzing non-tangent vectors in the ambient space.
Outlines
📚 Introduction to Non-Tangent Vector Analysis in Tensor Calculus
This paragraph introduces the extension of tensor calculus analysis to non-tangent vectors, which lie outside the tangent plane of a surface. It explains that the previous analysis was limited to vectors within the tangent plane and that a linear combination was used for that analysis. The new approach involves using ambient coordinates to represent any vector in the ambient space, starting with the product rule and expanding the analysis using the chain rule for partial derivatives. The paragraph also discusses the shift tensor and the Christoffel symbols in the context of the surface covariant derivative.
🔍 Deriving New Forms of Surface Covariant Derivative for Ambient Index Vectors
The second paragraph delves into the derivation of new forms for the surface covariant derivative, specifically for vectors with an ambient index in the upper position. It highlights the similarity and differences with the basic covariant derivative and the necessity of including the shift tensor in the new definition. The paragraph also explains how the ambient basis can represent vectors in any direction, eliminating the need for additional terms. It concludes with the fourth form of the surface covariant derivative for a covariant vector component with an ambient index in the lower position.
🔗 Chain Rule and Properties of Surface Covariant Derivative
This paragraph discusses the properties of the newly derived surface covariant derivatives, emphasizing their similarity to the standard covariant derivative and the carryover of properties. It illustrates the application of these derivatives to higher-rank tensors using the same pattern developed in previous videos. The paragraph also introduces a property unique to the surface covariant derivative when dealing with tensors that have ambient indexes, showing how the surface covariant derivative is related to the normal covariant derivative by the addition of the shift tensor.
📘 Metronymic Property and Chain Rule Application for Higher-Rank Tensors
The fourth paragraph further explores the metronymic property, which states that certain tensors, when acted upon by the covariant derivative, yield zero. It shows that this property holds true for the surface covariant derivative as well, provided the tensors are expressed with ambient indexes. The paragraph demonstrates the application of the chain rule to higher-rank tensors, showing that the surface covariant derivative equals the normal covariant derivative multiplied by the shift tensor, a rule applicable to tensors exclusively with ambient indexes.
🔚 Recap and Preview of Upcoming Analysis on Surface Covariant Derivative Properties
In the final paragraph, the video script provides a recap of the newly derived forms for the surface covariant derivative of non-tangent vectors and their similarities to the standard covariant derivative. It also highlights the chain rule property and its implications for tensors with ambient indexes. The paragraph concludes with a preview of the next video, which will offer a more comprehensive analysis of the surface covariant derivative's properties, including the forms discussed in this and the previous video.
Mindmap
Keywords
💡Surface Covariant Derivative
💡Tangent Plane
💡Ambient Coordinates
💡Product Rule
💡Chain Rule
💡Shift Tensor
💡Christoffel Symbol
💡Metronomic Property
💡Contravariant Vector Component
💡Covariant Vector Component
Highlights
Introduction of extending the analysis of the surface covariant derivative to tensors not in the tangent plane.
Use of ambient coordinates to represent vectors outside the tangent plane.
Explanation of the product rule in the context of surface covariant derivatives.
Application of the chain rule to expand the partial derivative of basis vectors.
Identification of the shift tensor in the expansion of the partial derivative.
Connection between the partial derivative of basis vectors and the Christoffel symbol.
Reordering and renaming indices to simplify the expression for the surface covariant derivative.
Substitution of terms to define the surface covariant derivative for contravariant vector components with ambient indices.
Introduction of a new operator for the surface covariant derivative in the expression.
Derivation of two forms for the surface covariant derivative, one for contravariant and one for covariant vector components.
Comparison of the new forms with the basic covariant derivative from previous videos.
Inclusion of the shift tensor in the surface covariant derivative when dealing with ambient indexes.
Demonstration of how the ambient basis can represent vectors in any direction without additional terms.
Development of a fourth form for the surface covariant derivative of a covariant vector component with an ambient index.
Consistency of the new form with the normal covariant derivative, with minor modifications.
Application of the surface covariant derivative to higher-rank tensors, following a similar pattern to previous videos.
Introduction of the chain rule property for the surface covariant derivative with respect to tensors with ambient indexes.
Illustration of the metronomic property being maintained for the surface covariant derivative of certain tensors.
Recap of the video's content, emphasizing the derivation of new forms and the chain rule property.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: