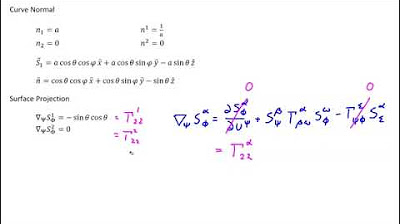Video 75 - Sample Curvature Tensors
TLDRThis video tutorial delves into the evaluation of curvature tensors for various sample surfaces using tensor calculus. The presenter guides viewers through the process of calculating the curvature tensor for a cylindrical, spherical, and torus surface by deriving partial derivatives of the normal vector with respect to surface coordinates. The method involves using the shift tensor, normal vector, and performing matrix contractions to obtain the final tensor results, providing a clear understanding of the curvature properties of these surfaces.
Takeaways
- 📚 The video is part of a series on tensor calculus, specifically focusing on evaluating the curvature tensor for sample surfaces.
- 🔍 A formula derived in a previous video is used to evaluate the curvature tensor, which is composed of a shift tensor and partial derivatives of the normal vector with respect to surface coordinates.
- 📐 The process begins with a cylindrical surface, where the shift tensor and normal vector are provided, and partial derivatives are calculated with respect to theta and z.
- 🌀 For the cylindrical surface, partial derivatives with respect to z are zero, as the components do not depend on z.
- 🧩 The calculation involves a contraction of matrices to form a 2x2 matrix, resulting from the multiplication of a 2x3 and a 3x2 matrix.
- 🔢 The curvature tensor for the cylindrical surface is found to be a 2x2 matrix with specific elements, including negative 'a' and zeros.
- 🌐 Moving on to the spherical surface, the shift tensor and normal vector are given, and the partial derivatives are calculated with respect to theta and phi.
- 📈 The curvature tensor for the spherical surface is calculated, resulting in a matrix with elements that include negative 'a' and terms involving sine and cosine squared.
- 🦄 For the torus, the process is similar, with the shift tensor and normal vector provided, and partial derivatives calculated for theta and phi.
- 🔗 The contraction for the torus results in a symmetric matrix, with elements that include 'a' and 'b', and terms involving sine and cosine squared.
- 📝 The final results for the curvature tensors of the cylindrical, spherical, and torus surfaces are summarized, providing a quick reference for future use.
Q & A
What is the main focus of video 75 of tensor calculus?
-The main focus of video 75 is to evaluate the curvature tensor for different sample surfaces using a specific formula derived from previous videos.
What are the two components that make up the formula used to evaluate the curvature tensor?
-The two components are the shift tensor and the partial derivatives of the normal with respect to the surface coordinates.
What is the first surface the video begins with for the curvature tensor evaluation?
-The video begins with the cylindrical surface for the curvature tensor evaluation.
What are the partial derivatives of the normal vector with respect to theta and z for a cylindrical surface?
-For a cylindrical surface, the partial derivatives with respect to theta are -sin(theta) for the first component, cos(theta) for the second, and zero for the third. With respect to z, all partial derivatives are zero since the components do not depend on z.
How does the contraction process work when combining the shift tensor and the partial derivatives?
-The contraction process involves multiplying each row of the shift tensor with each column of the matrix of partial derivatives, resulting in a 2x2 matrix.
What is the result of the contraction for the first element of the curvature tensor of the cylindrical surface?
-The first element of the curvature tensor for the cylindrical surface is -a, after factoring out the sine squared plus cosine squared which equals one, and applying the negative sign from the formula.
What is the shift tensor for the spherical surface in the video?
-The shift tensor for the spherical surface is not explicitly given in the transcript, but it is used in conjunction with the normal to evaluate the partial derivatives for the curvature tensor.
How are the partial derivatives of the normal vector for the spherical surface represented in the video?
-The partial derivatives for the spherical surface are represented as a matrix where the first row contains derivatives with respect to theta and the second row contains derivatives with respect to phi.
What is the final result for the curvature tensor of the spherical surface?
-The final result for the spherical surface includes elements such as -a, 0, 0, and -a * sin^2(theta), after performing the contraction and applying the necessary signs.
What is the significance of the curvature tensor being symmetric in the evaluation process?
-The symmetry of the curvature tensor implies that the element in the first row and second column is equal to the element in the second row and first column, allowing for time-saving during calculations.
What is the result for the curvature tensor of the torus, as presented in the video?
-The result for the torus includes elements such as -(a + b * cos(phi) * cos(phi)), 0, 0, and -b, after performing the contraction and considering the symmetry of the tensor.
Outlines
📚 Curvature Tensor Calculation for Cylindrical Surfaces
In this segment, the video script discusses the process of calculating the curvature tensor for a cylindrical surface using tensor calculus. The formula derived from a previous video is applied, which involves the shift tensor and partial derivatives of the normal vector with respect to surface coordinates. The script provides a step-by-step guide on evaluating partial derivatives with respect to theta and z, noting that for a cylindrical surface, the components do not depend on z, resulting in zero derivatives. The final step involves matrix contraction to obtain a 2x2 matrix, leading to the curvature tensor for the cylindrical surface, which is simplified to a single value due to the properties of sine and cosine squared.
🌐 Evaluating Curvature Tensor for Spherical Surfaces
This paragraph delves into the curvature tensor calculation for a spherical surface. The script outlines the process of evaluating partial derivatives of the normal vector with respect to theta and phi, and then performing a matrix contraction to find the tensor components. The common factor of cosine squared theta is factored out, simplifying the calculation, and the script highlights the symmetry of the resulting tensor, which helps in understanding the relationship between the elements. The final result for the spherical surface curvature tensor is presented, emphasizing the negative sign associated with the formula.
🐃 Calculating the Curvature Tensor for Taurus Surfaces
The script moves on to calculate the curvature tensor for a taurus surface, starting with filling out the matrix elements using partial derivatives of the normal vector with respect to theta and phi. The contraction process is then explained, with the script pointing out common factors and using the identity of sine squared plus cosine squared equals one to simplify the calculations. The script also notes the symmetry of the tensor, allowing for time-saving shortcuts in the calculation process. The final results for the taurus surface curvature tensor are presented, including the application of a negative sign to certain elements.
📋 Recap and Summary of Curvature Tensor Results
The final paragraph of the script serves as a recap and summary of the curvature tensor results for the three types of surfaces discussed: cylindrical, spherical, and taurus. It emphasizes the importance of understanding the symmetry of the tensor and provides a quick review of the results obtained for each surface. The script concludes with a reminder to the viewers about the process and invites them to join for the next video in the series.
Mindmap
Keywords
💡Curvature Tensor
💡Shift Tensor
💡Partial Derivatives
💡Normal Vector
💡Cylindrical Surface
💡Spherical Surface
💡Taurus
💡Matrix Contraction
💡Surface Coordinates
💡Differential Geometry
💡Symmetry
Highlights
Introduction of using a derived formula from the previous video to evaluate the curvature tensor for sample surfaces.
Explanation of the components of the curvature tensor, including the shift tensor and partial derivatives of the normal vector.
Beginning the evaluation with a cylindrical surface and presenting the shift tensor and normal vector.
Calculation of partial derivatives of the normal vector with respect to surface coordinates for the cylindrical surface.
Observation that none of the normal vector components depend on 'z' for the cylindrical surface, resulting in zero partial derivatives.
Combining elements with a contraction to form a 2x2 matrix for the curvature tensor of the cylindrical surface.
Result of the contraction showing a negative 'a' for the first element of the curvature tensor for the cylindrical surface.
Demonstration of the curvature tensor calculation for the spherical surface, including the shift tensor and normal vector.
Presentation of the partial derivatives matrix for the spherical surface, already calculated for time efficiency.
Formation of the contraction for the spherical surface and the resulting elements of the curvature tensor.
Result for the spherical surface showing a negative 'a' for the first element and a zero for the off-diagonal elements.
Transition to the torus surface with its shift tensor and normal vector for curvature tensor evaluation.
Display of the partial derivatives matrix for the torus surface, prepared in advance for the explanation.
Performance of the contraction for the torus surface and the calculation of its curvature tensor elements.
Result for the torus surface with a negative 'a' and 'b' for the diagonal elements and zeros for the off-diagonal elements.
Note on the symmetry of the curvature tensor, allowing for time-saving in calculations by recognizing equal elements.
Final results for all three surfaces: cylindrical, spherical, and torus, presented for reference.
Conclusion of the video with a summary of the curvature tensor results for the sample surfaces.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: