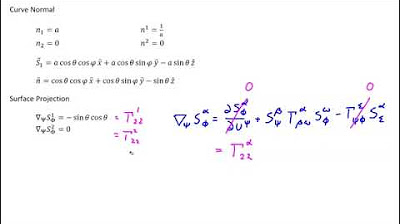Video 93 - Geodesic Curvature Tensor
TLDRThis video, part of a series on tensor calculus, introduces the geodesic curvature tensor, a crucial tool for analyzing curves on surfaces. The script explains the concept by drawing parallels with the surface normal, deriving its properties and formulas. It delves into the geometric interpretation, highlighting the differences between planar and curved surfaces. The video concludes with a decomposition of the vector curvature normal using the newly defined geodesic curvature tensor, providing insights into the curvature of curves relative to surfaces.
Takeaways
- 📚 The video introduces the concept of the geodesic curvature tensor, an essential tool for analyzing curves embedded in surfaces.
- 📐 The geodesic curvature tensor is analogous to the surface normal, which was previously introduced, and is represented using surface coordinates.
- 🔍 The normal to the curve does not lie on the curve itself, necessitating the use of surface coordinates and basis vectors for its representation.
- 📉 The video derives explicit formulas for the normal components by adapting previous formulas for the surface normal, adjusting for the reduced dimensionality.
- 📈 The normal is a unit vector with properties that include being orthogonal to the curve and lying in the tangent plane of the surface.
- 🔄 The geodesic curvature tensor is defined and its validity is confirmed by showing it is perpendicular to the curve, similar to the normal.
- 🔢 The video demonstrates that the geodesic curvature tensor is a second-rank symmetric tensor, a key property in tensor calculus.
- 📝 An expression is derived that relates the vector curvature normal to the surface curvature tensor and the geodesic curvature tensor, providing a way to decompose the vector curvature normal.
- 📉 The video highlights that for a plane surface, the geodesic curvature tensor simplifies, and the vector curvature normal is equivalent to the principal normal of the curve.
- 📚 The script concludes with a preview of applying these concepts with a specific example in a subsequent video.
Q & A
What is the main topic of this video in the series on tensor calculus?
-The main topic of this video is the introduction of the geodesic curvature tensor, an object used for analyzing curves embedded in surfaces.
What is the relationship between the geodesic curvature tensor and the normal to a curve?
-The geodesic curvature tensor is analogous to the normal of a curve, providing a way to analyze the curve's orientation in relation to the surface it is embedded in.
Why can't the normal to a curve be represented using the curve's coordinate?
-The normal to a curve does not lie on the curve itself, hence the surface coordinates must be used to represent it, as it is not intrinsic to the curve's coordinate system.
What properties does the normal to a curve share with the surface normal?
-Both the normal to a curve and the surface normal are unit vectors and are orthogonal to the respective geometric entity they are associated with (the curve or the surface).
How does the definition of the geodesic curvature tensor relate to the surface curvature tensor?
-The geodesic curvature tensor is defined through a covariant derivative of a shift tensor and is related to the surface curvature tensor through the chain rule for covariant derivatives.
What is the significance of the vector curvature normal in the context of this video?
-The vector curvature normal quantifies the curvature of the curve in relation to the ambient space and is decomposed into its normal and surface projections using the geodesic curvature tensor.
How does the script demonstrate that the geodesic curvature tensor is a valid definition?
-The script demonstrates the validity of the geodesic curvature tensor definition by showing that it is orthogonal to the curve, maintaining the properties of a normal vector.
What is the geometric interpretation of the geodesic curvature tensor in the context of a plane surface?
-In the case of a plane surface, the geodesic curvature tensor represents the curvature of the curve itself, as the plane curvature tensor vanishes, making the vector curvature normal equivalent to the principal normal.
Why is it important to show that the geodesic curvature tensor is a second-rank symmetric tensor?
-Showing that the geodesic curvature tensor is symmetric is important for understanding its mathematical properties and ensuring that it behaves as expected in tensor operations and calculations.
How does the script connect the vector curvature normal, the surface normal, and the geodesic curvature tensor in the final expression?
-The script connects these tensors by decomposing the vector curvature normal into its normal and surface projections, which are related to the surface normal and the geodesic curvature tensor, respectively.
Outlines
📚 Introduction to Geodesic Curvature Tensor
The script introduces the geodesic curvature tensor, a mathematical object crucial for analyzing curves on surfaces. It draws parallels with the previously discussed surface normal, highlighting the need to represent the normal using ambient coordinates. The video aims to explore the properties of this tensor in detail, starting with a review of the surface normal's properties and moving towards adapting the formulas for the new context of curves on surfaces.
🔍 Properties and Formulas of Geodesic Curvature
This paragraph delves into the properties of the geodesic curvature tensor, emphasizing its unit vector nature and orthogonality to the curve. It discusses the process of deriving explicit formulas for the tensor's components, which involves reducing the dimensionality of the previously known formulas for the surface normal. The paragraph also highlights the importance of adjusting the Levi-Civita symbols and other elements when the number of dimensions changes.
📐 Geometric Interpretation and Chain Rule Application
The script discusses the geometric interpretation of the geodesic curvature tensor, especially when dealing with curved surfaces. It clarifies the difference between the principal normal and the geodesic normal, noting that they generally point in different directions unless the surface is a plane. The paragraph also applies the chain rule for covariant derivatives to establish relationships between the curvature tensors and the covariant basis vectors.
🔧 Defining the Geodesic Curvature Tensor and Its Orthogonality
The geodesic curvature tensor is formally defined in this section, with an emphasis on proving its orthogonality to the curve. The script uses covariant derivatives and the properties of the shift tensor to demonstrate this orthogonality. It also establishes that the geodesic curvature tensor is a second-rank symmetric tensor, a key property for further analysis.
🌐 Relating Curvature Tensors and Decomposing Vector Curvature Normal
This paragraph focuses on the relationship between different curvature tensors, including the vector curvature normal, the surface curvature tensor, and the newly defined geodesic curvature tensor. It presents a comprehensive equation that relates these tensors and discusses the geometric meaning of each component. The script also explains how the surface normal and the geodesic normal are both perpendicular to the curve, providing a deeper understanding of their roles.
📘 Recap and Preview of Upcoming Concepts
The script concludes with a recap of the main points covered in the video, including the definition and properties of the geodesic curvature tensor, its relationship with other curvature tensors, and its geometric significance. It also previews the intention to demonstrate these concepts with a specific example in the next video, promising a practical application of the theoretical framework established.
Mindmap
Keywords
💡Geodesic Curvature Tensor
💡Surface Normal
💡Tangent Plane
💡Levi-Civita Symbol
💡Covariant Derivative
💡Christoffel Symbols
💡Vector Curvature Normal
💡Orthogonality
💡Second Rank Tensor
💡Projection
Highlights
Introduction of the geodesic curvature tensor, an essential tool for analyzing curves embedded in surfaces.
The geodesic curvature tensor is analogous to the surface normal, providing a new perspective on curves within a plane.
The normal to the curve is represented as a linear combination using ambient vector components, highlighting its relationship with the ambient basis vector.
Exploration of the properties of the geodesic curvature tensor in more detail, emphasizing its importance in tensor calculus.
Derivation of explicit formulas for the normal components, building upon previous work and adapting them to the current context.
Reduction of dimensionality in the formulas to accommodate the change from ambient to surface indexes, a key step in the analysis.
The geodesic curvature tensor is shown to have properties similar to the surface normal, including being a unit vector and orthogonal to the curve.
The distinction between the geometric interpretation of the normal on a plane versus a curved surface, clarifying the unique behavior of the geodesic curvature tensor.
The chain relationship between the normal, the covariant basis vector, and the covariant derivative, providing a deeper understanding of the tensor's behavior.
Introduction of the geodesic curvature tensor as a second rank symmetric tensor, with implications for its geometric interpretation.
Demonstration of the orthogonality of the geodesic curvature tensor to the curve, validating its definition and properties.
The decomposition of the vector curvature normal into its normal and surface projections, offering a new way to analyze curve curvature.
The relationship between the geodesic curvature tensor and the curvature of the curve in relation to the surface, providing a comprehensive view of curvature analysis.
The special case of a plane surface where the geodesic curvature tensor simplifies, revealing its equivalence to the curvature of the curve itself.
A recap of the video's content, summarizing the definition, properties, and significance of the geodesic curvature tensor in tensor calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: