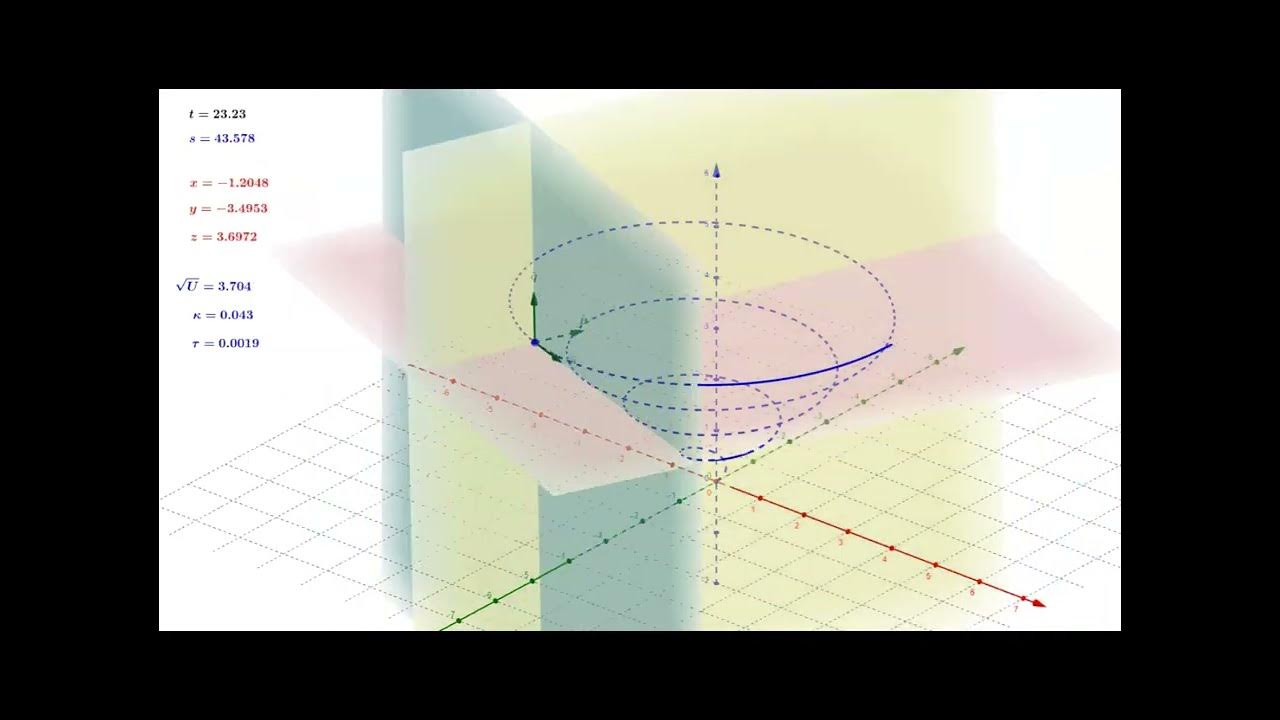
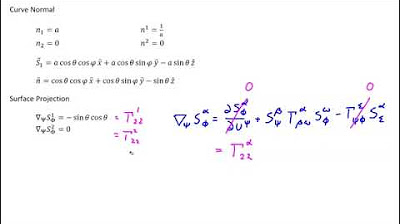Video 63 - The Normal
TLDRThis video, part of a series on tensor calculus, delves deeper into the properties of the normal vector, highlighting its orthogonality to both covariant and contravariant basis vectors. The video demonstrates that the normal remains unaffected by transformations between these bases, establishing it as a distinct vector. It further derives an explicit formula for the normal vector's components using the cross product of covariant basis vectors and the shift tensor, ultimately normalizing the resulting vector to ensure it's a unit vector, orthogonal to the tangent space.
Takeaways
- 📚 The video discusses the properties of the normal vector in tensor calculus, particularly its orthogonality to both covariant and contravariant basis vectors.
- 🔍 The script explains that the normal vector's properties can be expressed with a free index, which is raised by contracting with the contravariant metric tensor.
- 📉 The video demonstrates that the normal vector is unaffected by transformations between contravariant and covariant bases, indicating it is not part of the transformation.
- 📐 It is shown that the normal vector can be represented as a linear combination involving the covariant components and the contravariant basis vectors in the ambient space.
- 📝 The script derives an explicit formula for the vector components of the normal by taking the cross product of the covariant basis vectors S1 and S2.
- 📈 The cross product is explained as a vector operation that results in a vector orthogonal to the tangent plane, which aligns with the direction of the normal.
- 🧩 The video uses the shift tensor to express the cross product in tensor calculus syntax, leading to an expression for the normal vector components.
- ⚖️ The magnitude of the normal vector (W) is calculated, showing that it is equal to the square root of the determinant of the metric tensor (s).
- 📊 The normal vector is normalized to become a unit vector, which is essential for its definition as it must be orthogonal to the surface with a length of one.
- 🔄 The script also derives the contravariant component of the normal vector by raising the index, which is a standard tensor operation.
- 🔚 The video concludes with a recap of the normal vector properties and the derived expressions for both covariant and contravariant components.
Q & A
What are the two properties of the normal introduced in video 58?
-The normal is introduced with two properties: it is orthogonal to the covariant basis vectors and it has a unit length.
Why is the normal considered to be unaffected by the transformation between contravariant and covariant bases?
-The normal is unaffected by the transformation because it is not considered to be either contravariant or covariant; it does not have an index and does not participate in the transformation process.
How does the script demonstrate that the normal is orthogonal to both the covariant and contravariant basis vectors?
-The script demonstrates this by showing that the dot product of the normal with the covariant and contravariant basis vectors results in zero, indicating orthogonality.
What is the significance of the normal being orthogonal to the covariant and contravariant basis vectors?
-The significance is that the normal is perpendicular to the tangent plane defined by the basis vectors, which is a key property for defining the direction of the normal to a surface.
How is the cross product between the covariant basis vectors S1 and S2 related to the normal?
-The cross product of S1 and S2 produces a vector that is orthogonal to both S1 and S2, which lies in the direction of the normal.
What is the role of the shift tensor in deriving the expression for the normal?
-The shift tensor is used to express the covariant basis vectors as a linear combination of the ambient space basis vectors, which helps in deriving the expression for the normal.
Why is it necessary to normalize the vector resulting from the cross product of S1 and S2?
-Normalization is necessary to ensure that the resulting vector is a unit vector, which is a requirement for the normal as it defines both direction and magnitude.
How does the script use the permutation symbol to deal with the anti-symmetry of the indices in the cross product expression?
-The script uses the permutation symbol to capture the anti-symmetry of the indices, allowing for the simplification of the cross product expression by accounting for the sign changes when indices are swapped.
What is the final form of the expression for the normal derived in the script?
-The final form of the expression for the normal is derived by dividing the cross product of the covariant basis vectors by the square root of the determinant of the metric tensor, ensuring the normal is a unit vector orthogonal to the surface.
How does the script verify that the derived expression for the normal is indeed orthogonal to the basis vectors?
-The script verifies orthogonality by forming contractions with the basis vectors and showing that these contractions result in zero, confirming the normal's orthogonality.
Outlines
📚 Introduction to Normal Properties and Formula Derivation
This paragraph introduces the video's focus on tensor calculus, specifically the properties of the normal vector and deriving an explicit formula for its vector components. The normal's orthogonality to both covariant and contravariant basis vectors is discussed, highlighting that the normal is unaffected by transformations between these bases. The paragraph sets the stage for a deeper exploration of these properties and their implications.
🔍 Deep Dive into Normal Orthogonality and Basis Representation
The paragraph delves into the normal's orthogonality to the covariant and contravariant basis vectors, explaining the implications for the tangent space representation. It discusses how the normal's perpendicularity to these basis vectors is a result of their alignment with the tangent plane. The paragraph also explores the concept of using the normal in conjunction with the covariant and contravariant basis vectors to form a basis for the tangent space, emphasizing that the normal is not part of the transformation between these bases.
📘 Deriving the Cross Product of Basis Vectors for the Normal
This section outlines the process of deriving the normal vector through the cross product of covariant basis vectors S1 and S2. It references previous videos for the understanding of cross products and their properties, particularly their orthogonality to the input vectors. The paragraph introduces tensor calculus syntax for expressing the cross product and discusses the use of the shift tensor to represent the vector components of the basis vectors involved in the cross product.
🔢 Calculation of the Normal Vector's Magnitude
The paragraph focuses on calculating the magnitude of the normal vector derived from the cross product. It involves evaluating the dot product of the normal vector with itself in tensor calculus terms. The process includes raising the index of the normal vector components, using the shift tensor, and simplifying the expression to find the magnitude. The result is an expression for the magnitude of the normal vector, which is crucial for normalizing the vector.
🧲 Normalizing the Derived Vector and Finalizing the Normal Expression
After calculating the magnitude of the vector derived from the cross product, this paragraph describes the normalization process. It involves dividing the derived vector by its magnitude to obtain a unit normal vector. The final expression for the normal is presented, which is orthogonal to both S1 and S2 and has a unit length, fulfilling the definition of a normal vector.
🔚 Recap and Application of Normal Vector Properties
The final paragraph provides a recap of the video's main points, summarizing the understanding of the normal's properties and its derivation. It reiterates the normal's orthogonality to the basis vectors and its status as a vector unaffected by contravariant or covariant transformations. The paragraph also mentions the derived expressions for both the covariant and contravariant components of the normal vector and suggests exercises for further understanding. It concludes with a preview of applying these expressions to sample surfaces in the next video.
Mindmap
Keywords
💡Tensor Calculus
💡Normal Vector
💡Covariant Basis
💡Contravariant Basis
💡Orthogonality
💡Shift Tensor
💡Cross Product
💡Magnitude
💡Permutation Symbol
💡Unit Vector
💡Dot Product
Highlights
Introduction of the normal's properties in tensor calculus.
Exploration of the normal's orthogonality to both covariant and contravariant basis vectors.
Derivation of the normal's properties through index raising with the contravariant metric tensor.
Explanation of the normal's independence from contravariant and covariant basis transformations.
Discussion on the implications of the normal's orthogonality to the tangent plane.
Use of the shift tensor to express the normal in terms of linear combinations of basis vectors.
Demonstration of the normal's properties through equivalent forms involving the shift tensor.
Derivation of an explicit formula for the vector components of the normal.
Cross product between covariant basis vectors to find the normal direction.
Application of tensor calculus syntax to express the cross product.
Handling of anti-symmetric indexes in the cross product expression.
Isolation of the normal vector component using contraction with the permutation symbol.
Substitution of the permutation symbol with absolute tensors for simplicity.
Normalization of the derived vector to obtain the unit normal vector.
Calculation of the magnitude of the normal vector using tensor contraction.
Derivation of the normal vector's covariant and contravariant components.
Proof of the normal vector's orthogonality to the basis vectors through contraction.
Recap of the video's findings and the practical applications of the normal vector's properties.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: