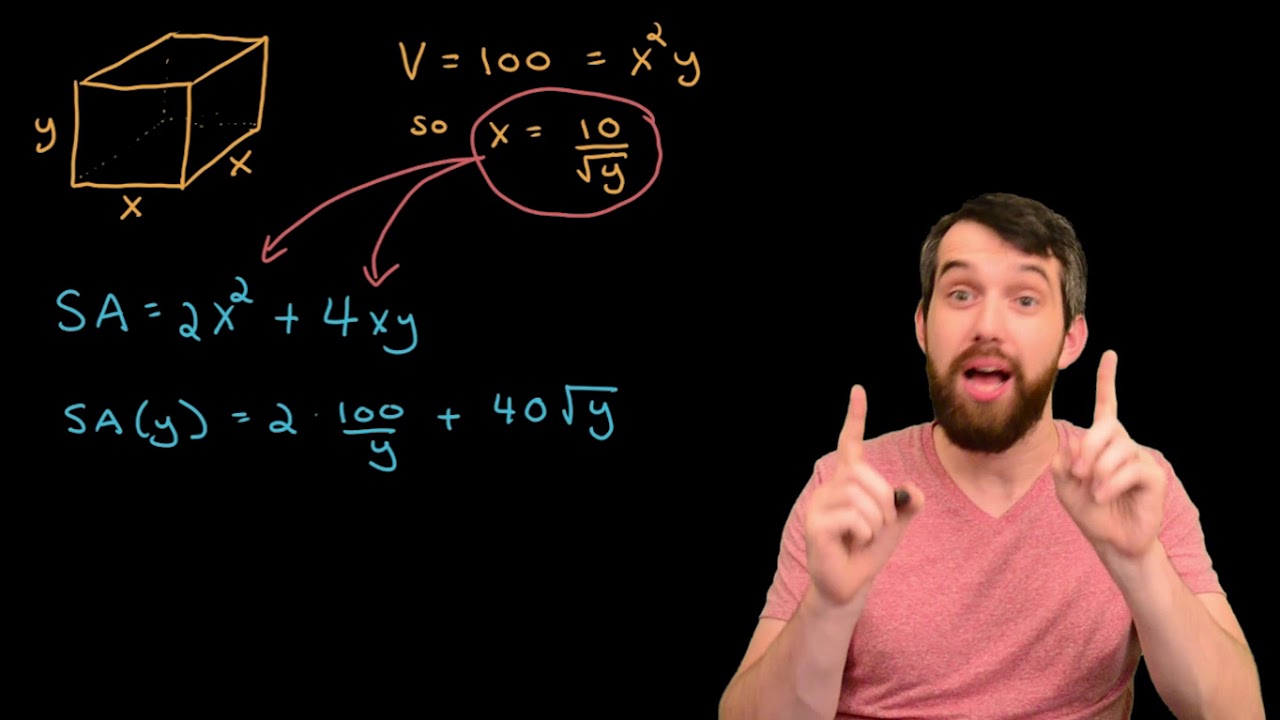Optimisation Grade 12: Maximum Surface Area Box

Kevinmathscience
21 May 202104:14
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the process of maximizing the surface area of a box with a given volume of 1000 cubic units, where the length is three times the breadth. The formula for surface area is derived and simplified using the volume constraint to express h in terms of x. The first derivative of the surface area function is taken to find the maximum value, which is achieved when x is approximately 6.06, indicating the optimal breadth for the box.

Takeaways
  • 📏 The problem is to find the value of x for a box that maximizes surface area, given a specific relationship between length and breadth.
  • 📐 The length of the box is three times the breadth, so if the breadth is x, the length is 3x.
  • 🏢 The surface area of the box is calculated by considering all the external faces, including the top, bottom, front, and sides.
  • 📉 The formula for surface area is simplified to 8hx + 6x^2, where h is the height and x is the breadth.
  • 🔄 To eliminate one variable, the volume of the box is related to the surface area by the given volume of 1000 cubic units.
  • 🧩 The volume formula is 3x^2 * h, and by setting it equal to 1000, h can be expressed as 1000 / (3x^2).
  • 🔍 Substituting h in the surface area formula with 1000 / (3x^2) allows for the expression of surface area solely in terms of x.
  • 📝 The resulting surface area equation is 8000x / (3x^2) + 6x^2, which simplifies to 8000/3x + 6x^2.
  • 🤔 To find the maximum surface area, the first derivative of the surface area equation with respect to x is taken and set to zero.
  • ✏️ The derivative simplifies to -8000/3x^3 + 12x, which is then set to zero to solve for x.
  • 🔑 The solution to the equation 8000 = 36x^3 yields x as the cube root of (8000/36), which is approximately 6.06.
Q & A

  • What is the main objective of the problem presented in the script?

    -The main objective is to find the value of x that maximizes the surface area of a box with a given volume and a specific relationship between its length and breadth.

  • What is the relationship between the length and breadth of the box as described in the script?

    -The length of the box is three times the breadth. If the breadth is x, then the length is 3x.

  • What is the formula for the surface area of the box given in the script?

    -The formula for the surface area is 2(h * x) + 6x^2 + 2(3x * h), which simplifies to 8hx + 6x^2.

  • How is the volume of the box related to the variables x and h in the script?

    -The volume of the box is given by the product of its length, breadth, and height, which is 3x^2 * h, and it is set to be equal to 1000 cubic units.

  • What substitution is made to eliminate one of the variables in the surface area formula?

    -The substitution made is to express h in terms of x using the volume formula, resulting in h = 1000 / (3x^2).

  • How is the surface area formula simplified after substituting for h?

    -After substituting for h, the surface area formula is simplified to 8000x / (3x) + 6x^2, which further simplifies to 8000/3x + 6x^2.

  • What mathematical method is used to find the maximum surface area?

    -The method used to find the maximum surface area is calculus, specifically by taking the first derivative of the surface area formula and setting it equal to zero.

  • What is the first derivative of the simplified surface area formula?

    -The first derivative is -8000/(3x^2) + 12x, which is obtained by differentiating the simplified surface area formula with respect to x.

  • How is the equation set up to find the maximum surface area after taking the derivative?

    -The equation is set up by equating the first derivative to zero: 0 = -8000/(3x^2) + 12x.

  • What is the final step in solving for x to find the maximum surface area?

    -The final step is to solve the equation 8000 = 36x^3 for x, which involves dividing both sides by 36 and then taking the cube root of the result.

  • What is the final answer for the value of x that maximizes the surface area?

    -The final answer for the value of x is approximately 6.06, which is obtained by taking the cube root of 8000/36.

Outlines
00:00
📚 Maximizing Surface Area of a Box

The script begins by setting up a mathematical problem to find the value of x that maximizes the surface area of a box. It's given that the length of the box is three times its breadth, and the breadth is represented by x. The script then derives the formula for the surface area of the box, considering all sides including the top and bottom. The volume of the box is also given as a thousand cubic units, leading to an equation that relates the volume to the dimensions of the box. The script proceeds to solve for the height (h) in terms of x and substitutes this back into the surface area formula, resulting in a single-variable equation in terms of x. The goal is to find the maximum surface area, which involves taking the derivative of the surface area equation with respect to x and setting it to zero to find critical points. The process involves algebraic manipulation to isolate x, ultimately leading to the solution for x that maximizes the surface area.

Mindmap
Keywords
💡Surface Area
Surface area refers to the total area that the surface of an object occupies. In the context of the video, the focus is on finding the dimensions of a box that maximize its surface area. The script mentions calculating the surface area by summing the areas of all the sides of the box, which includes the top, bottom, front, and sides.
💡Optimization
Optimization is the process of finding the best solution to a problem, often by maximizing or minimizing a particular value. In the video, the goal is to optimize the surface area of a box with a given volume, which is a classic example of an optimization problem in mathematics.
💡Box Dimensions
Box dimensions refer to the length, breadth, and height of a box. The script specifies that the length is three times the breadth, which is a constraint used to define the relationship between the dimensions of the box in the optimization problem.
💡Volume
Volume is the amount of space an object occupies, typically measured in cubic units. In the script, the volume of the box is given as a constant value (1000 cubic units), and it is used to derive a relationship between the height and the square of the breadth.
💡First Derivative
The first derivative of a function measures the rate at which the function is changing at any given point. In the video, the first derivative is used to find the critical points of the surface area function, which are potential maxima or minima.
💡Critical Points
Critical points are points on a graph where the derivative is zero or undefined, indicating potential maxima, minima, or points of inflection. The script involves setting the first derivative of the surface area function to zero to find the critical points.
💡Maximization
Maximization is the process of making a value as large as possible. In the context of the video, maximization is applied to the surface area of the box, with the aim of finding the dimensions that yield the largest possible surface area given the volume constraint.
💡Constraints
Constraints are limitations or conditions that restrict the solution space of a problem. In the script, the constraint is that the length of the box is three times the breadth, which limits the possible dimensions of the box.
💡Cubic Units
Cubic units are units of volume, such as cubic meters or cubic centimeters. The script uses cubic units to express the volume of the box, which is a key parameter in the optimization problem.
💡Third Root
The third root of a number is a value that, when multiplied by itself three times, gives the original number. In the script, the third root is used to solve for the breadth of the box after finding a cubic equation.
💡Calculus
Calculus is a branch of mathematics that deals with rates of change and accumulation. The video uses concepts from calculus, such as derivatives, to solve the optimization problem involving the surface area of the box.
Highlights

The goal is to find the value of x that maximizes the surface area of a box.

The box has a length that is three times the breadth.

Surface area includes the top, bottom, front, back, and sides of the box.

The surface area formula is derived as 2(h*x) + 6x^2 + 6xh.

The volume of the box is given as 1000 cubic units.

Volume formula is length * breadth * height = 3x^2 * h.

Solving for h gives h = 1000 / (3x^2).

Substitute h in the surface area formula using the volume relationship.

Simplify the surface area formula to 8000/(3x) + 6x^2.

To find maximum surface area, take the first derivative and set it to zero.

Derivative of the surface area formula is -8000/(3x^2) + 12x.

Solve the derivative equation to find critical points.

Simplify the derivative equation to 8000 = 36x^3.

Divide both sides by 36 to isolate x^3.

Take the cube root of both sides to solve for x.

The final answer for x is 6.06, which maximizes the surface area.

Transcripts

Browse More Related Video

Optimization Example: Minimizing Surface Area Given a Fixed Volume

Optimisation Grade 12: Maximum Surface Area Cylinder

Optimisation Grade 12: Maximum Volume Box

Optimisation Grade 12: Maximum Volume Cylinder

Optimization: Minimizing Surface Area of a Can

Optimization Cylinder Problem

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
OptimizationGeometrySurface AreaVolume ConstraintMaximizationCalculusDerivativeFirst DerivativeMath ProblemBox Design