02 - Fundamental Theorem of Calculus, Part 1 - Learn Antiderivatives & Derivatives
TLDRIn this calculus tutorial, Jason introduces the fundamental theorem of calculus, emphasizing its importance in calculating integrals. He explains that for a continuous function, the integral from 'a' to 'b' is found by evaluating the antiderivative at the upper limit and subtracting it at the lower limit. Jason illustrates the concept with simple examples, showing how to find antiderivatives for basic functions and emphasizing the relationship between derivatives and antiderivatives. The lesson sets the stage for further practice and techniques in integration.
Takeaways
- 📚 The Fundamental Theorem of Calculus is a central concept that provides a method for calculating integrals.
- 🔍 A function must be continuous over the interval [a, b] for integration to be valid, ensuring no jumps or discontinuities in the function.
- 📈 The antiderivative, denoted by capital F, is a function that, when differentiated, yields the original function f(x).
- 📝 The integral of a function from a to b is equal to the antiderivative evaluated at b minus the antiderivative evaluated at a, as per the Fundamental Theorem of Calculus.
- 📉 The process of finding the antiderivative involves reversing the process of differentiation to regain the original function.
- 📌 Examples given in the script illustrate how to find antiderivatives for simple functions like 3x, 1/2x^2, and sine(x).
- 📐 The derivative of the antiderivative should return the original function, showing the inverse relationship between differentiation and antiderivatives.
- 📊 Definite integrals have limits of integration and return a numerical value, representing the area under the curve between two points.
- 📘 Indefinite integrals do not have specified limits and return a function, which is the antiderivative of the original function.
- 🔑 The script emphasizes the importance of understanding antiderivatives as they are crucial for solving integrals, whether definite or indefinite.
- 📚 The session aims to provide a foundational understanding before diving into techniques for finding antiderivatives and solving more complex integral problems.
Q & A
What is the main topic of the video script?
-The main topic of the video script is the Fundamental Theorem of Calculus, which is a crucial concept in calculus for calculating integrals.
What is the significance of the Fundamental Theorem of Calculus?
-The Fundamental Theorem of Calculus is significant because it provides a method to calculate integrals by evaluating antiderivatives at the limits of integration.
What is a continuous function in the context of calculus?
-A continuous function in calculus is a function that has no jumps or breaks in its graph; it has a smooth curve without any discontinuities.
What is an antiderivative and how is it related to the derivative of a function?
-An antiderivative is a function that, when differentiated, yields the original function. It is the reverse process of finding the derivative.
How does the Fundamental Theorem of Calculus relate to finding the area under a curve?
-The Fundamental Theorem of Calculus states that the integral from a to b of a function f(x) is equal to the antiderivative of f(x) evaluated at b minus the antiderivative evaluated at a, which represents the area under the curve from a to b.
What is the difference between a definite integral and an indefinite integral?
-A definite integral has limits of integration and returns a numerical value, representing the area under the curve between those limits. An indefinite integral does not have limits and returns a function, which is the antiderivative of the original function.
What is the antiderivative of the function f(x) = 3?
-The antiderivative of the function f(x) = 3 is F(x) = 3x, because the derivative of 3x is 3, which is the original function.
Can you provide an example of finding the antiderivative of a function and then using it to calculate a definite integral?
-Yes, for example, if you have the function f(x) = x, the antiderivative is F(x) = 1/2 * x^2. To calculate the definite integral from 1 to 4, you would evaluate F(4) - F(1), which gives (1/2 * 4^2) - (1/2 * 1^2) = 8 - 0.5 = 7.5.
What is the derivative of the antiderivative of a function?
-The derivative of the antiderivative of a function is the original function itself. This is because antiderivatives and derivatives are inverse operations.
Why is it important to understand antiderivatives when learning about the Fundamental Theorem of Calculus?
-Understanding antiderivatives is important because they are the key to applying the Fundamental Theorem of Calculus. Without knowing the antiderivative, you cannot evaluate the integral and find the area under the curve or perform other related calculations.
What are some techniques that will be taught later in the course to find antiderivatives of more complex functions?
-The script mentions that the course will cover various techniques developed over the years to find antiderivatives of complex functions. These techniques will help students identify the problem type and figure out how to calculate the integrals.
Outlines
📚 Introduction to the Fundamental Theorem of Calculus
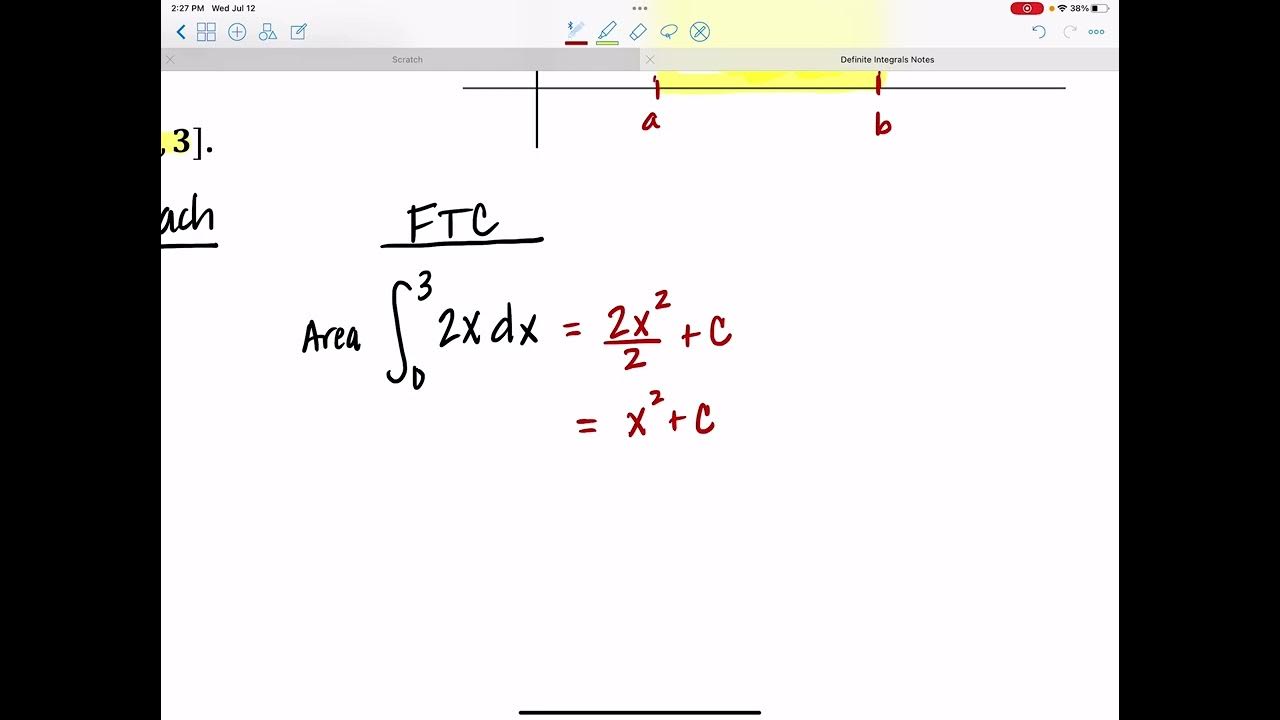
Jason introduces the concept of the Fundamental Theorem of Calculus, emphasizing its importance in calculus. He explains that the theorem is the key to calculating integrals and provides a basic understanding of what an integral represents. The discussion includes the prerequisites for integration: a continuous function over an interval [a, b]. Jason also introduces the concept of an antiderivative, denoted by capital F, which is crucial for evaluating definite integrals. He illustrates the theorem with a graphical representation, explaining how the area under a curve can be found by evaluating the antiderivative at the upper and lower limits of integration.
🔍 Understanding Antiderivatives and Derivatives
This paragraph delves deeper into the concept of antiderivatives, contrasting them with derivatives. Jason uses the analogy of opposites to explain the relationship between a function and its antiderivative. He provides several examples to demonstrate how to find antiderivatives for simple functions, such as constants, linear functions, and the cosine function. The explanation includes the process of taking the derivative of the antiderivative to verify that it returns to the original function, reinforcing the concept that antiderivatives and derivatives are inverse operations in calculus.
📉 Definite and Indefinite Integrals: Definitions and Differences
Jason clarifies the distinction between definite and indefinite integrals. A definite integral has specified limits of integration and yields a numerical result, as demonstrated with the example of integrating the constant function 3 from 1 to 4. On the other hand, an indefinite integral does not have limits and results in a function, the antiderivative. He emphasizes that while the process of finding the antiderivative is the same for both types of integrals, the application and the final result differ significantly. This distinction is crucial for understanding how to apply the fundamental theorem of calculus in various contexts.
🎯 Applying the Fundamental Theorem of Calculus in Practice
In the final paragraph, Jason looks forward to applying the Fundamental Theorem of Calculus through practical examples. He acknowledges that while the current discussion has been conceptual, the subsequent sections will focus on problem-solving and mastering the techniques required to find antiderivatives for more complex functions. He assures the audience that there will be ample practice to solidify their understanding and ability to calculate integrals using the theorem. The goal is to transition from foundational concepts to a deep understanding of integral calculation through hands-on application.
Mindmap
Keywords
💡Fundamental Theorem of Calculus
💡Integral
💡Antiderivative
💡Continuous Function
💡Derivative
💡Definite Integral
💡Indefinite Integral
💡Limits of Integration
💡Area Under the Curve
💡Calculus
Highlights
Introduction to the fundamental theorem of calculus, a key concept in calculus for calculating integrals.
Explanation of the integral as a representation of the area under a curve, motivating the concept before delving into calculations.
Requirement for a function to be continuous on an interval for integration, ensuring no jumps or discontinuities.
Introduction of the antiderivative, denoted by capital F, as the function that, when differentiated, returns the original function.
The fundamental theorem of calculus formula: integral from a to b of f(x) dx equals F(b) - F(a), illustrating how to calculate integrals.
Visual representation of the integral as the area under a curve, with a practical example of a function and its antiderivative.
Explanation of antiderivatives as functions that, when differentiated, yield the original function, using a step-by-step example.
Demonstration of finding antiderivatives for simple functions like 3x, x, and cosine(x), showcasing the process of integration.
Clarification that antiderivatives and derivatives are opposites, with the antiderivative leading back to the original function upon differentiation.
Introduction of definite integrals, which have limits and return a numerical value representing the area under the curve.
Example of a definite integral calculation, showing the process of evaluating the antiderivative at the limits of integration.
Contrast between definite and indefinite integrals, with the latter lacking limits and returning a function rather than a number.
Emphasis on the importance of understanding antiderivatives as the core of integration, with techniques to be explored in subsequent lessons.
Acknowledgment of the difficulty in finding antiderivatives for complex functions, indicating the need for developed techniques.
Teaching approach that focuses on definitions and fundamentals before moving on to problem-solving practice with various types of integrals.
Promise of upcoming sections that will provide practical application of the fundamental theorem of calculus through problem-solving.
Conclusion of the lesson with a summary of the importance of antiderivatives and the fundamental theorem of calculus in integration.
Transcripts
Browse More Related Video

Definite Integrals!

Fundamental Theorem of Calculus Parts 1&2

Calculus AB/BC – 6.4 The Fundamental Theorem of Calculus and Accumulation Functions

Fundamental Thereom of Calculus Explained - Part 1 & 2 Examples - Definite Integral

Area between a curve and the x-axis | AP Calculus AB | Khan Academy
Definite Integrals
5.0 / 5 (0 votes)
Thanks for rating: