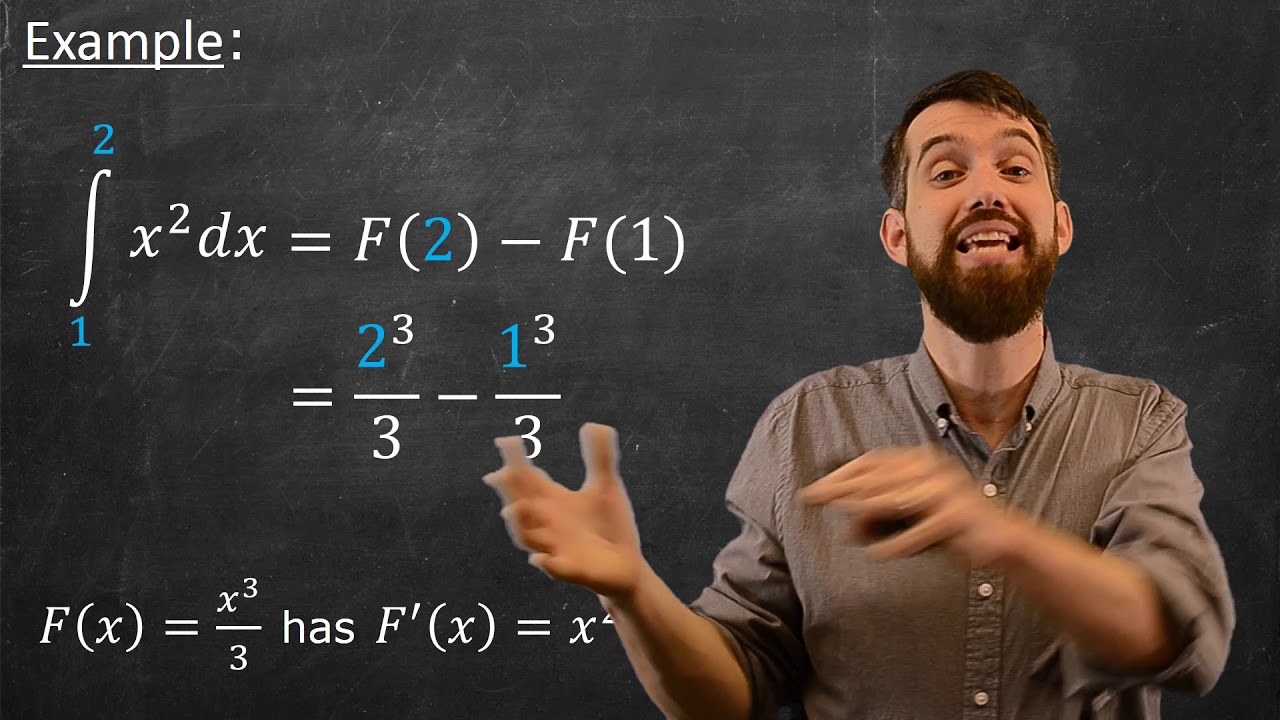Area between a curve and the x-axis | AP Calculus AB | Khan Academy

Khan Academy
24 Jan 201305:53
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the concept of finding the exact area under a curve using definite integrals, specifically for the function f(x) = x^2 between x=1 and x=4. It introduces the fundamental theorem of calculus, part two, which relates antiderivatives to definite integrals. The process involves identifying the antiderivative of f(x), calculating it at the upper and lower bounds of integration, and finding the difference. The result is the area, given in square units, which in this case is 21.

Takeaways
  • 📈 The function in focus is f(x) = x^2, representing a curve in the first quadrant.
  • 🔍 The area of interest is under the curve of f(x) = x^2, above the positive x-axis, between x=1 and x=4.
  • 🎯 To find the exact area, the definite integral is used, denoted as ∫ from 1 to 4 of f(x) dx.
  • 🏞️ The concept of the definite integral involves summing the areas of infinitesimally thin rectangles under the curve.
  • 📚 The Riemann sum is a way to conceptualize the definite integral, by summing the areas of small rectangles.
  • 🌟 The second fundamental theorem of calculus is key to evaluating the definite integral when an antiderivative is known.
  • 🔄 The antiderivative of f(x) is a function F(x) such that the derivative of F(x) equals f(x).
  • 📌 For the function f(x) = x^2, the antiderivative F(x) is x^3/3, derived from the power rule.
  • 🧮 The area is calculated by evaluating F(x) at the upper limit (4) and subtracting the value at the lower limit (1).
  • 🔢 The final calculated area is 21 square units, by computing (4^3/3) - (1^3/3) and simplifying the result.
  • 📈 This process demonstrates the practical application of calculus in determining areas under curves for specific intervals.
Q & A

  • What is the function being discussed in the transcript?

    -The function being discussed is f(x) = x^2.

  • What is the main concern of the speaker in the transcript?

    -The speaker is concerned with finding the exact area under the curve of the function f(x) = x^2 between x = 1 and x = 4.

  • How is the area under the curve represented?

    -The area under the curve is represented using the definite integral from 1 to 4 of f(x) dx.

  • What is the conceptual basis for the definite integral?

    -The conceptual basis for the definite integral is the summation of an infinite number of infinitely thin rectangles, which is reminiscent of a Riemann sum.

  • What is the Second Fundamental Theorem of Calculus?

    -The Second Fundamental Theorem of Calculus states that if a function f has an antiderivative, then the definite integral of f from a to b is equal to the antiderivative evaluated at b minus the antiderivative evaluated at a.

  • How does one find the antiderivative of f(x) = x^2?

    -The antiderivative of f(x) = x^2 is F(x) = (x^3)/3, which is found using the power rule for integration.

  • What is the value of the definite integral of x^2 from 1 to 4?

    -The value of the definite integral of x^2 from 1 to 4 is 21 square units.

  • How does the speaker calculate the area under the curve?

    -The speaker calculates the area by evaluating the antiderivative (x^3)/3 at 4 and subtracting the value of the antiderivative evaluated at 1.

  • What is the significance of the antiderivative in finding the area under the curve?

    -The antiderivative is significant because it allows for the calculation of the area under the curve through the Second Fundamental Theorem of Calculus, without the need for approximating areas with infinite rectangles.

  • What is the connection between the Riemann sum and the definite integral?

    -The connection is that the Riemann sum is the concept of summing up infinite rectangles of infinitesimally small width (dx) under the curve, which is the basis for the definite integral.

  • What is the role of the power rule in finding the antiderivative of f(x) = x^2?

    -The power rule is used to determine that the antiderivative of x^2 is (x^3)/3, by applying the rule that the integral of x^n with respect to x is (x^(n+1))/(n+1), and then simplifying.

Outlines
00:00
📊 Calculating the Area Under a Curve Using Definite Integrals

This paragraph discusses the process of finding the exact area under the curve of a function, specifically f(x) = x^2, between x = 1 and x = 4. The concept of definite integrals is introduced as a way to calculate this area, which involves summing up an infinite number of infinitely thin rectangles. The explanation includes a visual description of the function graphed in the first quadrant and the geometric interpretation of the definite integral as a Riemann sum. It also mentions the second fundamental theorem of calculus, which states that if a function has an antiderivative, the definite integral can be computed by evaluating the antiderivative at the upper limit of integration and subtracting its value at the lower limit.

05:02
🔢 Applying the Power Rule to Find the Antiderivative of x^2

The second paragraph focuses on the practical application of the power rule to find the antiderivative of the function f(x) = x^2. It explains that the antiderivative, denoted as F(x), is x^3/3. The process involves taking the derivative of x^3 and applying the power rule, which results in x^2. The explanation includes a step-by-step breakdown of the calculation, leading to the evaluation of the antiderivative at the bounds of integration (x = 4 and x = 1). The final step is to calculate the area by evaluating F(x) at 4 and subtracting the value at 1, resulting in an area of 21 square units for the region under the curve and above the x-axis between x = 1 and x = 4.

Mindmap
Keywords
💡Function
In the context of the video, a function is represented as f(x) = x^2, which is a mathematical relationship that assigns a unique output value to each input value x. The function is the primary focus of the video, as it is the curve whose area under the x-axis between x=1 and x=4 is being calculated. The graph of the function in the first quadrant is used to visualize the area of interest.
💡Area under the curve
The area under the curve refers to the region enclosed by the curve of a function, the x-axis, and the vertical lines x=a and x=b (in this case, a=1 and b=4). This area is of interest in integral calculus and can be calculated using the concept of definite integrals. The video's main objective is to find this exact area for the given function f(x) = x^2 between x=1 and x=4.
💡Definite integral
A definite integral is a fundamental concept in calculus that represents the signed area under a curve between two points on the x-axis. It is denoted by the symbol ∫ and is used to calculate the exact area of a shape formed by the curve, the x-axis, and the vertical lines x=a and x=b. In the video, the definite integral is used to find the area under the curve of the function f(x) = x^2 between x=1 and x=4.
💡Infinite rectangles
In the video, the concept of infinite rectangles is used to visualize the process of calculating a definite integral. These rectangles are imagined as having an infinite number of them and being infinitely thin, with their widths representing an infinitesimally small change in x (dx) and their heights equal to the function's value at that x. The area under the curve is approximated by summing the areas of these rectangles, which is a conceptual basis for the Riemann sum and the definite integral.
💡Riemann sum
The Riemann sum is a method used to approximate the definite integral by dividing the area under the curve into small rectangles and summing their areas. It is closely related to the concept of definite integrals and provides an intuitive understanding of how integrals work. The video uses the idea of Riemann sums to explain how the area under the curve can be approximated by summing the areas of rectangles before moving on to the exact calculation using definite integrals.
💡Antiderivative
An antiderivative, also known as an indefinite integral, is a function whose derivative is the given function. In the context of the video, finding the antiderivative of f(x) = x^2 is crucial for calculating the definite integral using the Fundamental Theorem of Calculus. The antiderivative is used to evaluate the area under the curve by finding the difference between its values at the bounds of integration.
💡Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus is a key result that connects the concepts of differentiation and integration. It states that if a function is continuous on a closed interval [a, b] and has an antiderivative on that interval, then the definite integral of the function over that interval can be calculated as the difference between the antiderivative's values at the endpoints of the interval. In the video, this theorem is used to find the exact area under the curve y=f(x) = x^2 between x=1 and x=4.
💡Power rule
The power rule is a basic differentiation rule in calculus that states if f(x) = x^n, where n is a constant, then the derivative of f with respect to x is n*x^(n-1). This rule is used in the video to find the antiderivative of f(x) = x^2, which is x^3/3, by taking the derivative of x^3 and dividing by 3 to get back to the original function.
💡Evaluation
In the context of the video, evaluation refers to the process of finding the value of a function or an antiderivative at specific points within the domain. This is necessary for calculating the definite integral using the antiderivative, as it involves finding the difference in the values of the antiderivative at the bounds of integration (in this case, at x=4 and x=1).
💡Subtraction
Subtraction is a basic arithmetic operation used in the video to calculate the difference between the values of the antiderivative at the upper and lower bounds of the interval of integration. This difference gives the value of the definite integral, which in the case of the video, represents the area under the curve y=f(x) = x^2 between x=1 and x=4.
💡Square units
Square units refer to a unit of measurement for area, where one unit is the square of the standard linear unit (such as meters or feet). In the context of the video, the area under the curve is expressed in these units, with the final calculation showing that the area is 21 square units.
Highlights

The function f(x) is defined as x squared.

The area under the curve of y = f(x) from x=1 to x=4 is to be calculated.

The definite integral is used to denote the exact area under the curve.

The concept of summing an infinite number of infinitely thin rectangles is introduced to approximate the area.

The Riemann sum is mentioned as the basis for the concept of the definite integral.

The second fundamental theorem of calculus is key to calculating the definite integral.

If f has an antiderivative, the definite integral can be evaluated by finding the antiderivative and subtracting its value at the lower limit from its value at the upper limit.

The antiderivative of f(x) = x^2 is F(x) = (x^3)/3, derived using the power rule.

The process of evaluating the antiderivative at the upper limit (4) and subtracting its value at the lower limit (1) is described.

The antiderivative F(x) = (x^3)/3 is confirmed to be correct by taking the derivative and matching f(x).

The area under the curve is calculated to be 63/3 or 21 square units.

The method for calculating the area under a curve using definite integrals and antiderivatives is clearly explained.

The practical application of the second fundamental theorem of calculus in finding exact areas is demonstrated.

The mathematical process of evaluating antiderivatives and applying them to find areas is thoroughly detailed.

The use of the power rule in determining the antiderivative of a function is highlighted.

The importance of the concept of the definite integral in calculus for solving real-world problems is emphasized.

The transcript provides a step-by-step guide on how to apply the fundamental theorem of calculus to find the area under a curve.

Transcripts

Browse More Related Video

Area between curves with multiple boundaries

Fundamental Theorem of Calculus II

Definite Integrals!

Area Between y=x^3 and y=3x-2 | MIT 18.01SC Single Variable Calculus, Fall 2010

Calculus - Definite Integrals

Fundamental theorem of calculus (Part 2) | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusIntegralsArea CalculationMathematicsEducationTheoreticalRiemann SumAntiderivativePower Rule