Fundamental Thereom of Calculus Explained - Part 1 & 2 Examples - Definite Integral
TLDRThis video script offers an in-depth exploration of the Fundamental Theorem of Calculus, Parts 1 and 2, through a series of illustrative examples. It begins by defining the concept of antiderivatives and their relationship with continuous functions on specific intervals. The video then demonstrates how to apply Part 1 of the theorem to find the derivative of an integral by substituting variables and differentiating. Moving on to Part 2, the script explains how to calculate the integral of a function over a closed interval by evaluating its antiderivative at the endpoints and subtracting. The video provides a step-by-step walkthrough of several problems, showing how to simplify complex integrals and find their derivatives efficiently. It covers a range of functions, from polynomials to trigonometric and logarithmic expressions, showcasing the versatility of the theorem in solving calculus problems. The script emphasizes the power of the theorem in both simplifying the integration process and validating answers through differentiation. The video concludes by reinforcing the two-part theorem's significance in calculus, highlighting its role in connecting integration and differentiation as inverse processes. It encourages viewers to practice both the quick methods and the detailed problem-solving approach to gain a comprehensive understanding of the subject.
Takeaways
- 📚 The Fundamental Theorem of Calculus (Part 1) states that the derivative of an antiderivative G(x) is equal to the original function F(x), showing integration and differentiation are inverse processes.
- 📈 G(x) represents the area under the curve of a function F(t) between points 'a' and 'x', and is a continuous function on the interval 'a' to 'x'.
- 🌟 To find the derivative of an integral, replace the variable 't' with 'x' and multiply by the derivative of the upper limit of integration.
- 🔄 The process of finding the derivative of an integral involves differentiating the integrand with respect to the variable of integration, and then applying the limits of integration.
- 📊 If the lower limit of integration is a function of 'x', replace 't' with that function and include a negative sign to account for the derivative of the lower limit.
- 🌐 For more complex integrals, distribute the integrand if necessary before applying the rules of differentiation.
- 📚 The Fundamental Theorem of Calculus (Part 2) states that if F(x) is continuous on 'a' to 'b', then the integral of F(x) from 'a' to 'b' is F(b) - F(a).
- 🔢 To evaluate a definite integral, find the antiderivative F(x), then evaluate it at the upper and lower limits and subtract.
- 📈 The antiderivative of a function F(x) is denoted as F(x) and can be found by applying the rules of integration.
- 🌟 The process of integration and differentiation is cyclic; knowing one allows you to find the other, which is crucial for solving calculus problems.
- 📊 Practice is essential for mastering the techniques of finding derivatives of integrals and applying the Fundamental Theorem of Calculus effectively.
Q & A
What is the main topic of the video?
-The main topic of the video is the Fundamental Theorem of Calculus, specifically Part 1 and Part 2, and how to apply them to solve calculus problems involving integration and differentiation.
What does the function g(x) represent in the context of the video?
-In the context of the video, g(x) represents a function that tells you the area under the curve between two points, specifically between points 'a' and 'x'.
How is g(x) related to f(x) according to the Fundamental Theorem of Calculus Part 1?
-According to the Fundamental Theorem of Calculus Part 1, g'(x), the derivative of g(x), is equal to f(x). This shows that integration and differentiation are inverse processes of each other.
What is the significance of the function being continuous on the interval a to b?
-If f is a continuous function on the interval a to b, it ensures that g(x) will be a continuous function on the closed interval a to b and differentiable on the open interval a to b, which is necessary for applying the Fundamental Theorem of Calculus.
How does the video demonstrate the application of the Fundamental Theorem of Calculus?
-The video demonstrates the application of the Fundamental Theorem of Calculus by working through several examples where the derivative of the integral of a function is found by replacing the variable of integration with the variable of differentiation.
What is the conclusion of the Fundamental Theorem of Calculus Part 2?
-The conclusion of the Fundamental Theorem of Calculus Part 2 is that if a function f is continuous on the closed interval [a, b], then the definite integral of f from a to b is equal to the difference of the antiderivative F evaluated at b and a, i.e., ∫[a, b] f(x) dx = F(b) - F(a).
How does the video explain the process of finding the antiderivative of a function?
-The video explains the process of finding the antiderivative by showing how to apply the rules of differentiation in reverse. It demonstrates this by taking the derivative of the integral of a function and replacing the variable of integration with the variable of differentiation to find the original function.
What is the method used in the video to quickly find the derivative of an integral?
-The method used in the video to quickly find the derivative of an integral is to directly replace the variable of integration with the variable of differentiation and then multiply by the derivative of the variable that was replaced.
How does the video handle a problem where the lower limit is not zero?
-When the lower limit is not zero, the video shows that the negative of the lower limit's value must be used in the calculation. This is because the integral from the lower limit to the upper limit and the integral from the upper limit to the lower limit will have opposite signs.
What is the significance of the chain rule in the examples given in the video?
-The chain rule is significant in the examples given in the video as it is used to differentiate nested functions. This is particularly important when the function being integrated is a composite function, and the derivative must be taken with respect to the innermost function first.
How does the video address the concept of antiderivatives for trigonometric functions?
-The video addresses the concept of antiderivatives for trigonometric functions by showing how to find the antiderivative of a function like cosine theta, where the antiderivative is the corresponding sine function, and then evaluating it between the given limits.
Outlines
📚 Introduction to the Fundamental Theorem of Calculus
This paragraph introduces the Fundamental Theorem of Calculus, which is divided into two parts. Part one discusses the concept of antiderivatives and their relationship with definite integrals, explaining that the derivative of an antiderivative is equal to the original function. The explanation includes an example of finding the derivative of the integral of a function from 0 to x, showcasing how to apply the theorem in problem-solving. The paragraph emphasizes that integration and differentiation are inverse processes, and it provides a foundation for understanding calculus.
🔢 Applying the Fundamental Theorem of Calculus - Examples
This section delves into applying the Fundamental Theorem of Calculus through various examples. It explains how to find the derivative of integrals by replacing the variable of integration with the variable of differentiation. The paragraph covers different scenarios, such as when the upper and lower limits of integration are constants or variables, and how to handle these cases. It also touches on the concept of antiderivatives and their use in evaluating definite integrals, illustrating this with examples involving polynomial and trigonometric functions.
📈 Fundamental Theorem of Calculus Part Two - Explanation and Application
The paragraph focuses on the second part of the Fundamental Theorem of Calculus, which relates the definite integral of a continuous function on a closed interval to the antiderivative of that function. It explains that the integral of a function from a to b is equal to the antiderivative evaluated at b minus the antiderivative evaluated at a. The paragraph provides examples of applying this concept to find the area under a curve, demonstrating how to evaluate the antiderivative at specific points and calculate the difference.
🧮 Advanced Examples of Applying the Fundamental Theorem of Calculus
This paragraph presents more complex examples of applying the Fundamental Theorem of Calculus, involving functions with exponents and trigonometric functions. It shows how to find antiderivatives by manipulating the function's exponent and then evaluating the antiderivative at the given interval's endpoints. The examples include calculating integrals with variable limits and emphasize the importance of understanding the relationship between derivatives and antiderivatives in calculus.
🤝 Combining Parts One and Two of the Fundamental Theorem - Problem Solving
The paragraph combines the concepts from both parts of the Fundamental Theorem of Calculus to solve problems that involve finding the derivative of an integral. It explains that the antiderivative of a function can be evaluated between two points to find the definite integral, and the derivative of the integral can be found by applying the chain rule. The examples provided illustrate how to handle more complicated functions and emphasize the power of the theorem in solving calculus problems.
🌟 Wrapping Up and Additional Examples
In the final paragraph, the video wraps up by providing additional examples to reinforce the concepts learned. It demonstrates how to find the antiderivative of more complex functions, such as those involving natural logarithms and secants, and how to evaluate these antiderivatives at specific intervals. The paragraph also reiterates the process of finding the derivative of an integral by replacing the integration variable with the differentiation variable, and it encourages practice to master these techniques.
Mindmap
Keywords
💡Fundamental Theorem of Calculus
💡Antiderivivative
💡Derivative
💡Integration
💡Continuous Function
💡Definite Integral
💡Chain Rule
💡Differentiation
💡Integration by Substitution
💡Limits of Integration
Highlights
Introduction to the Fundamental Theorem of Calculus Part 1 and Part 2.
Explanation of g(x) as the antiderivative of a function from 'a' to 'x'.
Continuous functions and their implications on the differentiability of g(x).
Derivative of g(x) being equal to f(x), illustrating the inverse relationship between integration and differentiation.
Application of the Fundamental Theorem of Calculus in solving problems.
Example of finding the derivative of the integral from 0 to x of √(1 + 3t) dt.
Derivation of g'(x) = √(1 + 3x) using the Fundamental Theorem of Calculus.
Another example with g(x) as the antiderivative of ∫(4 to x) ln(t) dt.
Explanation of g'(x) = ln(x) using the Fundamental Theorem of Calculus.
Demonstration of replacing 't' with 'x' to find the derivative of an integral.
Introduction to the Fundamental Theorem of Calculus Part 2.
Use of capital F(x) to represent the antiderivative of f(x) and its application.
Illustration of calculating the integral from 1 to 3 of x^2 dx using Part 2 of the theorem.
Example of finding the antiderivative from 3 to 8 of (5x - 2) dx.
Explanation of the process for finding the antiderivative when the lower limit is different from the upper limit.
Demonstration of calculating the integral from 1 to 4 of √x dx using Part 2 of the theorem.
Example of calculating the integral from π/6 to π/3 of cos(θ) dθ.
Explanation of the antiderivative of secant squared and its evaluation from 0 to π/4.
Final example of finding the antiderivative from 1 to 2 of (5x * (2x - x^3)) dx.
Summary of the methods for finding derivatives of integrals using both fast approximation and step-by-step justification.
Transcripts
Browse More Related Video

Fundamental Theorem of Calculus Explained | Outlier.org
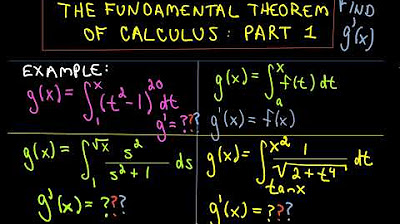
Fundamental Theorem of Calculus Part 1

Fundamental Theorem of Calculus Parts 1&2

Lec 20 | MIT 18.01 Single Variable Calculus, Fall 2007

Calculus (Version #2) - 9.1 The Second Fundamental Theorem of Calculus
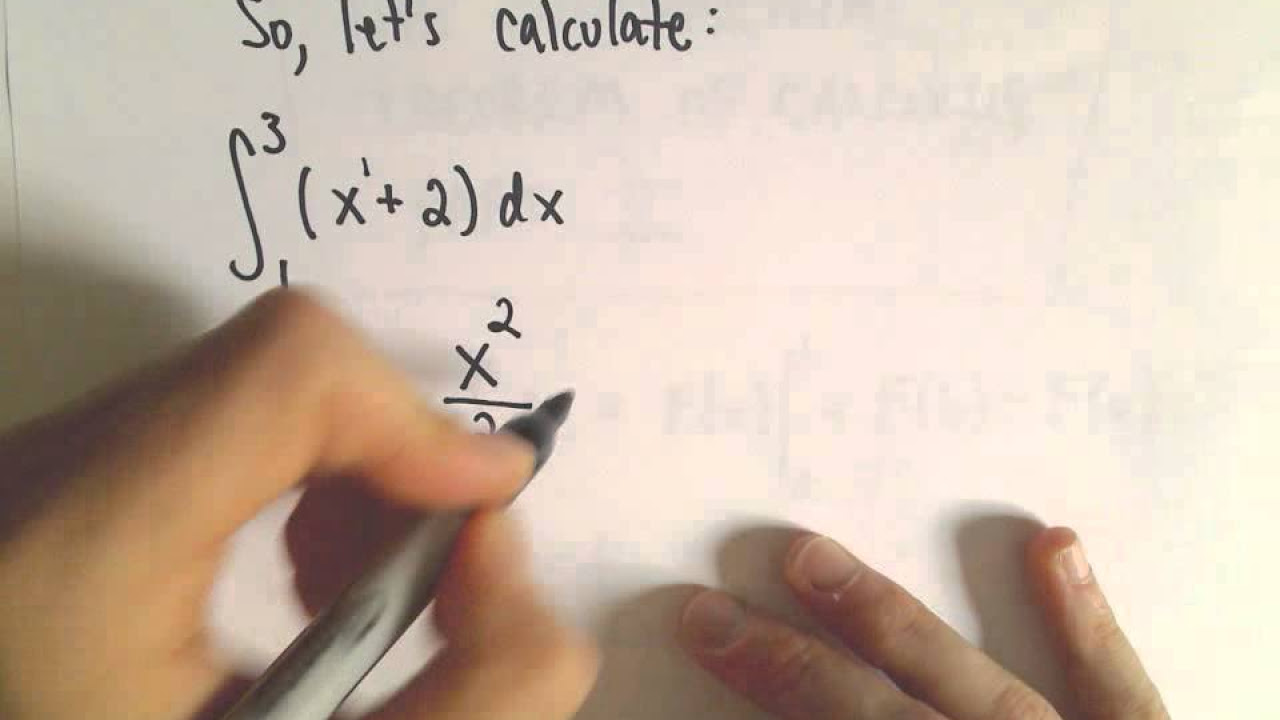
The Fundamental Theorem of Calculus. Part 2
5.0 / 5 (0 votes)
Thanks for rating: