Variance of sum and difference of random variables | Random variables | AP Statistics | Khan Academy
TLDRThis video script explores the concept of random variables, specifically the weight of a cereal box and a bowl filled with cereal, using 'Mathies' as an example. It explains the expected values and standard deviations for both variables, emphasizing the importance of independence in calculating the variance of their sum or difference. The script builds intuition about how the range and variability of these combined variables increase, concluding with the calculation of the standard deviation for the combined weight.
Takeaways
- 📊 The script introduces two random variables, X and Y, representing the weight of a cereal box and the weight of cereal in a bowl, respectively.
- 🔢 The expected value (mean) of X is given as 16 ounces, with a standard deviation of 0.8 ounces, indicating the average weight and the measure of variation for the cereal box.
- 📦 It is explained that the actual weight of cereal boxes can vary due to factors like flake density and packing, and the company discards boxes outside the 15 to 17 ounces range.
- 🥣 The expected weight of cereal in a bowl (Y) is four ounces with a standard deviation of 0.6 ounces, reflecting the variability in filling the bowl.
- 🚫 Bowls are also subject to quality control, with the weight of cereal in a bowl constrained between three and five ounces.
- ➕ The script discusses the concept of combining these two random variables, specifically focusing on the sum X + Y, and its expected value which is the sum of the individual expected values (20 ounces).
- 📊 The variance of the sum or difference of two independent random variables is equal to the sum of their variances, a key principle in probability theory.
- ❗️ It is emphasized that the standard deviation of the sum of two variables cannot be found by simply adding the standard deviations; instead, variances must be added.
- 🔍 The script builds intuition about the increased variability when combining random variables, as seen in the broader range of possible values for X + Y compared to individual variables.
- 🧠 The importance of independence between random variables X and Y for the principle of variance addition to hold is mentioned, with a promise of further explanation in a future video.
- 📐 The script concludes with a calculation of the standard deviation for the sum X + Y, which turns out to be 1 ounce, derived from the sum of the variances of X and Y.
Q & A
What is the expected value of the weight of a random box of Mathies cereal?
-The expected value of the weight of a random box of Mathies cereal is 16 ounces.
What does the standard deviation of 0.8 ounces for the random variable X represent?
-The standard deviation of 0.8 ounces represents the measure of variation in the weight of the cereal boxes from the expected value.
Why can't the standard deviations of two random variables be simply added together?
-The standard deviations of two random variables cannot be simply added together because the standard deviation measures the spread of a single variable, not the combined effect of two variables.
What is the relationship between the variance of X plus Y and the individual variances of X and Y?
-The variance of X plus Y is equal to the sum of the variances of X and Y, assuming X and Y are independent random variables.
What is the expected weight of Mathies cereal in a four-ounce bowl?
-The expected weight of Mathies cereal in a four-ounce bowl is four ounces.
What is the standard deviation of the weight of Mathies cereal in a bowl, and what does it measure?
-The standard deviation of the weight of Mathies cereal in a bowl is 0.6 ounces, which measures the variation in the weight of the cereal in the bowl from the expected value.
What are the constraints on the weight of a random box of Mathies cereal?
-The weight of a random box of Mathies cereal is constrained to be greater than or equal to 15 ounces and less than or equal to 17 ounces.
What is the maximum and minimum value that the random variable Y (bowl weight) can take on?
-The maximum value Y can take on is five ounces, and the minimum value is three ounces.
How is the expected value of the combined weight of a random box of Mathies cereal and a random filled bowl calculated?
-The expected value of the combined weight is calculated by adding the expected values of X (cereal weight) and Y (bowl weight), which is 16 ounces plus four ounces, resulting in 20 ounces.
What is the variance of the sum of two independent random variables X and Y?
-The variance of the sum of two independent random variables X and Y is equal to the sum of their individual variances, which is the variance of X plus the variance of Y.
What is the standard deviation of the sum of X and Y, given the standard deviations of X and Y are 0.8 and 0.6 ounces respectively?
-The standard deviation of the sum of X and Y is calculated by taking the square root of the sum of their variances. Given the variances are 0.64 (0.8 squared) and 0.36 (0.6 squared), the combined variance is 1, and thus the standard deviation is 1 ounce.
How does the range of the sum of two random variables compare to the range of each individual variable?
-The range of the sum of two random variables can be larger than the range of each individual variable, as the extremes of the sum can be further from the mean compared to the extremes of the individual variables.
Outlines
📊 Understanding Random Variables and Their Combinations
This paragraph introduces two random variables, X and Y, representing the weight of a cereal box and the weight of cereal in a bowl, respectively. It explains that while the expected value of X is 16 ounces, with a standard deviation of 0.8 ounces, there is a constraint that X must be between 15 and 17 ounces. Similarly, Y has an expected value of four ounces with a standard deviation of 0.6 ounces, constrained between three and five ounces. The paragraph then explores the concept of combining these variables, specifically focusing on the sum X + Y, and discusses the calculation of expected values and the misconception of adding standard deviations to find the standard deviation of the sum. It emphasizes that the correct approach is to add variances, assuming independence between X and Y, and provides an intuitive explanation of why the range and variability of the sum are larger than the individual variables.
🔍 Variance of Sums and Differences of Independent Variables
Building upon the previous discussion, this paragraph delves into the variance of the sum and difference of the two random variables, X and Y. It challenges the notion of subtracting variances to find the variance of X - Y, instead illustrating through examples that the variability increases with both sums and differences. The paragraph clarifies that the variance of X + Y or X - Y is the sum of the individual variances, given the independence of X and Y. It then calculates the standard deviation of X + Y by squaring the standard deviations of X and Y to find their variances, summing these to get the total variance, and finally taking the square root to arrive at a standard deviation of one. The summary concludes by reinforcing the concept that the variability of the combined variables increases, setting the stage for further exploration of the importance of independence in the next video.
Mindmap
Keywords
💡Random Variables
💡Expected Value
💡Standard Deviation
💡Variance
💡Independence
💡Range
💡Combination of Random Variables
💡Cereal Box
💡Bowl
💡Variability
Highlights
Introduction of two random variables, X and Y, representing the weight of cereal in a box and the weight in a bowl respectively.
X represents the weight of a random box of Mathies cereal with an expected value of 16 ounces.
The expected value of X is indicated on the cereal box, but it does not guarantee every box will weigh exactly 16 ounces due to variations.
Standard deviation of X is 0.8 ounces, indicating the measure of variation in the weight of the cereal boxes.
The weight of cereal boxes is constrained between 15 and 17 ounces due to quality control measures.
Y represents the expected weight of cereal in a four-ounce bowl with a standard deviation of 0.6 ounces.
Bowls with cereal are also constrained in weight, ranging from three to five ounces for quality control.
The combined weight of a random box of cereal and a filled bowl is represented by the sum X + Y.
The expected value of the sum X + Y is the sum of the expected values of X and Y, which equals 20 ounces.
Variance of the sum X + Y is the sum of the variances of X and Y, assuming independence of the variables.
The standard deviation cannot be simply added for the sum of random variables, but variances can be.
The range of the sum X + Y is wider, with a maximum of 22 ounces and a minimum of 18 ounces.
The variance of X - Y is also the sum of the variances of X and Y, assuming X and Y are independent.
Calculation of the standard deviation of X + Y results in a value of 1 ounce, derived from the sum of the variances.
The video builds intuition on why the variability increases when dealing with the sum or difference of independent random variables.
Upcoming video will delve into the importance of independence in the context of variance calculations for sums and differences of random variables.
Transcripts
Browse More Related Video

Elementary Statistics - Chapter 5 Probability Distributions Part 1
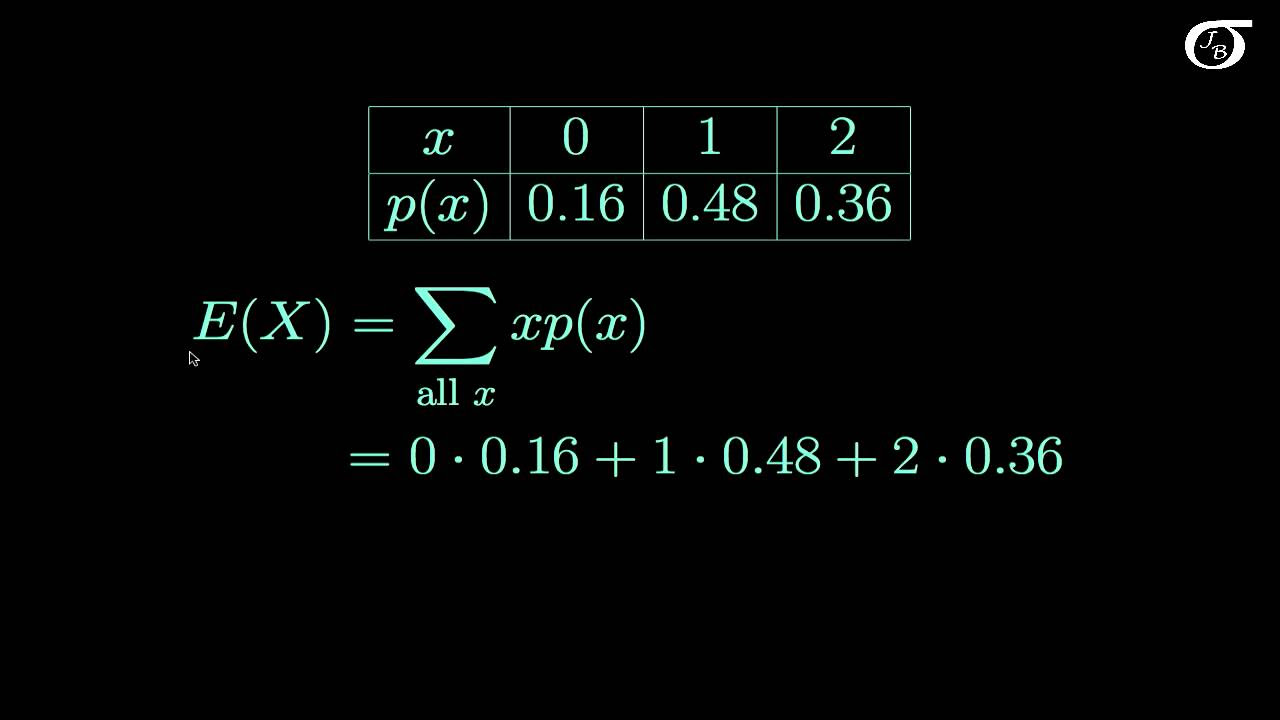
Expected Value and Variance of Discrete Random Variables
Lecture 14: Location, Scale, and LOTUS | Statistics 110

Elementary Stats Lesson #9

Measures of Dispersion (Ungrouped Data) | Basic Statistics

Understanding Standard deviation and other measures of spread in statistics
5.0 / 5 (0 votes)
Thanks for rating: