Equation for simple harmonic oscillators | Physics | Khan Academy

Khan Academy Physics
29 Jul 201614:13
EducationalLearning
32 Likes 10 Comments

TLDRThis instructional video explains the concept of simple harmonic motion using a horizontal position graph. It describes how amplitude and period are represented and how to derive the equation for such motion. The instructor guides through choosing between sine and cosine functions based on the starting point of the motion, adjusting amplitude, and calculating the angular frequency to match the period of oscillation. The final equation is presented as amplitude times cosine (or sine) of two pi over the period times time, offering a clear method to determine the position of a mass at any given moment in its oscillation.

Takeaways
  • πŸ“Š The motion of a simple harmonic oscillator can be represented on a horizontal position graph, typically in the shape of a sine or cosine wave.
  • πŸ” The amplitude of the motion is the maximum displacement from equilibrium and is depicted as the peak of the wave on the graph.
  • ⏱ The period (T) is the time it takes for the motion to complete one full cycle, which can be represented from peak to peak or any analogous point on the cycle.
  • πŸ“ By adjusting the amplitude and period, one can represent different oscillators using the same sine or cosine function, just by stretching the graph vertically or horizontally.
  • πŸ”’ The equation for the graph is a function that gives the position of the mass as a function of time, and it is crucial for describing the motion of the oscillator.
  • πŸŒ€ The choice between sine and cosine depends on the starting point of the motion; cosine is used if the motion starts at a maximum, while sine is used if it starts at zero or an equilibrium point.
  • πŸ”„ The amplitude of the oscillator is represented by a variable (A) in the equation, allowing the equation to describe oscillators with different maximum displacements.
  • πŸŽ› The angular frequency (Ο‰), derived from the period of the oscillator, is used in the equation to adjust the resetting point of the cosine function to match the period of the oscillator.
  • πŸ”„ The equation for the position of a simple harmonic oscillator as a function of time is generally in the form of Β±A * cos(2Ο€/T * t), where A is the amplitude, T is the period, and t is the time variable.
  • πŸ“š Understanding the unit circle and angular velocity concepts is essential for grasping how the function represents cyclic processes and resets according to the period.
  • πŸ“‰ The equation can be easily adjusted for different starting conditions of the oscillator, such as starting at a minimum or from equilibrium, by introducing a negative sign in front of the cosine function.
Q & A

  • What is a simple harmonic oscillator and how is its motion represented on a graph?

    -A simple harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force proportional to the displacement. Its motion is typically represented on a graph as a sinusoidal curve, either a sine or cosine function, which shows the position of the oscillator as a function of time.

  • What does the amplitude of a simple harmonic oscillator represent on the graph?

    -The amplitude represents the maximum displacement of the oscillator from its equilibrium position. It is depicted as the maximum value of the sinusoidal curve on the graph.

  • What is the period (T) of a simple harmonic oscillator and how is it shown on the graph?

    -The period (T) is the time it takes for the oscillator to complete one full cycle and return to its starting position. On the graph, it is shown as the time interval from peak to peak, trough to trough, or any point to its analogous point in the next cycle.

  • How can you adjust the amplitude and period of a simple harmonic oscillator on the graph?

    -You can adjust the amplitude by stretching the graph vertically, making the peak values larger or smaller without changing the period. To adjust the period, you stretch the graph horizontally, changing the time it takes to complete a cycle, while keeping the amplitude constant.

  • What is the mathematical equation used to describe the motion of a simple harmonic oscillator?

    -The mathematical equation is a function of time that describes the position of the oscillator. It is typically in the form of A * cos(Ο‰ * t + Ο†) or A * sin(Ο‰ * t + Ο†), where A is the amplitude, Ο‰ is the angular frequency, t is time, and Ο† is the phase angle.

  • Why might you choose cosine over sine to represent the motion of a simple harmonic oscillator starting at a maximum?

    -You would choose cosine over sine if the oscillator starts at a maximum displacement because the cosine function has a value of one at t=0, representing the maximum amplitude. Sine, on the other hand, starts at zero and increases to one.

  • What variable represents the amplitude in the equation of a simple harmonic oscillator?

    -The variable representing the amplitude in the equation is typically denoted by 'A'. It is the factor by which the cosine or sine function is multiplied to scale the motion to the correct amplitude.

  • What is the significance of the angular frequency (Ο‰) in the equation for a simple harmonic oscillator?

    -The angular frequency (Ο‰) determines how quickly the oscillator completes a cycle. It is used to adjust the period of the motion so that the function resets after the desired time interval, matching the oscillator's period.

  • How can you represent a simple harmonic oscillator with a different period using the same equation?

    -To represent an oscillator with a different period, you adjust the value of Ο‰ (angular frequency) in the equation. By changing Ο‰, you effectively change the period of the cosine or sine function without altering its amplitude.

  • What does the phase angle (Ο†) in the equation represent, and how does it affect the graph?

    -The phase angle (Ο†) represents the horizontal shift of the sinusoidal curve. A positive phase angle shifts the graph to the right, while a negative phase angle shifts it to the left, affecting the starting point of the oscillator's motion.

  • How do you determine whether to use a positive or negative cosine (or sine) in the equation based on the starting position of the oscillator?

    -You use a positive cosine if the oscillator starts at a maximum or minimum (depending on the direction of motion), and a negative cosine if it starts at the opposite extreme. Similarly, use a positive sine if the oscillator starts at equilibrium and moves upward, and a negative sine if it starts at equilibrium and moves downward.

Outlines
00:00
πŸ“š Introduction to Simple Harmonic Motion Graphs

The instructor begins by explaining how to represent the motion of a simple harmonic oscillator on a horizontal position graph, highlighting the amplitude as the maximum displacement from equilibrium and the period as the time for one complete cycle. The use of sine or cosine functions to represent any motion is introduced, with amplitude adjustments vertically and period adjustments horizontally. The need for an equation to describe the graph is emphasized, focusing on the position of the mass as a function of time, and the importance of selecting between sine and cosine based on the starting point of the motion.

05:01
πŸ” Developing the Equation for Simple Harmonic Oscillator Motion

The instructor delves into the process of deriving the equation for a simple harmonic oscillator. Starting with the cosine function due to its maximum value at zero, the amplitude is incorporated by multiplying the cosine by this value. The concept of angular velocity (omega) is introduced to adjust the period of the function to match the oscillator's period, rather than the default two pi seconds. The angular frequency is calculated as two pi over the period, and its role in resetting the function every cycle is explained. The instructor demonstrates how to apply this understanding to create a function that accurately represents the motion over any given time period.

10:01
πŸ“˜ Applying the Equation to Specific Oscillator Motions

The instructor illustrates how to apply the derived equation to describe the motion of a simple harmonic oscillator with a specific amplitude and period. Using the amplitude of 0.2 meters and a period of six seconds as an example, the function is constructed by plugging in these values. The importance of leaving the time variable as is to allow for dynamic calculations of position at any given moment is stressed. The instructor also addresses how to handle different starting positions on the graph by using positive or negative cosine and sine functions, and provides a general formula for the motion of a simple harmonic oscillator, encapsulating the amplitude, angular frequency, and time variable.

Mindmap
Keywords
πŸ’‘Simple Harmonic Oscillator
A simple harmonic oscillator (SHO) is a system that, when displaced from its equilibrium position, experiences a restoring force proportional to the displacement, often due to elastic or gravitational forces. In the video, the SHO represents the motion being discussed, and the instructor uses the concept to explain the periodic motion of an object, such as a mass attached to a spring.
πŸ’‘Amplitude
Amplitude refers to the maximum displacement of the oscillator from its equilibrium position. It is a measure of the extent of oscillation. In the script, amplitude is used to describe the vertical stretch of the motion graph, indicating how far the mass is displaced at its maximum.
πŸ’‘Period
The period (T) is the time taken for one complete cycle of the oscillation to occur. It is a fundamental property of periodic phenomena, including the motion of SHOs. The instructor explains that the period is the time from peak to peak or from any point to its analogous point in the next cycle of the SHO's motion.
πŸ’‘Sine and Cosine
Sine and cosine are trigonometric functions that describe the relationship between the angles and the sides of a right-angled triangle or the coordinates of points on the unit circle. In the context of the video, they are used to model the SHO's motion, with sine or cosine functions representing the position of the mass as a function of time.
πŸ’‘Equation of Motion
The equation of motion is a mathematical expression that describes the position of an object as a function of time. In the video, the instructor discusses how to derive the equation of motion for an SHO, which involves choosing between sine and cosine functions and incorporating amplitude and period into the equation.
πŸ’‘Angular Velocity
Angular velocity (omega) is a measure of the rate of change of an angle with respect to time, often used in physics to describe rotational motion. In the script, angular velocity is used to adjust the frequency of the SHO's oscillation, allowing the period of the cosine function to match that of the oscillator.
πŸ’‘Phase Shift
A phase shift in the context of oscillations refers to a displacement of the entire waveform in the time domain, which can be represented mathematically by adding or subtracting a phase constant. Although not explicitly mentioned, the concept is implicitly discussed when the instructor talks about starting the motion at different points on the cosine function.
πŸ’‘Unit Circle
The unit circle is a circle with a radius of one, centered at the origin of a coordinate system. It is used in the video to explain the concept of angular frequency and how it relates to the periodic nature of SHOs. The instructor uses the unit circle to illustrate how cyclic processes can be represented.
πŸ’‘Radian Measure
Radian measure is a way of expressing angles based on the length of the arc they intercept on a unit circle, where 2Ο€ radians equal one full rotation. The instructor mentions radians in the context of angular frequency, explaining that the period of the SHO's motion is related to the number of radians the system rotates through in one cycle.
πŸ’‘Function
In mathematics, a function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. In the video, the function represents the position of the SHO as a function of time, allowing one to calculate the position of the mass at any given moment.
πŸ’‘Graph
A graph is a visual representation of data, showing the relationship between two or more variables. In the context of the video, the graph represents the position of the SHO over time, with the instructor explaining how different parameters like amplitude and period affect the shape and characteristics of the graph.
Highlights

Representing the motion of a simple harmonic oscillator using a horizontal position graph.

Amplitude is represented by the maximum displacement from equilibrium on the graph.

The period (T) is the time for the entire process to reset, measured from peak to peak or any analogous point.

Using sine or cosine functions to represent any motion of an oscillator by adjusting amplitude and period.

Equation for a graph represents the horizontal position X as a function of time.

Choosing between sine and cosine based on the starting point of the oscillator's motion.

Using cosine for the starting point at a maximum due to its value being one at T equals zero.

Adjusting the amplitude in the equation to match the oscillator's maximum displacement.

The necessity of multiplying the cosine function by the amplitude to scale the graph correctly.

Introducing angular frequency (omega) to adjust the period of the oscillator's motion.

Calculating angular frequency as two pi over the period to match the oscillator's cycle duration.

Representing cyclic processes using the unit circle and angular velocity.

The function resets every period, ensuring the graph's consistency with the oscillator's motion.

Using the variable t as the time input for calculating the position of the mass at any given moment.

Creating the equation for a simple harmonic oscillator by combining amplitude, cosine, angular frequency, and time.

The ease of adjusting the equation for different amplitudes and periods for various oscillators.

Understanding the choice between positive and negative cosine or sine based on the starting conditions of the motion.

The general equation for representing the motion of a simple harmonic oscillator, incorporating amplitude, sine/cosine, angular frequency, and time.

Transcripts

Browse More Related Video

Simple Harmonic Motion in Trig (Precalculus - Trigonometry 35)

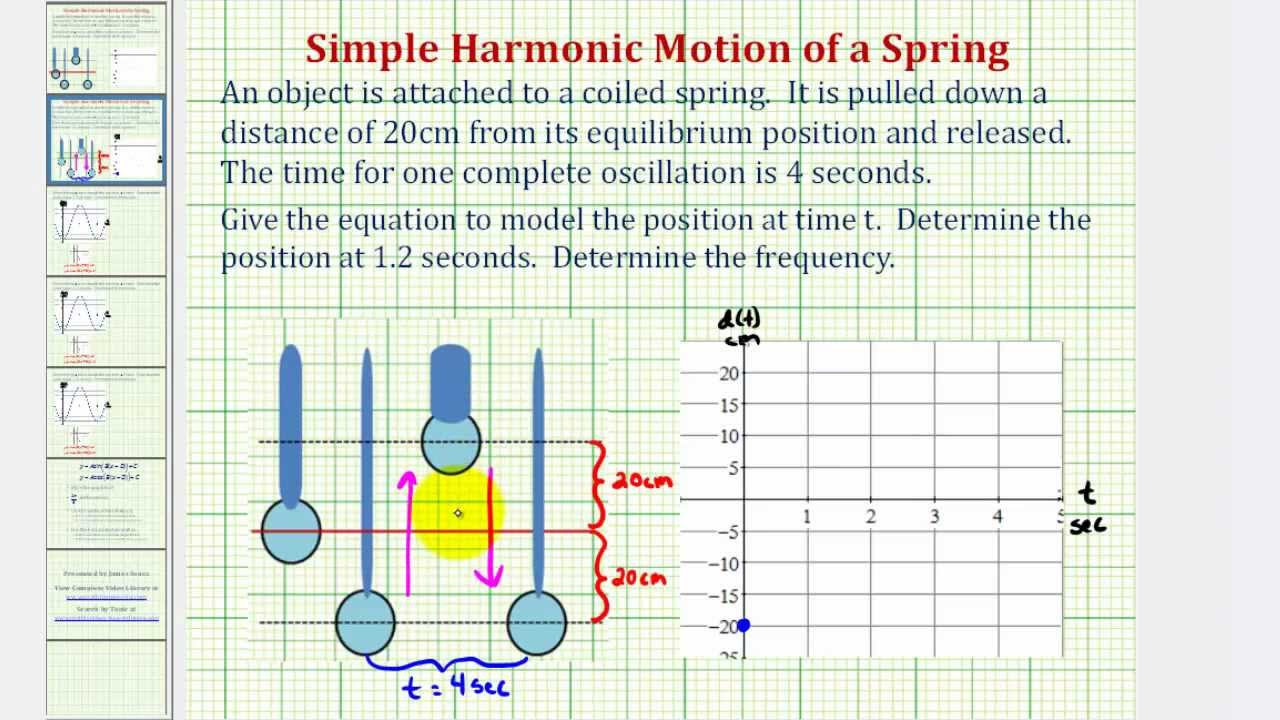
An Equation for Simple Harmonic Motion of a Spring

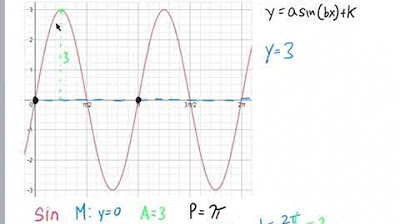
Writing Equations for Sinusoidal Functions

Simple Harmonic Motion - Complete Review of the Mass-Spring System

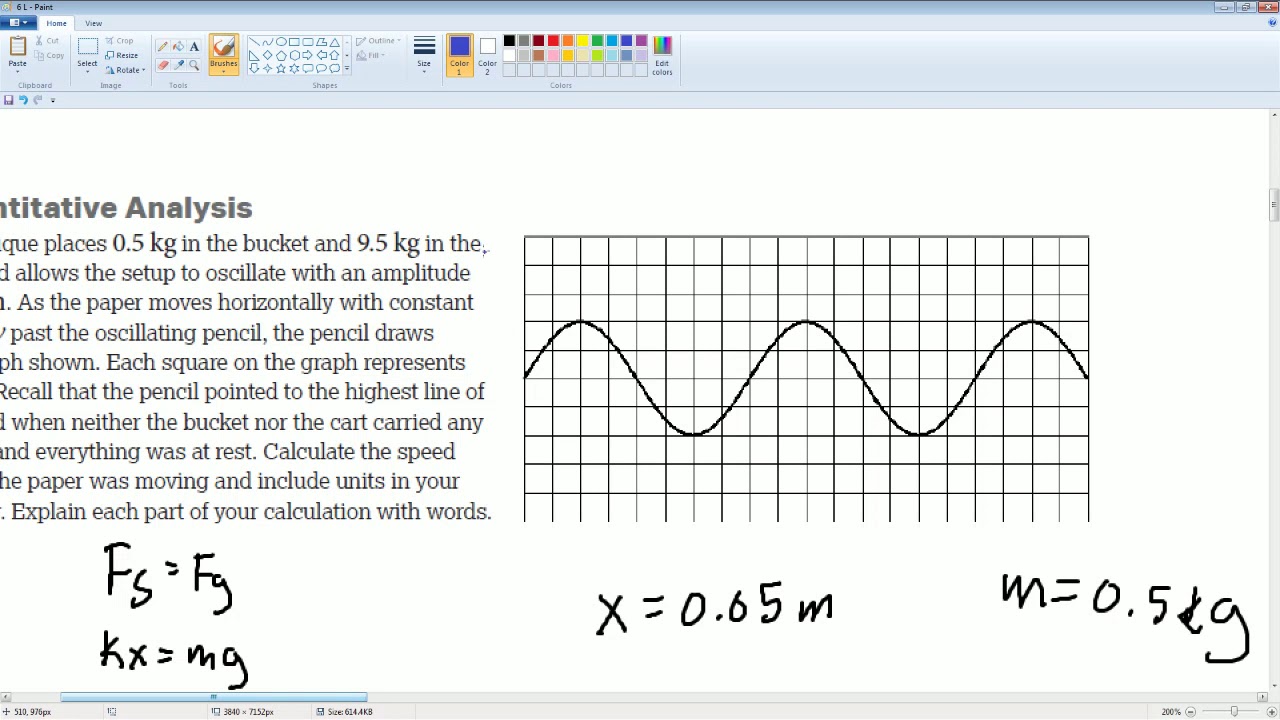
AP Physics Workbook 6.L Sine function of SHM

01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Simple HarmonicOscillator MotionAmplitudePeriodCosine FunctionTrigonometryPhysics TutorialWave AnalysisAngular FrequencyEducational ContentMotion Equation