Simple Harmonic Motion in Trig (Precalculus - Trigonometry 35)
TLDRThis video delves into the concept of simple harmonic motion, a type of oscillatory motion that persists without loss of energy over time. It contrasts this with damped harmonic motion, where the oscillation gradually decreases until it stops. The video explains how simple harmonic motion can be mathematically modeled using sine and cosine functions, emphasizing the importance of understanding the starting conditions of the motion to choose the correct function. The amplitude, period, and frequency of the motion are discussed, along with how to determine the initial direction of motion from the function's form. The script provides several examples to illustrate how to construct the displacement function for a given simple harmonic motion scenario, highlighting the key differences between using sine and cosine functions based on whether the motion starts at rest or from a displaced position. The video aims to give viewers a solid grasp of how to model and interpret simple harmonic motion mathematically.
Takeaways
- 📚 Simple harmonic motion is a type of oscillatory motion that does not decrease over time, meaning it continues indefinitely.
- 📈 The sine and cosine functions are used to model simple harmonic motion without any additional manipulations or bounding curves.
- 🔄 The amplitude of oscillation is the maximum distance from the resting position, and it's represented by the absolute value of 'a' in the function.
- ⏳ The period of oscillation, often denoted as 'T', is related to the angular frequency 'ω' by the formula T = 2π/ω.
- 🔢 The frequency of oscillation is the reciprocal of the period and represents the number of oscillations per unit time.
- 🔴 If the motion starts from a resting position, the sine function is used, as it starts at the origin (zero displacement).
- 🔵 If the motion starts away from the resting position, the cosine function is used, as it can represent an initial positive or negative displacement.
- 📉 For cosine functions, the initial motion is downward if the object is pushed or pulled away from rest and then released.
- 📈 For sine functions, the initial motion is upward if the object starts from rest and is then set in motion.
- 🧮 The vertical shift in a function does not affect the amplitude, which is solely determined by the coefficient of the sine or cosine term.
- ⏰ The displacement at time zero can be determined by plugging in 't=0' into the function, which helps to verify the initial conditions of the motion.
Q & A
What is simple harmonic motion?
-Simple harmonic motion is a type of vibratory motion that does not lessen over time. It refers to an oscillation where an object moves back and forth repeatedly around an equilibrium position at a constant amplitude and frequency.
How can simple harmonic motion be modeled mathematically?
-Simple harmonic motion can be modeled using sinusoidal functions, specifically sine or cosine functions. These functions describe the displacement of an object over time in a periodic manner without any change in amplitude.
What is the difference between using sine and cosine functions to model simple harmonic motion?
-The choice between sine and cosine functions depends on the initial position of the object. If the object starts its motion at rest, the sine function is used. If the object starts away from its resting position, the cosine function is used.
What is the amplitude in the context of simple harmonic motion?
-The amplitude in simple harmonic motion is the maximum distance that the object moves away from its equilibrium or resting position. It is represented by the absolute value of the coefficient 'a' in the sinusoidal function.
How is the period of simple harmonic motion determined?
-The period of simple harmonic motion is determined by the value of 'omega' (ω), which is the coefficient of the variable 't' in the sinusoidal function. The period is given by the formula (2π)/ω, which represents the time taken for one complete oscillation.
What is the relationship between the period and frequency of simple harmonic motion?
-The frequency of simple harmonic motion is the reciprocal of the period. It represents the number of oscillations that occur per unit time. If the period is given by T, then the frequency (f) is calculated as f = 1/T.
How do you determine the initial motion of an object in simple harmonic motion?
-The initial motion of an object in simple harmonic motion can be determined by the type of sinusoidal function used (sine or cosine) and the sign of the amplitude. For a sine function, if the object starts at rest, it will move upward if the amplitude is positive and downward if the amplitude is negative. For a cosine function, the object will move downward if the amplitude is positive and upward if the amplitude is negative, regardless of the starting position.
What is the significance of the vertical shift in a sinusoidal function representing simple harmonic motion?
-A vertical shift in a sinusoidal function represents a change in the equilibrium or resting position of the object undergoing simple harmonic motion. It does not affect the amplitude or the maximum displacement from the resting position but does change the starting position of the object.
How can you determine if a given motion is simple harmonic motion based on its mathematical model?
-A motion is considered simple harmonic if its mathematical model is a sinusoidal function (sine or cosine) without any exponential decay term, which would indicate damping. The function should exhibit periodic behavior with a constant amplitude and frequency.
What is the effect of the coefficient of the variable 't' in a sinusoidal function on the period of simple harmonic motion?
-The coefficient of the variable 't' in a sinusoidal function, often denoted as 'omega' (ω), directly affects the period of the motion. A larger omega value results in a shorter period, meaning the object completes its oscillation more quickly. Conversely, a smaller omega value leads to a longer period.
What is the physical interpretation of the frequency in simple harmonic motion?
-The frequency in simple harmonic motion is the number of complete oscillations or cycles that an object undergoes in a unit of time, typically measured in oscillations per second. It is a measure of how often the object passes through its equilibrium position in a given time period.
How does the direction of the initial motion relate to the choice of sine or cosine function in modeling simple harmonic motion?
-The direction of the initial motion is determined by whether the object starts at rest or away from rest and the direction of the applied force. If the object starts at rest and is pushed or pulled, a sine function is used for modeling, with the object moving upward for a positive amplitude and downward for a negative amplitude. If the object is already displaced and then released, a cosine function is used, with the object moving downward for a positive amplitude and upward for a negative amplitude.
Outlines
🔄 Introduction to Simple Harmonic Motion
This segment introduces the concept of simple harmonic motion (SHM), emphasizing its undampened, perpetual nature characterized by consistent oscillations such as in sine and cosine functions. The video clarifies SHM's mathematical modeling using sinusoidal functions, explaining key parameters like displacement, amplitude, and period. It distinguishes between starting conditions using sine or cosine based on the initial position relative to the rest position. The example used involves pulling a sign attached to a spring to demonstrate these concepts practically.
🔍 Building Functions for SHM
This part of the script delves into creating specific functions for SHM by examining a scenario where a sign is pulled down and released. The focus is on calculating the amplitude, period, and frequency of the oscillation, with detailed steps on deriving these parameters from given conditions. The example explains using cosine to model the motion, showing how the function is built based on the initial displacement and period, and leading into a practical understanding of how to apply these concepts to predict and describe motion in real-time.
📈 Advanced SHM Functions and Applications
Continuing from previous examples, this section discusses different scenarios of SHM involving various initial conditions and displacements. It explains the selection of sine versus cosine functions based on whether the motion starts at rest or away from it. The segment covers how to manipulate the SHM formula to suit different starting conditions and how this affects the motion's trajectory. Practical examples include manipulating objects attached to springs and the resulting motion, emphasizing the mathematical principles governing these phenomena.
🤔 Analysis of SHM Through Different Functions
This paragraph explores SHM through the analysis of different sine and cosine functions. The discussion includes detailed explanations of how different coefficients and periods affect the motion's properties, such as amplitude and frequency. The script provides a walkthrough of checking these properties by plugging values into the functions, ensuring a correct understanding of how initial conditions influence the overall motion pattern. It stresses the importance of the function's form (positive or negative, sine or cosine) in determining the initial direction of the motion.
🌐 Exploring Sine and Cosine Functions in SHM
Here, the script breaks down the characteristics of a simple harmonic motion modeled by a sine function. It covers how to determine the amplitude, period, frequency, and initial conditions based on the function's parameters. The importance of understanding the starting position (at rest or in motion) and how this impacts the initial movement direction is highlighted. Real-life applications, like setting parameters for oscillatory systems, are discussed to illustrate the practical utility of understanding these mathematical models.
📏 Comprehensive Analysis of SHM Functions
The focus of this section is a comprehensive analysis of various SHM functions, providing detailed calculations for properties such as displacement, amplitude, period, and frequency. The script explains both sine and cosine functions, demonstrating how to derive these values from the mathematical formulae. This includes discussing the significance of initial conditions and how they affect the system's motion, offering a deep dive into the mechanics of simple harmonic motion in practical settings.
🎓 Concluding Insights on SHM Modeling
This final part offers a wrap-up of the key points discussed in the video regarding simple harmonic motion. It reinforces the concepts of sine and cosine functions as tools for modeling SHM, emphasizing the importance of initial conditions and their effects on motion. The discussion is geared towards ensuring a solid understanding of how to apply these concepts in theoretical and practical scenarios, providing viewers with the tools to analyze and predict the behavior of simple harmonic systems.
Mindmap
Keywords
💡Simple Harmonic Motion
💡Sine and Cosine Functions
💡Displacement
💡Amplitude
💡Period
💡Frequency
💡Angular Frequency (ω)
💡Damped Harmonic Motion
💡Initial Motion
💡Vertical Shift
💡Oscillation
Highlights
Simple harmonic motion is a type of vibratory motion that does not lessen over time.
Simple harmonic motion can be modeled using sinusoidal functions like sine and cosine without additional manipulations.
Displacement (d) in simple harmonic motion represents the distance between the resting position and the current position of the object.
The amplitude (a) is the maximum distance the object moves away from its resting position, indicating the extent of the vibration.
The angular frequency (ω) is related to the period of the motion and is a key factor in determining the oscillation speed.
The period (T) of simple harmonic motion is the time taken for one complete oscillation, and it's often related to 2π in the context of sine and cosine functions.
Frequency (f) is the number of oscillations per unit time and is the reciprocal of the period.
When starting from a non-resting position, the cosine function is used to model simple harmonic motion, while the sine function is used when starting from rest.
The choice between sine and cosine functions depends on whether the motion starts above or below the resting position.
A negative cosine function indicates a starting position below the resting position, while a positive cosine function starts above the resting position.
The initial motion of a simple harmonic system is upwards for a negative cosine function and downwards for a positive cosine function.
The initial motion of a sine function is upwards for a positive function and downwards for a negative function, always starting from the resting position.
The vertical shift in a function, like adding 6 to the cosine function, changes the resting position of the motion but not the amplitude.
The maximum displacement from rest is determined by the amplitude of the function, regardless of any vertical shifts.
Understanding the interplay between sine and cosine functions is crucial for accurately modeling and analyzing simple harmonic motion scenarios.
The initial motion and displacement from rest can be deduced from the choice of sine or cosine function and the sign of the amplitude.
Transcripts
Browse More Related Video

Equation for simple harmonic oscillators | Physics | Khan Academy
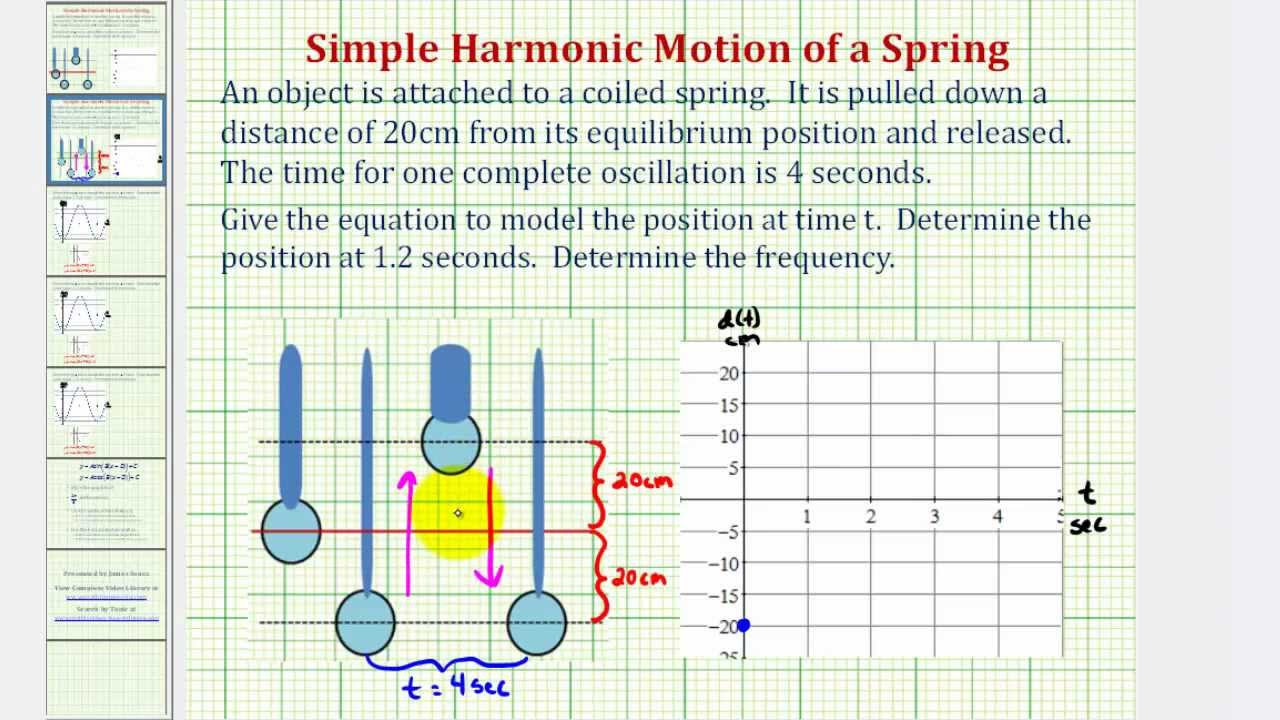
An Equation for Simple Harmonic Motion of a Spring
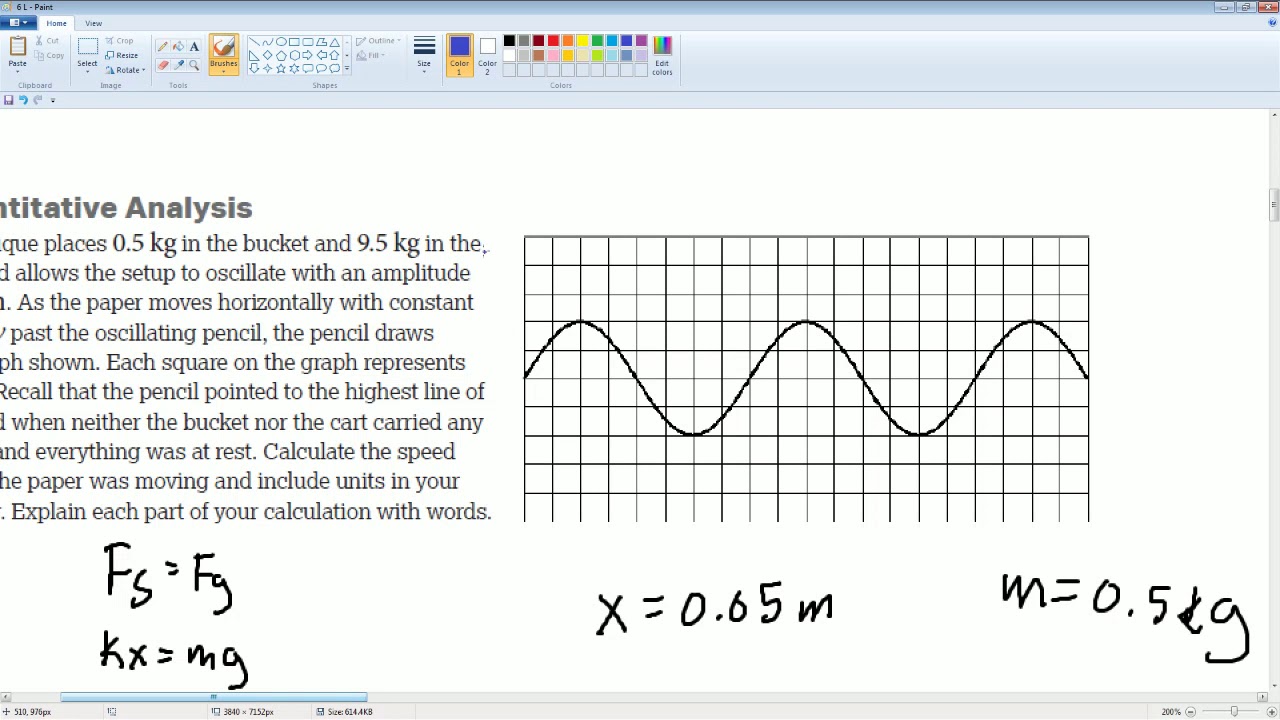
AP Physics Workbook 6.L Sine function of SHM

01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)
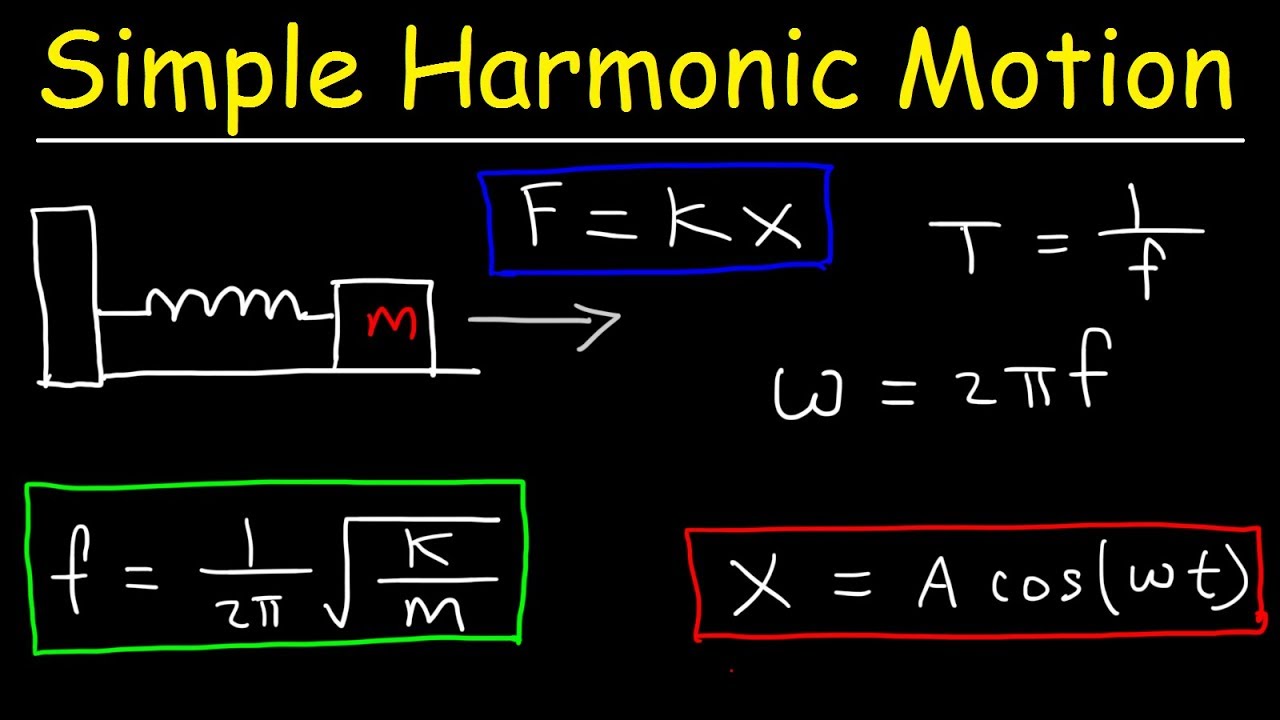
How To Solve Simple Harmonic Motion Problems In Physics

Simple Harmonic Motion: Crash Course Physics #16
5.0 / 5 (0 votes)
Thanks for rating: