2. Resonance II

The script begins with an introduction to the harmonic oscillator, a complex system in physics, emphasizing the importance of frequency measurement in precision physics. It mentions the accuracy of measurements done through frequency and introduces Fourier's theorem, which relates the time of oscillation to the spread of frequency components. The professor also discusses the relationship between Fourier's limit and Heisenberg's uncertainty principle, highlighting the relevance of these concepts to all precision measurements. The script then poses a question about the uncertainty in frequency measurement for classical systems, suggesting that a good signal-to-noise ratio could potentially allow for more precise measurements.

This paragraph delves into the impact of noise on wave-formed signals and the precision of frequency measurements. It explains that while Fourier's theorem sets a limit on the width of spectral components based on observation time, the center of the spectral peak can be determined more accurately, depending on the signal-to-noise ratio. The summary outlines the concept of 'splitting the line' to achieve greater measurement accuracy and touches on the challenges of ensuring the line shape is known and symmetric to accurately determine the frequency. The discussion also introduces the idea of measuring the frequency of a quantum-mechanical oscillator and an optical laser pulse, questioning whether the Heisenberg limit can be surpassed.

The script explores whether the frequency of a quantum-mechanical harmonic oscillator or an optical laser pulse can be measured with accuracy beyond the Heisenberg limit. It clarifies that a laser, despite being quantum in nature, can behave classically under certain conditions. The professor discusses the use of a strong local oscillator to create a beat note with a laser, which can be measured with high precision, suggesting that the signal-to-noise ratio can be significantly improved to enhance measurement accuracy. The paragraph also addresses the subtleties of the Heisenberg uncertainty principle and its application to single quantum systems versus multiple measurements or photons.

This section discusses the possibility of surpassing the Heisenberg limit in frequency measurement for quantum harmonic oscillators and the impact of using multiple photons. It explains that with n uncorrelated photons, the signal-to-noise ratio improves, allowing for better frequency resolution. The script also touches on the concept of the Heisenberg limit in the context of correlated photons and the potential for even higher precision measurements. The audience's confusion about the applicability of the uncertainty relation in different scenarios is addressed, highlighting the importance of signal-to-noise ratio in achieving higher accuracy.

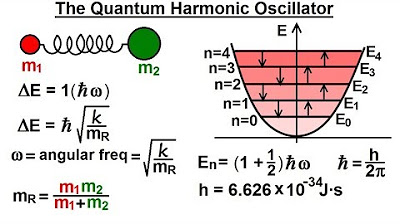
The script examines the analogy and differences between two-level systems and harmonic oscillators. It explains that a two-level system can be considered a harmonic oscillator under conditions of weak excitation, where only a small fraction of the system is in the first excited state. The concept of saturation is introduced as a distinguishing feature, where a two-level system can be saturated while a harmonic oscillator cannot. The script also discusses the Lorentz model for an atom, which illustrates the equivalence of a two-level system and a harmonic oscillator in certain conditions, and the phenomenon of saturation that distinguishes them.

This paragraph discusses the creation of non-classical states in cavity quantum electrodynamics (QED). It explains the challenge of selectively exciting the n=1 state in a harmonic oscillator and the use of anharmonicities or nonlinearities to achieve this. The script describes how the interaction between an atom and photons in a cavity can lead to normal mode splitting, which is proportional to the Rabi frequency, allowing for the creation of non-classical states of the photon field. The discussion highlights the difference between a pure harmonic oscillator and a system with an atom that can help overcome the limitations of the harmonic oscillator in preparing certain states.

The script introduces the concept of classical rotation, specifically focusing on the dynamics of magnetic moments in a magnetic field. It discusses the properties of a gyroscope and how the amplitude of its excitation is limited, drawing parallels with a two-level system. The professor emphasizes that the motion of classical magnetic moments can serve as an exact model for the dynamics of a quantum mechanical two-level system, highlighting the surprising similarities in their behavior. The limitations of this analogy, such as the absence of spontaneous emission in certain quantum systems, are also touched upon.

This section delves into the dynamics of a classical magnetic moment in magnetic fields, including both static and time-varying fields. The script explains the interaction energy between a classical magnetic moment and a magnetic field, the torque involved, and the resulting precession of angular momentum. The concept of the gyromagnetic ratio is introduced, which relates the magnetic moment to its angular momentum. The Larmor frequency, the frequency of precession, is also discussed, with examples provided for an electron, a classical charge distribution, and a proton.

The script explores the precession frequency of classical charge distributions and contrasts it with quantum mechanical systems, specifically focusing on the electron. It explains the difference in precession frequency due to the gyromagnetic ratio and the G factor of the electron. The importance of factors of 2 in understanding magnetic moments and precession systems is highlighted, using simple examples to illustrate the concepts. The script also discusses the relationship between the precession frequency and the energy levels of the system.

This paragraph discusses the method of solving the dynamics of a rotating system by transforming into a rotating frame of reference. The script explains the operator equation that relates the time derivative in the rotating frame to that in the inertial frame. It then applies this concept to the angular momentum of a precessing classical magnetic moment, showing how the equation of motion is modified in the rotating frame. The script also touches on the conditions under which the effective magnetic field vanishes, leading to a constant angular momentum in the rotating frame.

The script concludes with a discussion on the Larmor frequency and its relation to the cyclotron motion of electrons. It clarifies the difference between the Larmor frequency and the cyclotron frequency, highlighting the factor of 2 that separates them. The importance of understanding this distinction is emphasized, as it is crucial for comprehending the physics of magnetic moments and charged particles in magnetic fields. The script also references Larmor's theorem and its application to charge distributions, noting the differences between the exact dynamics of a magnetic moment and the approximated dynamics of a charge distribution.