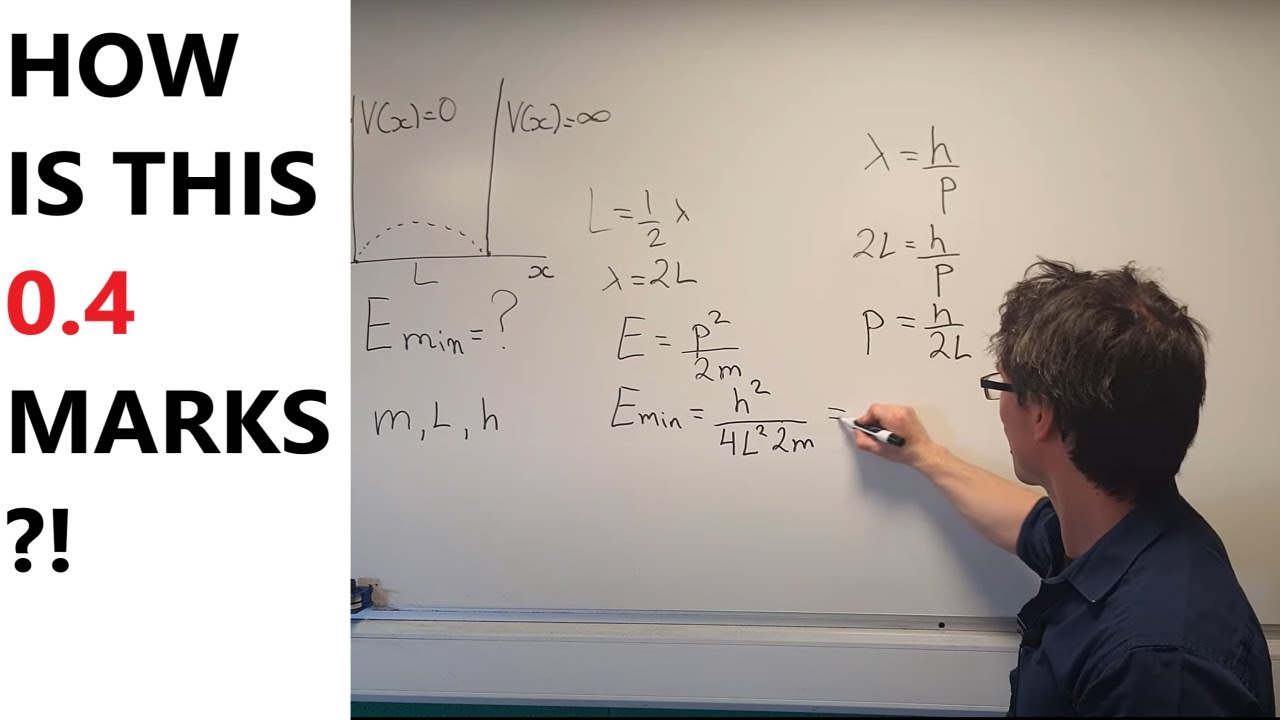Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (41 of 92) What is Zero Point Vibration?
TLDRThe transcript delves into the fascinating concept of zero-point vibration in quantum mechanics, which challenges classical assumptions by revealing that even at absolute zero temperature, particles exhibit vibrational motion. This phenomenon is explained through the Heisenberg uncertainty principle, which introduces a fundamental minimum energy level for quantum harmonic oscillators. The summary encapsulates the essence of quantum mechanics' ability to defy classical expectations, highlighting the strange and counterintuitive nature of the quantum world.
Takeaways
- 🌡️ At absolute zero temperature, classical mechanics suggests no vibrational motion, but quantum mechanics reveals the existence of zero-point vibration.
- 📐 The lowest possible energy level of a quantum harmonic oscillator is not zero due to the Heisenberg uncertainty principle.
- 🎵 Zero-point energy is given by E₀ = (1/2)ħω, where ħ is Planck's constant divided by 2π and ω is the angular frequency.
- 🔄 The Heisenberg uncertainty principle states that the product of the uncertainties in position and momentum is greater than or equal to ħ/2.
- 📈 The minimum energy of an oscillator is derived from the uncertainty principle, which prevents it from reaching zero energy.
- 🤔 Quantum mechanics challenges the classical view that particles can be precisely localized and have zero motion at absolute zero.
- 🌌 Zero-point vibration is a fundamental concept in quantum mechanics, showing that particles can exist in states that classical physics cannot explain.
- 🛠️ The general equation of an oscillator relates energy to the sum of kinetic and potential energies within the system.
- 🔢 By applying the Heisenberg uncertainty principle to the energy-momentum relationship, we can calculate the minimum energy state of an oscillator.
- 📊 The minimum energy is found by taking the derivative of the energy equation with respect to position uncertainty and setting it to zero.
- 🚧 The uncertainty principle allows for particles to be in places they 'shouldn't' be, such as inside barriers, and for energy to exist at absolute zero.
Q & A
What is zero-point vibration?
-Zero-point vibration is the concept in quantum mechanics that even at absolute zero temperature, there is still some residual vibrational motion in a quantum harmonic oscillator.
Why is there still motion at absolute zero in the quantum world?
-In the quantum world, the Heisenberg uncertainty principle dictates that there is always some uncertainty in the position and momentum of particles, which results in non-zero vibration even at absolute zero.
What is the lowest possible energy level of a quantum harmonic oscillator?
-The lowest possible energy level, denoted as E_0, is equal to (1/2)ħω, where ħ is Planck's constant divided by 2π and ω is the angular frequency of the oscillator.
How is the energy of an oscillator related to its kinetic and potential energy?
-The energy of an oscillator is the sum of its kinetic energy (1/2)mv^2 and its potential energy (1/2)kx^2, where m is the mass, v is the velocity, k is the spring constant, and x is the displacement from equilibrium.
What does the Heisenberg uncertainty principle state?
-The Heisenberg uncertainty principle states that the product of the uncertainties in position (Δx) and momentum (Δp) is greater than or equal to ħ/2, i.e., Δx * Δp ≥ ħ/2.
How does the uncertainty principle lead to the existence of zero-point energy?
-The uncertainty principle implies that particles cannot have perfectly defined positions and momenta simultaneously. This inherent uncertainty allows for the possibility of minimum non-zero energy states, such as zero-point energy.
What happens when we apply the uncertainty principle to the energy of an oscillator?
-By applying the uncertainty principle to the energy of an oscillator, we find that the minimum energy state cannot be zero due to the fundamental limits on our knowledge of position and momentum, leading to the concept of zero-point energy.
How does the angular frequency (ω) relate to the mass (m) and spring constant (k) of an oscillator?
-The angular frequency (ω) of an oscillator is given by ω = sqrt(k/m), where k is the spring constant and m is the mass of the oscillator.
What is the significance of zero-point energy in quantum mechanics?
-Zero-point energy is significant because it demonstrates the fundamental differences between classical and quantum mechanics, showing that quantum systems can never have zero energy due to the inherent uncertainty in their properties.
How does the concept of zero-point vibration challenge classical mechanics?
-Classical mechanics predicts that at absolute zero, all motion would cease. However, zero-point vibration shows that even at absolute zero, quantum systems exhibit residual motion, challenging this classical prediction.
What is the role of Planck's constant in the equation for zero-point energy?
-Planck's constant (ħ) is a fundamental constant in quantum mechanics, and it appears in the equation for zero-point energy (E_0 = (1/2)ħω) as a measure of the quantum scale, indicating the quantum nature of the energy.
Outlines
🌟 Quantum Mechanics and Zero-Point Vibrations
This paragraph introduces the concept of zero-point vibration in quantum mechanics, which challenges the classical assumption that at absolute zero temperature, there would be no vibrational motion. It explains that even at absolute zero, quantum harmonic oscillators possess a minimum energy level, represented as E₀ = (1/2)ħω. The Heisenberg uncertainty principle is key to understanding this phenomenon, as it implies that there is always some uncertainty in both position and momentum, leading to the existence of zero-point energy. The paragraph also delves into the mathematical derivation of the minimum energy an oscillator can have, emphasizing the relationship between kinetic and potential energy, and how the uncertainty principle influences the minimum energy state.
🌐 Implications of the Heisenberg Uncertainty Principle
The second paragraph elaborates on the implications of the Heisenberg uncertainty principle on the energy state of a quantum harmonic oscillator. It highlights that the minimum energy level, which is not zero, is a direct result of the inherent uncertainty in quantum mechanics. The paragraph explains that if the exact position and momentum of a particle were known at all times, the energy would theoretically reach zero. However, due to the uncertainty principle, this is impossible at the quantum level, leading to the existence of a non-zero minimum energy state. This principle also allows for phenomena such as particles tunneling through barriers and energy existing at absolute zero, which are fundamental aspects of quantum mechanics.
Mindmap
Keywords
💡Zero-point vibration
💡Quantum mechanics
💡Heisenberg uncertainty principle
💡Energy levels
💡Simple harmonic oscillator
💡Quantum harmonic oscillator
💡Planck's constant
💡Absolute zero
💡Momentum
💡Angular frequency
💡Uncertainty principle
Highlights
The concept of zero-point vibration in quantum mechanics is introduced, challenging classical mechanics' assumption of no motion at absolute zero.
In the quantum world, even at absolute zero temperature, there is still zero-point vibration, a fundamental principle of quantum mechanics.
The lowest possible energy level of a quantum harmonic oscillator is derived, represented as E sub 0.
Planck's constant (H bar) and its relation to the minimum energy level are explained within the context of quantum harmonic oscillators.
The Heisenberg uncertainty principle is key to understanding zero-point energy, linking the uncertainty in position and momentum.
The general equation of an oscillator is provided, relating energy to kinetic and potential components.
The relationship between momentum, velocity, and mass is used to express the kinetic energy of an oscillator in terms of momentum.
The angular frequency (Omega) is defined in terms of the spring constant (K) and mass (M), simplifying the energy equation.
The minimum energy of an oscillator is determined by the uncertainty principle, which introduces a nonzero lower energy limit.
The derivation of the minimum energy involves setting the derivative equal to zero and solving for the uncertainty in position.
The minimum energy expression is simplified to H bar Omega divided by 2, which is the energy of the first quantum state.
Quantum mechanics allows for particles to exist in states that classical mechanics would deem impossible, such as inside barriers or with nonzero energy at absolute zero.
The uncertainty principle has practical implications, affecting the behavior of particles and energy states at the quantum level.
The zero-point energy is a direct result of the inherent uncertainty in quantum mechanics, which cannot be eliminated even at absolute zero.
The transcript provides a detailed explanation of how the Heisenberg uncertainty principle leads to the existence of zero-point energy.
The minimum energy of an oscillator is not zero due to the fundamental principles of quantum mechanics and the uncertainty principle.
The example of zero-point vibration serves as a clear demonstration of the counterintuitive nature of quantum mechanics and its departure from classical theories.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: