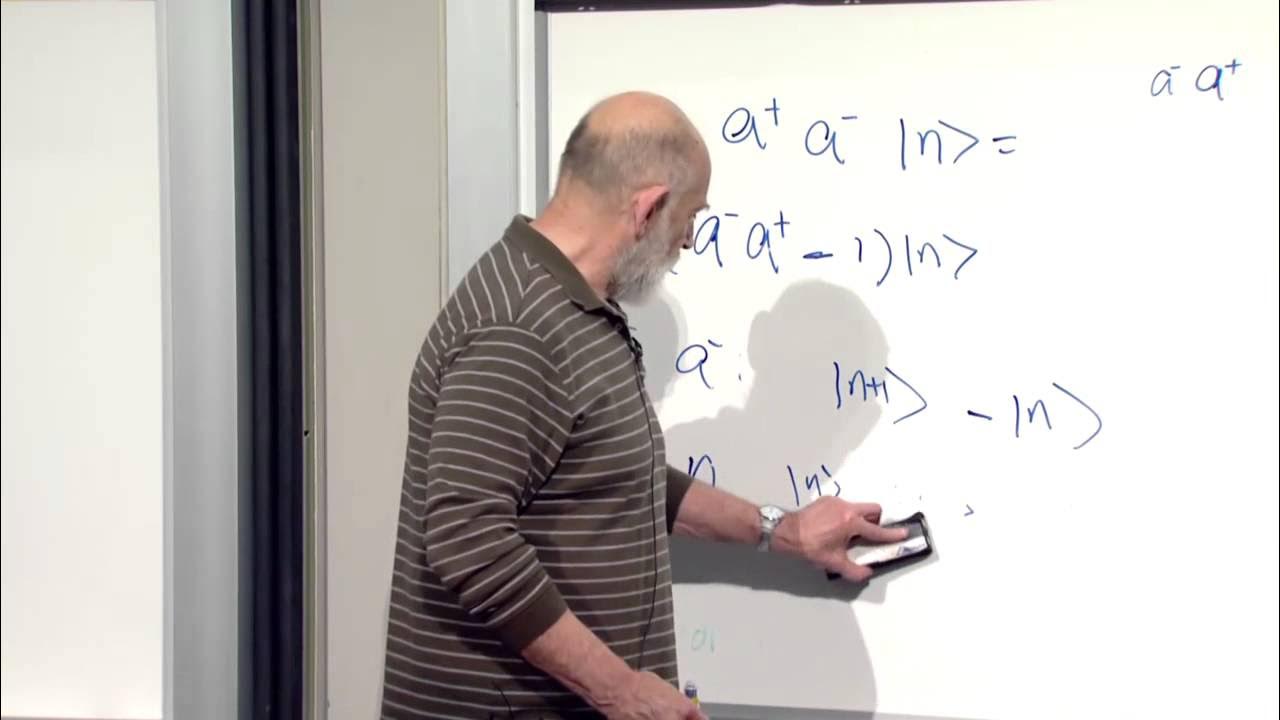Advanced Quantum Mechanics Lecture 4
TLDRThe video script is an in-depth exploration of the harmonic oscillator, a fundamental concept in physics that describes systems with an equilibrium state, such as a vibrating violin string or electromagnetic fields in a cavity. The lecturer delves into the quantum mechanical treatment of these systems, introducing creation and annihilation operators, and discusses the quantization of energy levels, highlighting the significance of the ground state energy or zero-point energy. The script also touches on the role of harmonic oscillators in quantum electrodynamics and the concept of sound waves as oscillations. Furthermore, the lecturer expands on the Hamiltonian formulation, the Heisenberg uncertainty principle, and the commutation relations. The discussion then transitions into the topic of spin, a form of angular momentum intrinsic to particles like electrons and protons, and the historical context that led to its discovery. The Pauli Exclusion Principle, which states that no two electrons can occupy the same quantum state simultaneously, is also explained. The script concludes with an introduction to the concepts of bosons and fermions, the two types of particles defined by their adherence to the exclusion principle, and their fundamental differences.
Takeaways
- 📚 The harmonic oscillator is a fundamental concept in physics, appearing in classical and quantum mechanics, and is used to describe systems that oscillate about an equilibrium state.
- 🎶 When a system with an equilibrium state is displaced, it tends to oscillate, possibly at multiple frequencies, as seen in examples like a violin string.
- 🌐 The electromagnetic field's equilibrium configuration is the vacuum state with no oscillations, and any disturbance can lead to oscillations described by photons.
- 🚀 Creation and annihilation operators, denoted as A+ and A-, are used in quantum mechanics to describe the behavior of harmonic oscillators and are related to the raising and lowering of energy levels.
- ⚛️ The Hamiltonian for a harmonic oscillator is derived from the creation and annihilation operators, and it includes a term known as the ground state energy or zero-point energy, which is a consequence of the uncertainty principle.
- 🌱 The ground state wave function of a simple harmonic oscillator is a Gaussian function, concentrated near the origin, and is indicative of the system's lowest energy state.
- ⏫ The first excited state wave function is an odd function, with a node at the origin, indicating that there is a zero probability of finding the oscillator at the origin in this state.
- 🔍 As the energy level (n) increases, the wave function of the harmonic oscillator develops more nodes and is pushed out further, reflecting higher potential and kinetic energy.
- 🤔 The correspondence principle suggests that for large quantum numbers, the behavior of quantum systems should resemble classical systems, which can be demonstrated through wave packets.
- 🧲 The concept of spin arose from the need to explain the periodic table and spectroscopic data, and it represents an intrinsic form of angular momentum.
- 📊 The spin of particles like electrons, protons, and neutrons is described by the Pauli matrices, which satisfy commutation relations similar to those of angular momentum, and has values of ±1/2.
Q & A
What is a harmonic oscillator?
-A harmonic oscillator is a system that experiences a restoring force proportional to the displacement from an equilibrium position, which often results in oscillatory behavior. It is a fundamental concept in physics that describes systems such as springs, pendulums, and even atoms or molecules.
Why are harmonic oscillators important in physics?
-Harmonic oscillators are important because they are ubiquitous in physics. They are used to describe a wide range of phenomena, from the vibrations of atoms and molecules to the oscillations of electromagnetic fields. They also form the basis for understanding more complex systems.
What is the significance of the ground state energy in a quantum harmonic oscillator?
-The ground state energy, also known as the zero-point energy, is significant because it represents the lowest possible energy level of a quantum harmonic oscillator. According to the Heisenberg uncertainty principle, a system cannot have zero energy, hence the ground state energy is always a positive, non-zero value.
How do creation and annihilation operators relate to the harmonic oscillator?
-Creation (a+) and annihilation (a-) operators are used in quantum mechanics to describe the quantum states of a harmonic oscillator. They allow for the raising and lowering of energy levels, and when combined, they can be used to construct the Hamiltonian for the system.
What is the role of the commutation relation in the context of harmonic oscillators?
-The commutation relation between the creation and annihilation operators is crucial as it ensures the quantization of the energy levels of the harmonic oscillator. It also reflects the uncertainty principle in quantum mechanics.
What is the correspondence principle in the context of the harmonic oscillator?
-The correspondence principle states that the behavior of a quantum system should approximate classical behavior in the limit of large quantum numbers. For a harmonic oscillator, this means that at high energy levels, the system's wave function dynamics should resemble those of a classical oscillator.
What does the term 'spin' refer to in quantum mechanics?
-In quantum mechanics, 'spin' refers to a fundamental property of particles, which is a type of intrinsic angular momentum. It is one of the two types of angular momenta, the other being orbital angular momentum, which arises from the motion of the particle in space.
What is the Pauli Exclusion Principle?
-The Pauli Exclusion Principle states that no two electrons in an atom can have the same set of quantum numbers. In other words, two identical fermions, such as electrons, cannot occupy the same quantum state simultaneously.
What are bosons and fermions?
-Bosons and fermions are two types of particles classified based on their spin. Bosons have integer spin and can occupy the same quantum state, while fermions have half-integer spin and follow the Pauli Exclusion Principle, meaning they cannot share the same quantum state.
How does the spin of an electron affect the energy levels of an atom?
-The spin of an electron, along with its orbital angular momentum, contributes to the total angular momentum of the atom. This total angular momentum determines the magnetic quantum number, which affects the energy levels of the atom, especially in the presence of a magnetic field, leading to the Zeeman effect.
What is the significance of the wave function in quantum mechanics?
-The wave function in quantum mechanics is a mathematical description of the quantum state of a system. It provides the probabilities of finding a particle in a particular state or location. The wave function is crucial for calculating physical properties and predicting the outcomes of quantum mechanical processes.
Outlines
🎓 Introduction to Harmonic Oscillators
The video begins with an introduction to harmonic oscillators, emphasizing their prevalence in physics. It discusses how systems with an equilibrium state tend to oscillate when displaced, with examples ranging from a violin string to electromagnetic fields. The equilibrium configuration of the radiation field is explained, highlighting the concept of photons as oscillations described by these fields. Creation and annihilation operators are introduced, and their role in quantum mechanics is briefly touched upon.
📐 Hamiltonian Construction and Quantum Corrections
The paragraph delves into the construction of the Hamiltonian for the harmonic oscillator using creation and annihilation operators. It also discusses the quantum mechanical correction to the energy levels, known as the ground state energy or vacuum energy, which is a consequence of the uncertainty principle. The commutation relations of the operators are explored, showing how they lead to the quantization of energy levels in integers.
🤔 Existence and Properties of the Ground State
The speaker argues for the existence of a ground state in the harmonic oscillator system, which is annihilated by the lowering operator. This state is characterized by having zero energy, as it cannot transition to a lower state. The concept of the wave function and its relation to state vectors and operators is introduced, setting the stage for solving the Schrödinger equation for the ground state.
🧮 Solving the Schrödinger Equation for Wave Functions
The focus shifts to solving the Schrödinger equation to find the wave functions that correspond to the energy levels of the harmonic oscillator. The importance of square-integrable wave functions for normalizability and the physical interpretation of the quantum states is emphasized. The process of solving the time-independent Schrödinger equation is outlined, with attention given to the conditions that lead to acceptable wave functions.
🚀 Simplifying the Schrödinger Equation with Annihilation Operator
The paragraph demonstrates a more efficient approach to finding the ground state wave function by using the annihilation operator. It simplifies the Schrödinger equation to a first-order differential equation and employs a trial solution involving an exponential function. The solution is shown to be a Gaussian function, which is square integrable and thus physically acceptable.
🌐 Excited States and Wave Function Behavior
The speaker explores the first excited state of the harmonic oscillator by applying the creation operator to the ground state. The resulting wave function is an odd function, indicating a node at the origin where the probability of finding the oscillator is zero. The behavior of higher excited states is discussed, noting that each successive state has an increasing number of nodes and is pushed further out, reflecting a trade-off between potential and kinetic energy.
🔍 Large Quantum Numbers and Correspondence Principle
The paragraph addresses the correspondence principle in the context of the harmonic oscillator, particularly when quantum numbers become large. It explains that classical behavior is recovered through the formation of wave packets that superpose many energy levels. The time-dependent Schrödinger equation is mentioned to describe the oscillation of these wave packets, which increasingly resemble classical oscillators as energy increases.
🧲 Spin and Its Significance in Quantum Mechanics
The discussion moves on to the concept of spin in quantum mechanics, highlighting its importance in understanding the periodic table and spectroscopy. Spin is introduced as an intrinsic form of angular momentum associated with particles like electrons, protons, and neutrons. The speaker touches upon the historical motivation for introducing spin, which was to explain the structure of the periodic table and the behavior of electrons in atoms.
🎭 Total Angular Momentum and Its Components
The paragraph introduces the total angular momentum, denoted as J, which is the vector sum of orbital angular momentum (L) and spin (S). The concept is illustrated with the Hamiltonian for a system and the commutation relations for angular momentum components. The importance of understanding the addition of angular momentum in quantum mechanics is emphasized, particularly in atomic physics.
🤝 Identical Particles and the Swap Operation
The final paragraph explores the quantum mechanical treatment of identical particles, such as electrons or photons. It defines a swap operation (S) that interchanges the positions of two identical particles and notes that S squared must be equal to one, leading to eigenvalues of either plus one or minus one. This distinction categorizes particles into two types: bosons (integer spin) and fermions (half-integer spin), which have different statistical behaviors when their positions are swapped.
Mindmap
Keywords
💡Harmonic Oscillator
💡Equilibrium State
💡Quantum Mechanics
💡Zero-Point Energy
💡Uncertainty Principle
💡Wave Function
💡Schrodinger Equation
💡Angular Momentum
💡Spin
💡Pauli Exclusion Principle
💡Bosons and Fermions
Highlights
Harmonic oscillators are fundamental in physics, appearing in classical and quantum mechanical systems.
Displacement from equilibrium in a system generally leads to oscillatory behavior, such as in a violin string.
The electromagnetic field's equilibrium configuration is the vacuum, with no oscillations present.
Oscillations of the electromagnetic field are described by photons, which are related to the field's frequencies.
Quantum mechanically, the Hamiltonian for a simple harmonic oscillator can be constructed using creation and annihilation operators.
The ground state energy of a harmonic oscillator, also known as the zero-point energy, arises from the uncertainty principle.
The wave function for the ground state of a harmonic oscillator is a Gaussian function, indicating a high probability near the origin.
Excited states of the harmonic oscillator are characterized by an increasing number of nodes in their wave functions.
The correspondence principle in quantum mechanics states that at high energies, quantum systems resemble classical systems.
Wave packets can be used to demonstrate the classical-like behavior of quantum systems at high energies.
Spin is an intrinsic form of angular momentum associated with particles, such as electrons and protons.
The concept of spin was introduced to explain the structure of the periodic table and certain spectroscopic phenomena.
The Pauli Exclusion Principle states that no two electrons can occupy the same quantum state simultaneously.
Particles can be classified as bosons or fermions, with bosons allowing multiple particles in the same state and fermions following the Pauli Exclusion Principle.
The spin of particles is tested experimentally by observing their behavior in a magnetic field, which can reveal their magnetic moment.
The structure of atoms, as described by quantum mechanics, shows that electrons fill available energy levels starting from the lowest.
The size of atoms does not increase significantly with added electrons due to the balancing effect of increased nuclear charge.
The concept of identical particles in quantum mechanics is fundamental and leads to the classification of particles as either bosons or fermions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: