Calculus Chapter 5 Lecture 50 Infinite Series
TLDRIn this calculus lecture, Professor Greist delves into the intricacies of infinite series, a central topic in the chapter. He introduces the concept by drawing parallels with improper integrals, defining series through the limit of partial sums. The lecture emphasizes the importance of determining convergence or divergence, using examples like geometric and harmonic series to illustrate the subtleties involved. Professor Greist also highlights the limitations of intuition and calculators, advocating for logical and deductive reasoning with specific tests for series analysis, setting the stage for further exploration of convergence tests in upcoming lessons.
Takeaways
- 📚 The lecture introduces the concept of infinite series, a central topic in calculus, which parallels the study of improper integrals.
- 🌟 Infinite series are defined as the limit of the sum of terms as n approaches infinity, similar to the definition of improper integrals.
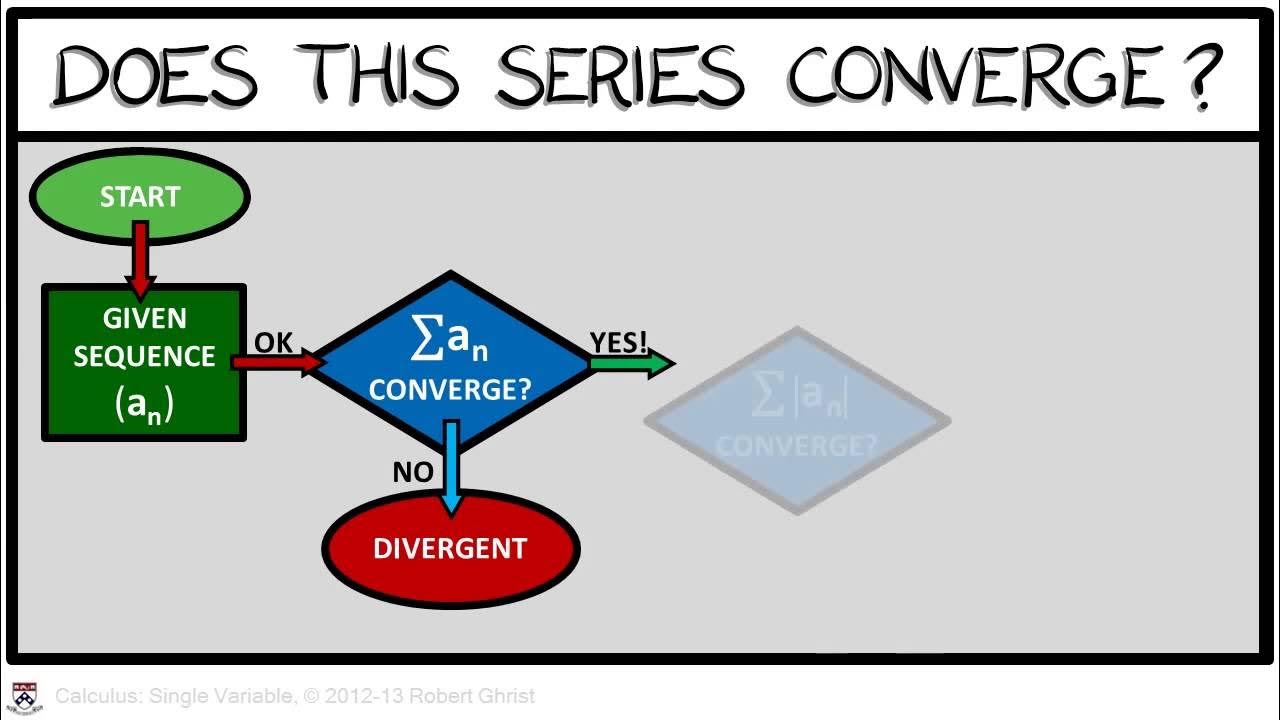
- 🔍 The focus of the lecture is on the convergence or divergence of series, a critical aspect that has been postponed until now.
- 🔢 Examples of series, such as geometric series, are given to illustrate the concepts of convergence and divergence.
- 🔄 The geometric series is shown to converge under certain conditions, but diverge when evaluated at negative values.
- 🧩 The sum of 1 over N squared from 1 to infinity is highlighted as an example of a series that converges but to a value that is not easily determined.
- 📈 The harmonic series is discussed, with calculations showing that it appears to converge but requires more than a calculator to determine its behavior.
- ⚠️ The lecture warns against relying solely on intuition or calculators to determine the convergence or divergence of series, emphasizing the importance of logical reasoning.
- 📉 The harmonic series is compared to the improper integral from 1 to infinity of 1 over X, which is known to diverge, leading to the conclusion that the harmonic series also diverges.
- 🔄 The alternating harmonic series is shown to converge to the logarithm of 2, demonstrating that rearranging terms in a series can affect its convergence.
- 📝 The nth term test is introduced as a logical method for determining divergence if the limit of the nth term as n approaches infinity is non-zero.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is infinite series, which is a central concept in calculus, dealing with the convergence and divergence of series.
How is an infinite series defined in terms of improper integrals?
-An infinite series is defined similarly to an improper integral by considering it as a limit of the sum of terms as n goes to infinity, analogous to the limit of a definite integral as the upper bound goes to infinity.
What is the significance of the convergence or divergence of an infinite series?
-The convergence or divergence of an infinite series is significant as it determines whether the series has a finite sum or if it grows without bound, which is a fundamental concept in calculus.
Can you provide an example of a geometric series and its convergence?
-An example of a geometric series is 1 + 1/e + 1/e^2 + 1/e^3 + ..., which converges to a specific value because it follows the pattern of a geometric progression with a common ratio less than 1.
What is the harmonic series and why is it divergent?
-The harmonic series is the sum of the reciprocals of the natural numbers, 1 + 1/2 + 1/3 + 1/4 + ..., and it is divergent because the terms do not approach zero quickly enough to allow the series to converge to a finite sum.
How does the nth term test for convergence or divergence work?
-The nth term test states that if the limit of the nth term as n approaches infinity is not equal to zero, then the series diverges. However, if the limit is zero, it does not guarantee convergence.
What is the contrapositive of the nth term test and why is it important?
-The contrapositive of the nth term test is that if a series converges, then the limit of the nth term as n approaches infinity is zero. It is important because it is always true and helps in logical reasoning about the convergence of a series.
Why is a calculator not a reliable tool for determining convergence or divergence?
-A calculator is not reliable for determining convergence or divergence because it can only provide the sum of the first few terms of a series, which may not be indicative of the series' behavior as more terms are added.
What is the relationship between the harmonic series and the improper integral from 1 to infinity of 1/x dx?
-The harmonic series can be seen as a discretization of the improper integral from 1 to infinity of 1/x dx, which is known to diverge. This relationship helps in understanding why the harmonic series also diverges.
Why is it important to use logic and deductive reasoning in determining the convergence or divergence of a series?
-Logic and deductive reasoning are important because they provide a consistent and reliable method to determine the convergence or divergence of a series, unlike intuition or calculator-based approximations, which can be misleading.
What is the alternating harmonic series and to what value does it converge?
-The alternating harmonic series is the series 1 - 1/2 + 1/3 - 1/4 + 1/5 - ..., and it converges to the value of the natural logarithm of 2, demonstrating the subtlety of convergence in series.
Outlines
📚 Introduction to Infinite Series in Calculus
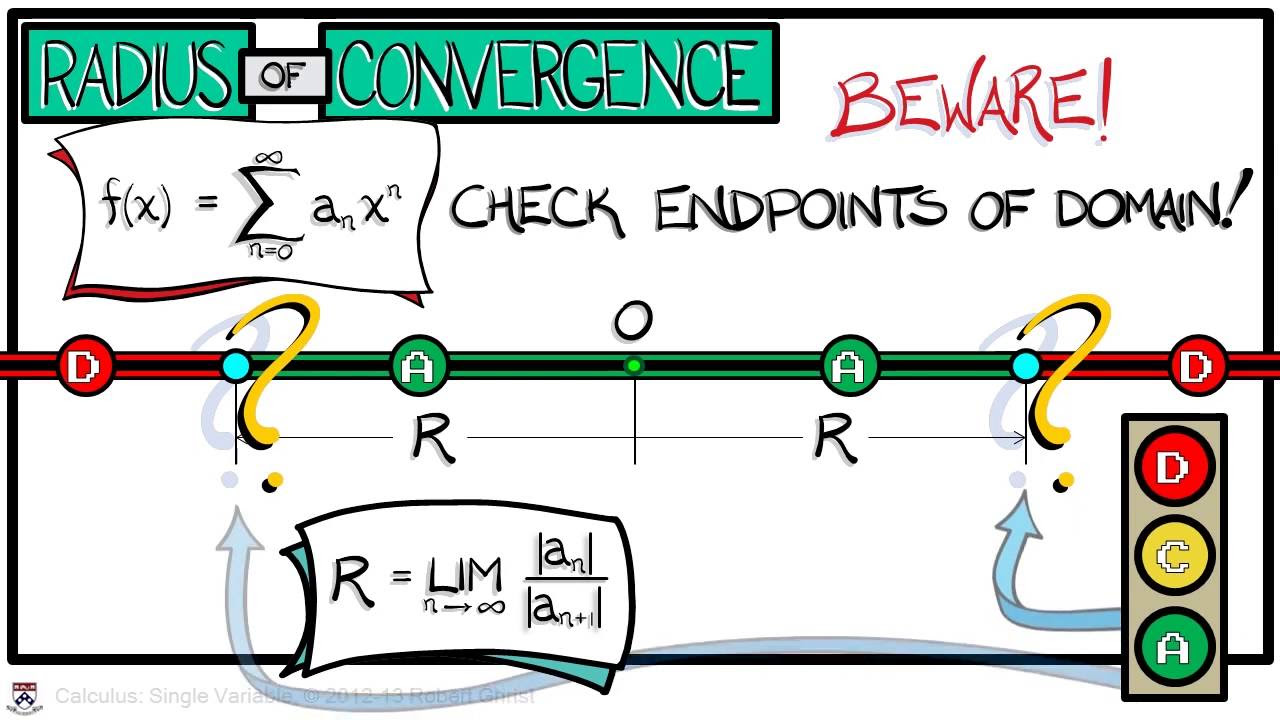
Professor Greist begins lecture 50 by introducing the concept of infinite series, which are central to the current chapter on calculus. He compares these series to improper integrals, explaining that they are defined through limits, similar to how the integral from 1 to infinity of f(x) dx is defined. The lecture aims to explore the convergence and divergence of series, building upon the understanding of sequences and their analogs to improper integrals. The professor emphasizes the importance of understanding these concepts, which have been a recurring theme throughout the course, and promises to address them in detail, providing ample practice for students to master the topic.
🔍 Analyzing Convergence and Divergence of Series
In this segment, the professor delves into the nuances of series convergence and divergence, using the geometric series as an example to illustrate convergence and the series at negative one to demonstrate divergence due to oscillation. He then discusses the subtle convergence of the series summing 1/n^2 to π^2/6, highlighting the difficulty in determining exact sums. The harmonic series, 1 + 1/2 + 1/3 + ..., is examined with the aid of a computer to show that despite adding a large number of terms, convergence is not evident. The professor uses this to transition into a discussion about the limitations of calculators and intuition in determining convergence, advocating for the use of calculus intuition instead.
📉 The Harmonic Series and Calculus Intuition
The professor continues by focusing on the harmonic series, comparing it to the improper integral from 1 to infinity of 1/x dx, which is known to diverge. Using a left Riemann sum analogy, he concludes that the harmonic series must also diverge. This example serves to demonstrate how continuous calculus understanding can be applied to discrete calculus problems. The discussion then shifts to the reliability of tools and intuition in determining convergence or divergence, with the professor emphasizing that while intuition can be flawed, logical and deductive reasoning based on calculus tests is the most trustworthy approach.
📝 Trusting Logic and Deductive Reasoning in Series Analysis
The final paragraph introduces the concept of logical and deductive reasoning in the analysis of series. The professor presents the nth term test as a method for determining divergence, explaining its application and limitations. He uses examples to illustrate how the test can be applied and cautions against relying on the converse of the test, which does not always hold true. The professor concludes by emphasizing the importance of following logical rules to avoid errors in the analysis of series convergence and divergence, and hints at the introduction of more specific tests in upcoming lessons.
Mindmap
Keywords
💡Infinite Series
💡Convergence
💡Divergence
💡Geometric Series
💡Harmonic Series
💡Improper Integral
💡Partial Sums
💡nth Term Test
💡Alternating Harmonic Series
💡Logarithm
💡Riemann Sum
Highlights
Introduction to Lecture 50 on infinite series, emphasizing their importance in calculus.
Comparison of infinite series to improper integrals, using limits to define series convergence.
Explanation of the concept of convergence and divergence in the context of infinite series.
Illustration of geometric series convergence and its sum calculation.
Demonstration of a divergent geometric series with a negative ratio.
Introduction of the series 1/n^2 and its convergence to a specific value, π^2/6.
Discussion on the difficulty of determining the convergence of the harmonic series.
Use of a computer simulation to investigate the behavior of the harmonic series.
Comparison of the harmonic series to the improper integral of 1/x from 1 to infinity.
Misleading nature of calculators and intuition in determining series convergence or divergence.
Introduction of the alternating harmonic series and its convergence to log(2).
The importance of logical deductive reasoning over intuition in mathematical analysis.
Description of the nth term test for series convergence or divergence.
Limitations of the nth term test and the importance of logical application.
The contrapositive logic in understanding the nth term test's implications.
Announcement of upcoming lessons on specific tests for measuring convergence and divergence of infinite series.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: