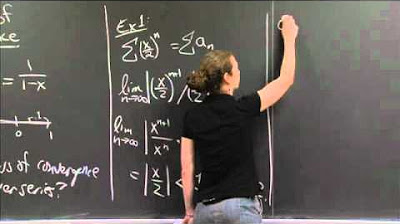Calculus Chapter 5 Lecture 54 Power Series
TLDRIn this calculus lecture, Professor Greist delves into the concept of power series, explaining how they convert sequences into functions. He illustrates this with examples, including geometric and Fibonacci series, and discusses the importance of the radius of convergence for determining the series' behavior. The lecture also covers the ratio test for convergence and provides insights into the convergence properties of various series, setting the stage for further exploration of Taylor series in upcoming lessons.
Takeaways
- 📚 The lecture introduces the concept of power series and how they can be used to convert sequences into functions.
- 🔍 Power series are defined as a series with the variable X inside as a monomial term, such as \( \sum_{n=0}^{\infty} a_n X^n \).
- 🌟 Examples of power series include monomials, polynomials, and the geometric series, which converges to \( \frac{1}{1-X} \) for \( |X| < 1 \).
- 🔑 The power series can represent various functions, such as logarithmic and exponential functions, through specific sequences.
- 🔄 The Fibonacci sequence, when used as coefficients in a power series, can be manipulated to align with its recursive relation and converge to a specific function.
- 🔢 The convergence of a power series is determined by the radius of convergence, a special number that indicates the range of X values for which the series converges.
- 📉 The ratio test is used to determine the convergence of a power series by examining the limit of the ratio of consecutive terms.
- 📌 The endpoints of the convergence domain require special attention as the ratio test does not provide information about them.
- 📐 Shifted power series are a form of power series centered at a point other than zero, and they converge within a certain distance from the center.
- 📈 The radius of convergence is calculated using the limit of the ratio of the absolute values of consecutive coefficients, indicating the series' divergence outside this radius.
- 🔮 Upcoming lectures will focus on Taylor series, a specific type of power series derived from smooth functions.
Q & A
What is a power series?
-A power series in X is a series that has the variable X inside of it as a monomial term, typically expressed as the sum from n=0 to infinity of a_n * X^n, where a_n are coefficients.
How can a power series be viewed in terms of functions and sequences?
-A power series can be viewed as an operator that converts a sequence of coefficients, a_n, into a function f(x).
What is the geometric series and its corresponding function in terms of power series?
-The geometric series corresponds to the sequence of all ones and gives the function 1/(1-x) for |x| < 1.
How do you determine the convergence behavior of a power series?
-The convergence behavior of a power series can be determined by the radius of convergence, R. The series converges absolutely if |x| < R and diverges if |x| > R.
What is the ratio test and how is it used in the context of power series?
-The ratio test is used to determine the convergence of a power series. It involves computing the limit as n approaches infinity of the absolute value of the ratio of the n+1 term to the nth term. If this limit is less than 1, the series converges absolutely; if greater than 1, it diverges.
What does the radius of convergence represent?
-The radius of convergence represents the distance from zero within which the power series converges absolutely. Outside this radius, the series diverges.
What is the radius of convergence for the power series with coefficients 1/n?
-The radius of convergence for the power series with coefficients 1/n is 1. At the right endpoint (x=1), the harmonic series diverges, while at the left endpoint (x=-1), the alternating harmonic series converges conditionally.
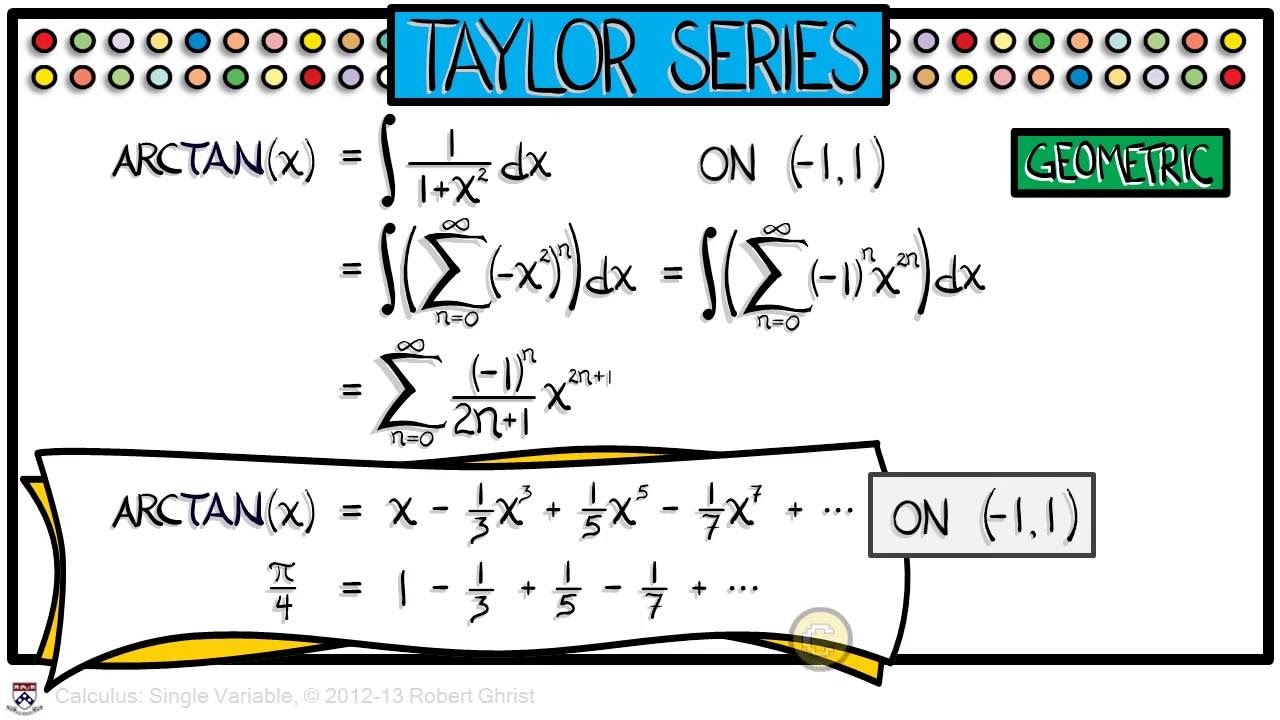
How can the Fibonacci sequence be represented as a power series?
-The Fibonacci sequence can be represented as a power series by denoting the series as script F. By manipulating the series using shifts and the recursion relation, it is found that script F = x / (1 - x - x^2).
What happens at the endpoints of the radius of convergence?
-The ratio test does not provide information about the endpoints of the radius of convergence. Each endpoint must be checked explicitly for convergence or divergence.
What is a shifted power series and how is its radius of convergence determined?
-A shifted power series is of the form sum over n of a_n * (x-c)^n, where c is a shift from zero. The radius of convergence is determined in the same way as for a regular power series, and it converges for |x-c| < R.
Outlines
📚 Introduction to Power Series
Professor Greist kicks off the lecture by introducing the concept of power series as a tool to convert sequences into functions. He explains that a power series is a series with a variable inside it as a monomial term and uses simple examples to illustrate the concept. The professor also introduces the idea of a power series as an operator that transforms sequences into functions. He discusses the power series for sequences like all zeros except one, finite sequences, and the sequence of all ones, which corresponds to the geometric series. The lecture touches on how sequences like the Fibonacci sequence can be represented by power series and how these series can be manipulated to align with recursive relations.
🔍 Exploring Convergence and the Radius of Convergence
This section delves into the convergence behavior of power series. The professor discusses the importance of the radius of convergence, denoted by R, and explains how it dictates the region where a power series converges absolutely. The ratio test is introduced as a method to determine the convergence of a series, with the limit of the ratio of successive terms indicating the behavior of the series. The professor also emphasizes the need to check the endpoints of the convergence domain, as the ratio test does not provide information about them. Examples are given to illustrate the computation of the radius of convergence and the behavior of series at the endpoints.
📉 Examples of Power Series and Their Convergence
The third paragraph provides examples of different power series and their convergence properties. The professor discusses the power series with coefficients that grow, such as the series with coefficients 1/N^2, and how they converge at both endpoints. He also introduces the concept of a shifted power series and explains how to determine its radius of convergence. A specific example is given, involving a series that is manipulated algebraically to fit the form of a shifted power series, and the process of determining its radius of convergence is outlined.
🌟 Shifted Power Series and Upcoming Topics
In the final paragraph, the professor wraps up the discussion on shifted power series by providing an example and explaining how to determine its domain of convergence. He also previews the next topic, which will be Taylor series, a special type of power series derived from smooth functions. The professor hints at the importance of Taylor series in understanding the behavior of functions and their applications in mathematics.
Mindmap
Keywords
💡Power Series
💡Convergence
💡Radius of Convergence
💡Ratio Test
💡Geometric Series
💡Fibonacci Sequence
💡Absolute Convergence
💡Polynomial
💡Shifted Power Series
💡Taylor Series
Highlights
Introduction to the concept of power series and its role in converting sequences into functions.
Explanation of power series as a series with the variable X inside as a monomial term.
The idea of power series as an operator that transforms the sequence a_n into a function f(X).
Examples of power series for simple sequences, including a monomial for a sequence with a single non-zero term.
Description of polynomials as finite power series with coefficients in front of monomials that terminate.
The geometric series as an example of a power series for the sequence of all ones.
Correspondence of certain sequences to well-known functions like logarithms and exponentials.
Analysis of a sequence that does not go to zero and its relation to the function 1/(1+x^2).
The mystery of convergence for arbitrary sequences of coefficients and the example of the Fibonacci sequence.
The process of aligning coefficients to match the recursion relation of the Fibonacci sequence in power series.
Derivation of the power series formula for the Fibonacci sequence as x/(1 - x - x^2).
Discussion on the practical applications and theoretical implications of power series functions.
The theorem on the convergence behavior of power series for a given radius R.
Use of the ratio test to determine the convergence of power series and the significance of the radius of convergence.
Explanation of the radius of convergence as a measure of the distance from zero beyond which the series diverges.
Procedure to check convergence at the endpoints of the domain, as the ratio test is inconclusive there.
Examples of different power series and their behavior at the endpoints, including divergence and conditional convergence.
Introduction to shifted power series and their convergence criteria relative to a center point C.
An example of determining the radius of convergence for a shifted power series involving algebraic manipulation.
Upcoming focus on Taylor series, a specific type of power series derived from smooth functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: