Calculus Chapter 4 Lecture 40 Centroids & Centers
TLDRIn this calculus lecture, Professor Greist delves into the concept of centroids and centers of mass, illustrating how to compute average positions within a region using calculus. The lecture introduces formulas for calculating the centroid coordinates (X bar and Y bar) through double integrals and demonstrates their application with examples, such as a quarter disk and a right triangle. The importance of respecting domain symmetries in centroid calculations is highlighted, and the lecture concludes with an exploration of center of mass, showing its relevance in physics and chemistry.
Takeaways
- 📍 Averages appear in many forms and sizes; in this lesson, we're computing average positions, leading to centroids and centers of mass.
- 📐 The centroid is the average location in a domain, defined by the coordinates X bar and Y bar, representing the average x and y coordinates.
- 🧮 To find the centroid, we use double integrals over the domain, dividing it into infinitesimal rectangles of dimensions dx and dy.
- 🔍 For regions between two curves, the formula for X bar involves integrating x times the area element over the region.
- ⚖️ The formula for Y bar is slightly different, involving the integral of y dy, leading to y squared over 2 in the numerator.
- 🔄 Symmetry in a domain can simplify centroid calculations, as centroids lie along axes of symmetry or at their intersections.
- 📏 For specific shapes like triangles or quarter disks, centroids have predictable locations based on symmetry and area.
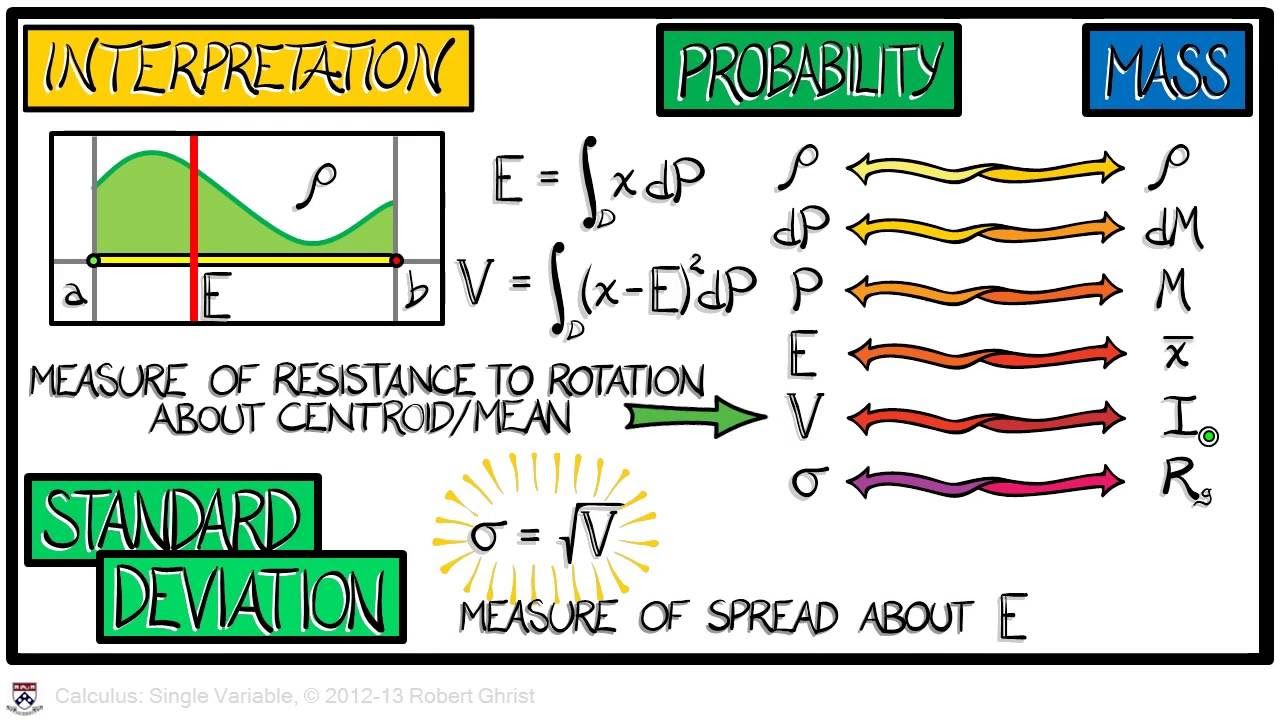
- 📊 Centroids and centers of mass are closely related; the center of mass involves weighting the average location by the mass element.
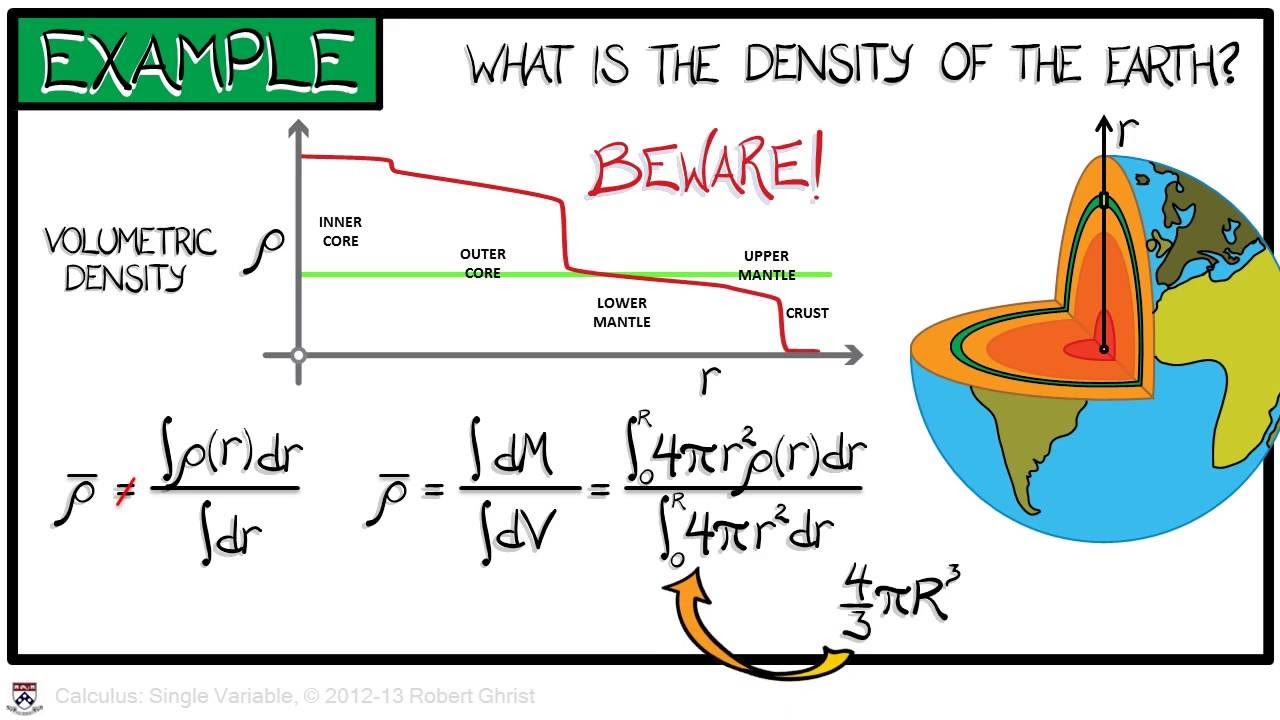
- 📈 A simple example with a varying density shows how to compute the center of mass, which differs from the centroid due to the mass distribution.
- 🔧 Using centroids can simplify computations for volumes, forces, and other physical properties, especially when combined with moments of inertia.
Q & A
What is the main topic of this calculus lecture?
-The main topic of this calculus lecture is centroids and centers of mass, focusing on how to compute average positions in various domains using calculus.
How is the average location of two points determined?
-The average location of two points is determined by drawing the line segment between them and picking the point in the middle.
What is the formula for X-bar in terms of a domain D?
-X-bar is the average x-coordinate over the domain D, calculated as the integral of x over D divided by the integral of one over D.
What is the significance of the double integral in determining the centroid?
-The double integral is used to break the region into infinitesimal elements and compute the average position by integrating over these elements with respect to the area element.
How is the area element represented in the context of a region between two curves?
-The area element in the context of a region between two curves is represented as an infinitesimal rectangle of dimensions dx and dy.
What is the formula for Y-bar in terms of a domain D?
-Y-bar is the average y-coordinate over the domain D, calculated as half the integral of y squared over D divided by the integral of one over D.
How does the centroid computation differ for a quarter disk of radius R?
-For a quarter disk of radius R, the centroid computation involves integrating x and y with respect to the area element, taking into account the specific geometry of the quarter disk.
What principle do centroids respect in terms of symmetry?
-Centroids respect the symmetries implicit in a domain; if there is an axis of symmetry, the centroid lies along it, and if there are two axes of symmetry, the centroid lies at their intersection.
How is the centroid of a right triangle with height H and length L determined?
-The centroid of a right triangle is located one-third of the way in from each of the three sides, which can be determined by integrating the appropriate expressions for X-bar and Y-bar.
What is the concept of center of mass and how is it related to centroids?
-The center of mass is the average location of mass elements in a body, and it is related to centroids in that both concepts involve averaging positions, but the center of mass takes into account the mass distribution.
How can thinking in terms of centers of mass simplify centroid computations?
-Thinking in terms of centers of mass can simplify centroid computations by allowing one to break a region into pieces, focus the areas at their centroids, and compute the weighted center of mass, which can make the problem easier.
Outlines
📚 Introduction to Calculus of Centroids
Professor Greist begins lecture 40 by introducing the concept of centroids and centers of mass, explaining how to compute average positions in various shapes and sizes. He simplifies the process by starting with the average of two points and then extends it to entire regions using calculus, breaking down regions into infinitesimal elements. The centroid is defined as the average location within a domain, characterized by coordinates X bar and Y bar, which are derived from integrals over the domain. The lecture also touches on higher-dimensional settings and the use of double integrals to find centroids, with the denominator representing the area element, leading to a formula for the centroid based on the integral of x or y over the domain divided by the integral of one over the domain.
🔍 Detailed Calculation of Centroids
The script continues with a detailed explanation of how to calculate the centroid of a region bounded by two curves, g and f, as x varies from A to B. The area element is considered as an infinitesimal rectangle, and the formula for X bar is derived through double integrals, with the limits of integration determined based on the curves' boundaries. The process involves integrating with respect to y first, using the curves as limits, and then integrating with respect to x from A to B. The formula for X bar is simplified to an integral involving the area between the curves, which is a key formula to remember. A similar but distinct process is used to calculate Y bar, with the main difference being the integration of Y dy instead of X dy, leading to a different final formula. The lecture provides a specific example of a quarter disk to illustrate the calculation process.
📐 Centroid Calculation in Symmetric Shapes
The script discusses the computation of centroids in symmetric shapes, such as a quarter circle, and how symmetry can simplify the process. It demonstrates that the centroid of a quarter circle lies on the line y equals x by calculating X bar and Y bar using the area under the curve and the integral formulas. The example of a right triangle is also explored, showing that the centroid is located one-third of the way in from each side, a result that can be derived from considering the mass at the vertices and averaging their coordinates. The concept of focusing mass is introduced as a common approach in physics and chemistry for representing locations of objects, leading to the notion of a center of mass, which is calculated by integrating with respect to mass rather than area.
🔄 Application of Centroids and Centers of Mass
The final paragraph highlights the practical applications of centroids and centers of mass, mentioning their utility in computing volumes and forces, and their role in moments of inertia. The script suggests that thinking in terms of centers of mass can simplify centroid computations by breaking a region into pieces and focusing the areas at their centroids, weighted by the area of each piece. It also touches on the concept of negative areas and mass, which can further simplify computations. The lecture concludes by encouraging students to explore the bonus material for more applications of centroids in solid bodies and moments of inertia.
Mindmap
Keywords
💡Centroid
💡Center of Mass
💡Integral
💡Average
💡Symmetry
💡Infinitesimal Elements
💡Double Integral
💡Iterated Integral
💡Area Element
💡Right Triangle
💡Moments of Inertia
Highlights
Introduction to the concept of centroids and centers of mass in calculus.
Explaining the computation of average positions leading to the notion of centroids.
The definition of a centroid as the average location in a domain D.
Formula for calculating the centroid's coordinates X bar and Y bar using integrals.
Application of calculus to break a region into infinitesimal elements for average computation.
Use of double integrals and iterated integrals in calculating centroids.
Explanation of the integral of 1 over the domain as the integral with respect to the area element.
Demonstration of calculating the centroid of a region between two curves.
Integration technique using limits of integration to find X bar and Y bar.
The formula for X bar in terms of the area between two curves.
Difference in the formula for Y bar involving the integral of Y squared.
Example of calculating the centroid of a quarter disk using the derived formulas.
The principle that centroids respect the symmetries of a domain.
Calculation of the centroid for a right triangle using integral formulas.
General principle that the centroid of any triangle is one-third of the way in from each side.
Introduction to the concept of center of mass and its relation to centroids.
Method of calculating the center of mass using the mass element and its integral.
Example of finding the center of mass for a one-dimensional object with varying density.
Discussion on the practical applications of centroids and centers of mass in physics and chemistry.
Technique of using centroids and areas to simplify complex centroid computations.
Continuation of the exploration of solid bodies in the next lesson with moments of inertia.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: