Calculus Chapter 3 Lecture 26 The FTIC
TLDRIn this calculus lecture, Professor Greist delves into the Fundamental Theorem of Integral Calculus, illustrating its significance in bridging definite and indefinite integrals. He demonstrates how this theorem simplifies the computation of integrals through examples, such as calculating the area under a curve and the change in profit for a publisher. The lecture also covers the interpretation of the theorem in various contexts, including economics, and highlights the importance of careful limit handling during integration. The professor emphasizes the theorem's utility in simplifying complex computations and foreshadows potential issues when the theorem is pushed to its limits.
Takeaways
- 📚 The Fundamental Theorem of Integral Calculus establishes an equivalence between definite and indefinite integrals, showing they are two aspects of the same concept.
- 🔍 For a continuous function on an interval, the definite integral from A to B is equal to the evaluation of the indefinite integral (antiderivative) of the function at B minus its evaluation at A.
- 📉 The definite integral can be thought of as the area under the curve, while the indefinite integral represents the family of antiderivatives.
- 📝 The theorem simplifies the computation of definite integrals by using antiderivatives, as demonstrated with the example of integrating x with respect to x from A to B.
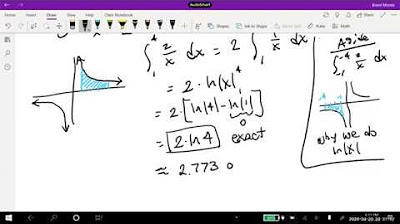
- 🌐 The fundamental theorem provides a new interpretation of natural logarithms, showing that ln(T) can be seen as the area under the curve 1/x from 1 to T.
- 📈 The theorem has broad applications, including economics, where it can be used to understand the relationship between marginal quantities and net changes, such as in supply and demand.
- 📊 The script uses an example of a publisher's production costs and revenues to illustrate how the fundamental theorem can be applied to calculate changes in profit.
- 🤔 The importance of careful limit labeling is highlighted in the context of integration techniques, especially when using substitution methods.
- 🔢 An example of integrating a function involving x(x - 1)^n demonstrates the process of solving definite integrals using substitution and integration by parts.
- ⚠️ The need for caution is emphasized when applying integration by parts, particularly in correctly evaluating the limits of integration.
- 🚀 The fundamental theorem is a powerful tool for computing definite integrals and will be essential for applications in later chapters of the calculus course.
Q & A
What is the main focus of lecture 26 by Professor Greist?
-The main focus of lecture 26 is the introduction and explanation of the Fundamental Theorem of Integral Calculus, which establishes an equivalence between definite and indefinite integrals.
What is the Fundamental Theorem of Integral Calculus?
-The Fundamental Theorem of Integral Calculus states that for a continuous function on the interval from A to B, the definite integral of f(x) dx from A to B is equal to the indefinite integral of F evaluated from A to B, where F is an antiderivative of f(x).
How does the Fundamental Theorem of Integral Calculus simplify computations?
-The Fundamental Theorem simplifies computations by allowing one to find the definite integral of a function by simply finding an antiderivative of the function and then evaluating it at the limits of integration.
What is the geometric interpretation of the natural logarithm in the context of the definite integral from 1 to t of 1/x dx?
-The geometric interpretation of the natural logarithm in this context is that it represents the area under the curve of 1/x as x goes from 1 to t.
How does the Fundamental Theorem of Integral Calculus relate to the concept of marginal quantities in economics?
-The Fundamental Theorem of Integral Calculus relates to marginal quantities in economics by showing that the net change in a quantity, such as supply, is equal to the integral of its rate of change, or the marginal quantity.
What is the example given in the script to illustrate the use of the Fundamental Theorem in economics?
-The example given is about a publisher who prints books with a marginal cost function and a fixed revenue per book. The script explains how to calculate the change in profit resulting from a 25% increase in production by integrating the profit element.
What is the importance of being careful with limits when applying integration techniques?
-Being careful with limits is crucial to ensure that the correct variable and its corresponding limits are used during the integration process, which directly affects the accuracy of the result.
How does the script illustrate the potential confusion with limits when using substitution in integration?
-The script uses the example of integrating x(x - 1)^n dx and explains how one might mistakenly use x = 0 to 1 as the limits instead of correctly changing them to u = -1 to 0 when substituting u = x - 1.
What is the alternative method to substitution mentioned in the script for solving the integral of x(x - 1)^n dx?
-The alternative method mentioned is integration by parts, where one would let u be x and dv be (x - 1)^n dx, and then apply the integration by parts formula to find the integral.
How does the script emphasize the importance of understanding the meaning behind the Fundamental Theorem of Integral Calculus?
-The script emphasizes the importance by discussing several interpretations of the theorem, such as the net change in a quantity being equal to the integral of its rate of change, and by providing examples from various contexts, including physics and economics.
What is the potential issue with the Fundamental Theorem of Integral Calculus when it is pushed to the limit, as hinted at the end of the script?
-The script suggests that while the Fundamental Theorem is extremely useful, there may be situations or limits where it can run into problems, indicating that there are potential exceptions or complexities not covered in the lecture.
Outlines
📚 Introduction to the Fundamental Theorem of Integral Calculus
Professor Greist introduces Lecture 26, focusing on the Fundamental Theorem of Integral Calculus. He clarifies that although definite and indefinite integrals may seem distinct, they are closely related and represent two facets of the same concept. The lecture aims to explore this relationship, demonstrating that the definite integral of a continuous function from A to B is equivalent to the indefinite integral evaluated at those points. The professor uses the example of the integral of X with respect to X from A to B to illustrate the theorem's simplicity and utility, and how it can be applied to compute areas under curves and other integrals.
📈 Multiple Interpretations and Applications of the Fundamental Theorem
The second paragraph delves into various interpretations of the fundamental theorem, emphasizing its broad applicability across different contexts. It highlights the theorem's expression as the net change in a quantity F being equal to the integral of its rate of change. Examples include the relationship between position and velocity, as well as economic scenarios involving marginal costs and revenues. A detailed example of a publisher's profit calculation with variable production levels is provided, showcasing how the theorem can be applied to calculate changes in profit by integrating the profit element over a range of production quantities.
🔍 Caution with Limits in Integration Techniques
In the third paragraph, the professor warns about the importance of carefully handling limits when applying integration techniques. An example is given involving the integral of x times (x - 1) to the power of n, where n is a positive integer. The professor demonstrates two methods of solving this integral: substitution and integration by parts. He emphasizes the need to correctly label and transform limits when changing variables to avoid confusion and ensure accurate results.
🚀 The Power and Limitations of the Fundamental Theorem
The final paragraph of the script acknowledges the power of the Fundamental Theorem of Integral Calculus in simplifying the computation of definite integrals and its role in various applications. However, it also foreshadows potential issues that may arise when the theorem is pushed to its limits, hinting at the complexities that will be explored in the next lecture. The professor encourages students to appreciate the theorem's utility while also being aware of its boundaries.
Mindmap
Keywords
💡Fundamental Theorem of Integral Calculus
💡Definite Integral
💡Indefinite Integral
💡Antiderivatives
💡Riemann Sum
💡Marginal Cost
💡Marginal Revenue
💡Integration by Parts
💡Net Change
💡Limit of Integration
💡Natural Logarithm
Highlights
Introduction to Lecture 26 on the Fundamental Theorem of Integral Calculus.
Definite and indefinite integrals, though seemingly different, are closely related aspects of the same concept.
The fundamental theorem links definite integrals to the evaluation of indefinite integrals from A to B.
The definite integral is a number, while the indefinite integral is a class of antiderivatives.
The equivalence between integrals is demonstrated through the evaluation of antiderivatives at points A and B.
The fundamental theorem simplifies computations by allowing the use of antiderivatives to find definite integrals.
Example of using the fundamental theorem to compute the integral of X DX from A to B, resulting in B squared minus A squared.
Geometric interpretation of the natural logarithm as the area under the curve 1/X from 1 to T.
The fundamental theorem's importance in understanding the relationship between a function and its rate of change.
Practical applications of the theorem in various contexts, such as physics and economics.
An example of calculating the change in profit for a publisher with a given marginal cost function.
The process of setting up an integral problem with marginal cost and revenue functions to find profit changes.
The importance of careful labeling when changing limits in integration, demonstrated through an example.
Solving the integral of x times (x - 1) to the power of n using substitution and integration by parts.
The correct application of limits when changing variables in an integral, crucial for obtaining accurate results.
Integration by parts formula for definite integrals and its careful application with respect to limits.
The fundamental theorem's potential limitations when pushed to extreme cases, to be discussed in the next lecture.
Transcripts
Browse More Related Video

Lec 22: Green's theorem | MIT 18.02 Multivariable Calculus, Fall 2007

Calculus 1: Indefinite Integrals and the Net Change Theorem (Section 5.4) | Math with Professor V

Calculus - The Fundamental Theorem, Part 1

Unit II: Lec 9 | MIT Calculus Revisited: Single Variable Calculus

Definite Integrals!
Math 11 - Section 4.3
5.0 / 5 (0 votes)
Thanks for rating: