Calculus Chapter 1 Lecture 3 Taylor Series
TLDRIn this calculus lecture, Professor Gist introduces Taylor series as a powerful tool to express functions as series. Starting with the series representation of e^x, the concept is extended to trigonometric functions like sine and cosine. The Taylor series definition is highlighted, showing how to compute coefficients by evaluating derivatives at zero and dividing by factorials. Examples include deriving series for e^x, sine, and cosine, and applying the method to a simple polynomial. The video also touches on the Bessel function, j0, defined through its Taylor series, illustrating its relevance in real-world phenomena like the shape of a rotating chain. The lecture concludes with the advantages of using Taylor series for function approximation.
Takeaways
- 📚 The lecture introduces the concept of Taylor series as a method to express functions as infinite series, leveraging the understanding of e^x as a series.
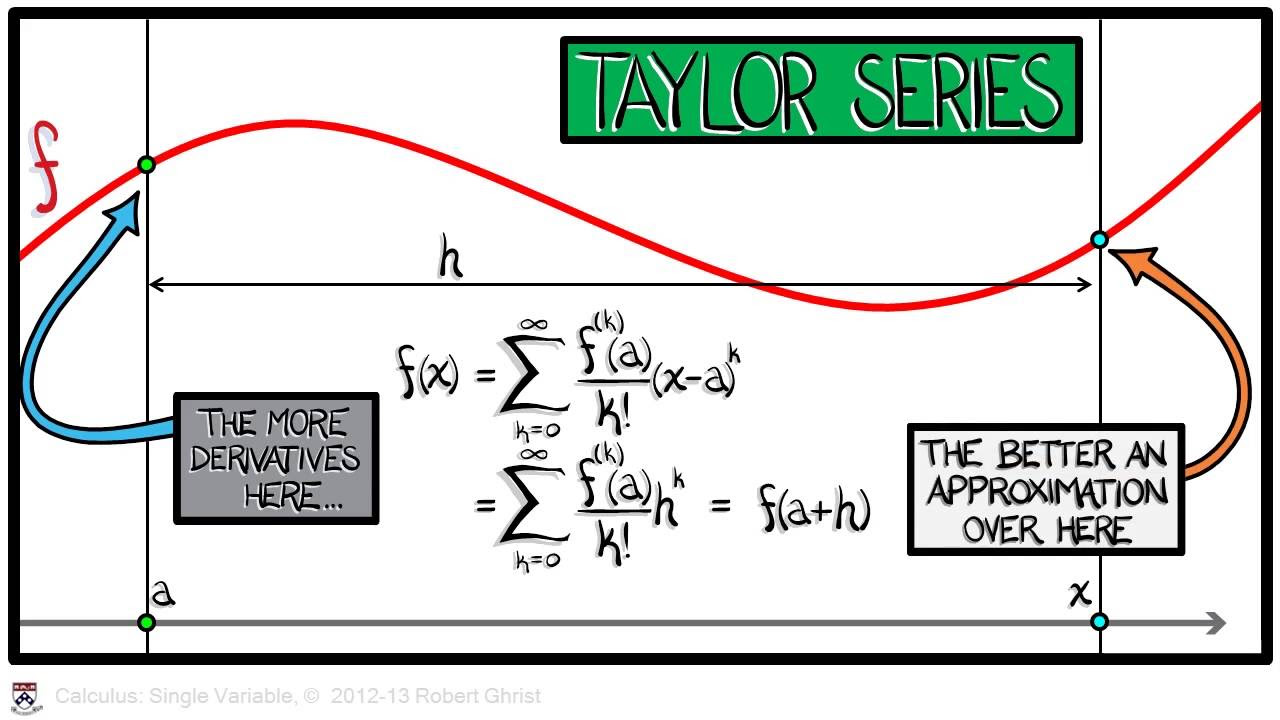
- 🔍 The Taylor series of a function at an input zero is defined as a sum involving the function's derivatives at that point, divided by increasing factorials.
- 📈 The kth coefficient of the Taylor series is calculated as the kth derivative of the function evaluated at the input, divided by k factorial.
- 🌟 The series can be used to approximate functions that are difficult to work with directly, simplifying complex functions into a form that is easier to handle.
- 📝 The script provides an example of applying the Taylor series to e^x, showing how it results in the familiar exponential series.
- 📉 The process is also demonstrated for the sine function, revealing its series expansion with alternating signs and terms that repeat every four powers of x.
- 📐 The cosine function's Taylor series is shown to have only even-powered terms due to the derivatives evaluated at zero.
- 🔢 A polynomial function is used to illustrate that polynomials themselves have their own Taylor series, which is identical to the polynomial when expanded.
- 🎓 The Bessel function j0 is introduced as an example of a function defined by its Taylor series, highlighting its relevance in physical phenomena like vibrating ropes.
- 📊 The Bessel function's series reveals a pattern similar to cosine but with rapidly increasing denominators, suggesting a wave-like graph with decreasing amplitude.
- 🔧 The Taylor series can be used to approximate functions for small values of x, as demonstrated with the Bessel function's application to the displacement of a rotating rope.
Q & A
What is the main topic of Lecture Three in the calculus course taught by Professor Gist?
-The main topic of Lecture Three is Taylor series, focusing on extending the understanding of e^x as a series to other functions using the concept of Taylor series.
What is the significance of the Taylor series in the context of this lecture?
-The Taylor series is significant as it allows for the expression of functions in the form of a series, simplifying complex functions into a more manageable polynomial or series form.
What is the definition of the Taylor series of a function at an input zero?
-The Taylor series of a function at an input zero is a series that starts with the function value at zero and adds terms involving the derivatives of the function at zero, each divided by the factorial of the term's degree.
How are the coefficients of the Taylor series computed?
-The coefficients of the Taylor series are computed by evaluating the kth derivative of the function at the input point (in this case, zero) and dividing by k factorial.
What is the relationship between the derivatives of e^x and the resulting Taylor series for e^x?
-Since the derivative of e^x is always e^x, all derivatives evaluate to one when substituted into the formula for the Taylor series, resulting in the familiar series for e^x.
How does the Taylor series for sine (sin(x)) differ from that of cosine (cos(x))?
-The Taylor series for sine and cosine differ in the signs of their terms. Sine has alternating signs starting with a positive term, while cosine has a series with alternating signs starting with a negative term due to the sequence of derivatives evaluated at zero.
Why is the Taylor series for a polynomial function the same as the polynomial itself?
-The Taylor series for a polynomial function is the same as the polynomial itself because the derivatives of a polynomial at zero yield the coefficients of the polynomial in ascending order of degree, resulting in the original polynomial when written out.
What is the Bessel function, and how is it defined in terms of its Taylor series?
-The Bessel function, specifically j0, is a function that is most easily defined in terms of its Taylor series, which involves a sum of terms with coefficients that have a complex pattern involving factorials and powers of x.
How can the Bessel function be related to everyday occurrences, such as the shape of a chain or rope when rotated?
-The Bessel function is related to the shape of a chain or rope when rotated around a vertical axis, as the displacement from the vertical axis can be described using the Bessel function, showing a pattern similar to a cosine wave with decreasing amplitude.
What insight can be gained from the Taylor series of the Bessel function when considering small values of x?
-When considering small values of x, the Taylor series of the Bessel function simplifies to a linear expression in x, indicating that the slope at the end of a rotating rope is proportional to the square of the angular frequency, showing a quadratic relationship.
What is the next step in the course after understanding the definition and advantages of Taylor series?
-The next step in the course is to consider how to effectively compute Taylor series, which will be the focus of the next lecture.
Outlines
📚 Introduction to Taylor Series
Professor Gist introduces the concept of Taylor series in calculus, using the understanding of e^x as a series to extend this idea to other functions. The lecture begins with the assumption that any 'reasonable' function can be expressed as a series, and then defines the Taylor series of a function at an input zero. The formula for the k-th coefficient is given as the k-th derivative of the function evaluated at zero, divided by k factorial. The professor illustrates this with the example of e^x, showing how its derivatives all evaluate to one, resulting in the familiar series for e^x. The concept is further explored with the sine and cosine functions, highlighting the alternating signs and patterns in their series expansions.
🔍 Applying Taylor Series to Functions
The lecture continues with the application of Taylor series to various functions, starting with the sine function, where the derivatives evaluated at zero lead to alternating zero and non-zero terms, resulting in the series for sine. The cosine function is then examined, with its derivatives following a similar pattern, but yielding a series with only even degree terms and alternating signs. The process is applied to a simple polynomial function, x^3 + 2x^2 - x + 5, to demonstrate the step-by-step calculation of the Taylor series coefficients, leading to a series that matches the original polynomial. The importance of recognizing that polynomials have themselves as their Taylor series is emphasized, connecting to deeper properties of polynomial approximation.
🌀 Exploring the Bessel Function with Taylor Series
The professor introduces the Bessel function j0, which is defined in terms of its Taylor series with complex coefficients. The general form of the Bessel function is discussed, drawing parallels to the cosine function, but with a rapidly increasing denominator in the coefficients. The function's relevance to physical phenomena such as the shape of a rotating chain or the ripples in water when a pebble is dropped is highlighted. The lecture concludes by examining the Taylor series for the Bessel function and its implications for the displacement of a rotating rope, particularly focusing on the linear relationship between the slope at the end of the rope and the square of the angular frequency of rotation.
Mindmap
Keywords
💡Taylor Series
💡e to the x
💡Derivatives
💡Factorial
💡Trigonometric Functions
💡Polynomial
💡Bessel Function
💡Series Expansion
💡Approximation
💡Polynomial Approximation
Highlights
Introduction to lecture three on Taylor series, emphasizing the use of e to the x as a series.
The concept of expressing functions as series with constants and powers of x, with the assumption that every reasonable function can be represented this way.
The critical definition of the Taylor series of a function at an input zero, involving derivatives and factorials.
Application of the Taylor series to the function e to the x, showing how derivatives evaluate to one.
Derivation of the Taylor series for sine and cosine functions, highlighting the alternating signs and patterns in the coefficients.
Explanation of why the Taylor series for cosine function contains only even degree terms.
Application of Taylor series to a simple polynomial function, demonstrating how it simplifies to the original function.
The importance of Taylor series for polynomial approximation and the deep properties it connects to.
The idea of Taylor expansion as an operator that simplifies functions into a long polynomial or series form.
Introduction of the Bessel function j0, defined in terms of its Taylor series, with complex coefficients.
Comparison of the Bessel function j0 to a cosine wave, with a rapidly decreasing amplitude.
Practical application of the Bessel function in describing the shape of a chain or rope when rotated in equilibrium.
Connection between the Bessel function and the rippling effect of waves created by dropping a pebble in water.
Derivation of the displacement of a rope from the vertical axis using the Bessel function and physical constants.
Analysis of the Taylor series for the Bessel function and its implications for the slope at the end of a rotating rope.
The quadratic relationship between the angular frequency and the slope change of a rotating rope.
Conclusion of the lecture with the new definition of Taylor series and its advantages for function expansion.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: