Calculus Chapter 4 Lecture 41 Moments & Gyration

Penn Online Learning

23 Jun 201616:15

EducationalLearning

32 Likes 10 Comments

TLDRIn this calculus lecture, Professor Greist explores moments and gyrations, pivotal concepts in understanding the resistance of solid bodies to rotation. He introduces moments of inertia as a measure analogous to mass for translation, and explains how it can be calculated using integrals for objects with distributed mass. The lecture delves into specific examples, such as calculating the moment of inertia for a disk and a rectangle, and introduces the concept of the radius of gyration, which describes the distribution of mass relative to an axis of rotation. The discussion concludes with the broader implications of these integrals for understanding mass distribution in physical objects.

Takeaways

📚 The lecture introduces the concept of moments and gyrations, focusing on the properties of solid bodies and how integrals can explain these properties.
🔄 Moment of inertia (I) is a measure of resistance to rotation about an axis, similar to how mass is a measure of resistance to translation.
🌀 Moment of inertia can be thought of as the constant of proportionality between torque and angular acceleration, akin to mass's role between force and acceleration.
📏 For a point mass, the moment of inertia is calculated as the square of the distance (R^2) to the axis times the mass (M).
🧩 When dealing with objects with distributed mass, calculus is used to integrate the moment of inertia by dividing the object into differential elements.
⚖️ The moment of inertia of an object is calculated by integrating \( R^2 \, dM \), where \( dM \) is the mass element at a distance R from the axis.
🛷 Understanding moment of inertia is crucial for interpreting physical experiments, such as the speed at which objects roll down an inclined plane and rotate about their axis.
💿 The moment of inertia for a flat disc rotating about its axis is derived, showing the integral simplifies to \( \frac{1}{4} \rho \pi R^4 \), where \( \rho \) is the density and R is the radius.
🎯 The radius of gyration (R_G) is defined as the distance from the axis at which the entire mass of the object would need to be concentrated to have the same moment of inertia.
📐 The radius of gyration is calculated as the square root of the moment of inertia divided by the mass ( \( \sqrt{\frac{I}{M}} \) ), representing the root mean square distance to the axis.
🔢 Higher mass moments, integrals of the form \( x^n \, dM \), provide additional measures of how mass is distributed over an object, with the first mass moment leading to the centroid.

Q & A

What is the moment of inertia and how is it related to physical properties of an object?
-The moment of inertia, denoted by 'I', is a measure of an object's resistance to rotation about an axis. It is analogous to mass, which is a measure of resistance to translation. The moment of inertia can be thought of as the constant of proportionality between torque and angular acceleration.
How does the moment of inertia of a point mass depend on its mass and distance from the axis of rotation?
-For a point mass, the moment of inertia depends on both the mass of the object and the distance 'R' from the axis of rotation. It is given by the formula I = R^2 * M, where 'M' is the mass.
What is the appropriate calculus technique for calculating the moment of inertia of an object with distributed mass?
-To calculate the moment of inertia for an object with distributed mass, the object is divided into differential elements, and the moment of inertia for each element is integrated over the entire mass distribution. The formula for this is I = ∫(R^2 * dM).
How does the mass distribution affect the speed at which an object rotates when rolling down an inclined plane?
-The mass distribution of an object influences its speed when rolling down an inclined plane because it affects the moment of inertia. An object with mass distributed at the outside has a greater moment of inertia and will rotate slower than an object with mass evenly distributed.
What is the formula for calculating the moment of inertia of a flat disk rotating about its axis?
-For a flat disk of radius 'R' rotating about its axis, the moment of inertia is calculated by integrating the mass element 'dM' times the square of the distance 'x' from the axis, multiplied by the density 'ρ', over the area of the disk. The formula simplifies to I = (1/4) * ρ * π * R^4.
How does the moment of inertia differ when a disk is rotated about its center versus its edge?
-When a disk is rotated about its center, the moment of inertia is half of that when rotated about its edge. This is because the moment of inertia about the center is one-half M * R^2, and for rotation about the edge, it is M * R^2.
What is the moment of inertia of a rectangle rotating about its vertical axis?
-For a rectangle of length 'L' and height 'H' rotating about its vertical axis, the moment of inertia is calculated by integrating the square of the distance 'x' from the axis times the density 'ρ' and the height 'H', resulting in I = (1/12) * ρ * H * L^3.
What is the radius of gyration and how does it relate to the moment of inertia?
-The radius of gyration, denoted by 'Rg', is the distance from the axis of rotation where the entire mass of the object would need to be concentrated to have the same moment of inertia as the actual distributed mass. It is calculated as the square root of the moment of inertia divided by the mass (Rg = √(I/M)).
What is the physical significance of the radius of gyration in everyday objects?
-The radius of gyration can be felt when hitting an object with a bat; if you hit it at the right spot (the radius of gyration), it feels right. It helps in understanding how mass is distributed in objects and affects their rotational dynamics.
What are the first and second mass moments, and how do they relate to the physical properties of an object?
-The first mass moment is the integral of 'x * dM' and leads to the centroid of the object when normalized. The second mass moment is the integral of 'x^2 * dM' and leads to the moment of inertia and radius of gyration. Both moments provide insights into how mass is distributed across the object.

Outlines

00:00

📚 Introduction to Moments of Inertia and Calculus

Professor Greist begins Lecture 41 by introducing moments and gyrations, and the concept of centers of mass. He explains moments of inertia as a measure of resistance to rotation, analogous to mass being a measure of resistance to translation. The moment of inertia, denoted as 'I', is the constant of proportionality between torque and angular acceleration. For a point mass, the moment of inertia is calculated as the square of the distance to the axis times the mass. The lecture then transitions into a more complex scenario involving distributed mass, where calculus is used to integrate the moment of inertia over differential elements. The physical understanding of moment of inertia is illustrated through an experiment with differently distributed masses rolling down an inclined plane, showing how mass distribution affects the speed of rotation. The specific case of a disk's moment of inertia is calculated, demonstrating the use of integration and symmetry in physical problems.

05:04

🔍 Calculating Moment of Inertia for Different Shapes

The script continues with a detailed explanation of calculating the moment of inertia for a disk rotated about different axes. A trigonometric substitution is introduced to simplify the integral involved in the calculation, leading to the conclusion that the moment of inertia for a disk rotating about its axis is 1/4 times the product of its density, pi, and the fourth power of its radius. The process is then simplified for rotation about the center, yielding a different moment of inertia value. The concept is further explored by comparing the moments of inertia for a rectangle rotated about vertical and horizontal axes, with the integrals and results for both cases provided. The summary emphasizes the importance of understanding how the shape and mass distribution affect the moment of inertia.

10:04

🌐 Radius of Gyration and Mass Distribution

The third paragraph delves into the concept of the radius of gyration, which is a measure of how mass is distributed in an object and how it relates to the moment of inertia. It is defined as the distance from the axis of rotation where the entire mass of the object would need to be concentrated to have the same moment of inertia. The formula for the radius of gyration is derived, and its physical meaning as the root mean square distance to the axis is explained. The lecture encourages students to consider everyday objects and their mass distribution, highlighting the practical implications of the radius of gyration in various physical scenarios. The paragraph also touches on the broader concept of mass moments and their significance in characterizing mass distribution in objects.

15:06

🎯 Higher Mass Moments and Physical Properties

In the final paragraph, the discussion extends to higher mass moments, which are integrals that provide different physical properties related to mass distribution. The zeroth mass moment, which is simply the mass of the object, is mentioned as a basis for understanding other moments. The paragraph concludes the lecture on solid bodies and their properties as described through integrals, and it teases the next topic of probabilities, suggesting a connection between the current material and upcoming lessons. The summary wraps up the lecture by emphasizing the importance of understanding mass distribution and its effects on physical properties.

Mindmap

Keywords

💡Moments of Inertia

Moments of inertia are a measure of an object's resistance to rotational motion about an axis, analogous to mass being a measure of resistance to translation. In the context of the video, moments of inertia are integral to understanding how objects behave when subjected to rotational forces. For instance, a heavier object or one with mass distributed further from the axis will have a higher moment of inertia, making it more challenging to rotate.

💡Torque

Torque is the rotational equivalent of force and is related to the moment of inertia through the relationship that torque equals the moment of inertia multiplied by angular acceleration. In the script, torque is used to illustrate how the distribution of mass in an object affects its rotational behavior, with objects having mass concentrated at the periphery exhibiting greater resistance to rotation.

💡Angular Acceleration

Angular acceleration is the rate of change of angular velocity, and it is directly related to torque through the moment of inertia. The video script uses angular acceleration to explain how the moment of inertia influences the rate at which an object begins to rotate when a torque is applied.

💡Integrals

Integrals are mathematical tools used to calculate the moment of inertia by summing up infinitesimally small contributions from each part of an object. The script explains that for complex objects with distributed mass, integrals allow us to find the moment of inertia by integrating the squared distance of each mass element from the axis of rotation.

💡Differential Elements

Differential elements, or 'differential masses' in the context of the video, refer to the infinitesimally small pieces of an object used in the integration process to calculate moments of inertia. The script mentions dividing an object into these elements to apply calculus techniques and find the object's moment of inertia.

💡Disk

In the script, a disk (or flat disc) is used as an example to demonstrate the calculation of moment of inertia. The professor explains how to integrate over the disk's area to find the moment of inertia when the disk is rotated about different axes, highlighting the importance of the mass distribution within the object.

💡Radius of Gyration

The radius of gyration is a measure of the distribution of an object's mass relative to the axis of rotation. It is defined as the distance from the axis at which the entire mass of the object would need to be concentrated to have the same moment of inertia. The script uses the radius of gyration to illustrate how different mass distributions affect an object's rotational dynamics.

💡Centroid

The centroid is the point at which the mass of an object is considered to be concentrated for the purpose of calculating its moment of inertia. In the video, the concept of the centroid is related to the first mass moment, which is calculated using an integral of the form x * dm, where dm represents an infinitesimally small mass element.

💡Mass Moments

Mass moments, particularly the second mass moment, are integrals that describe how mass is distributed within an object. The script explains that these moments are crucial for understanding an object's resistance to rotational forces and can be calculated using integrals involving powers of the distance from the axis of rotation.

💡Trigonometric Substitution

Trigonometric substitution is a mathematical technique used to simplify integrals, especially those involving square roots of quadratic expressions. In the script, the professor uses trigonometric substitution to simplify the integral for the moment of inertia of a disk, making it easier to evaluate.

💡Symmetry

Symmetry in the context of the video refers to the geometric property of an object that allows for simplification in calculations due to equal distribution of properties across the object. The script mentions using symmetry to simplify the calculation of the moment of inertia for a disk rotated about its axis by integrating over half the disk and multiplying by two.

Highlights

Introduction to moments and gyrations centers of mass and their significance in understanding the properties of solid bodies.

Explanation of moments of inertia as a measure of resistance to rotation, analogous to mass being a measure of resistance to translation.

The concept of moment of inertia, denoted as 'I', as the constant of proportionality between torque and angular acceleration.

Calculation of moment of inertia for a point mass, which depends on mass and the square of the distance to the axis.

Approach to calculate moment of inertia for objects with distributed mass using calculus and integration.

The physical understanding of moment of inertia and its impact on the speed of rotation for objects rolling down an inclined plane.

Computation of moment of inertia for a disk rotated about the y-axis using integration techniques.

Use of symmetry and trigonometric substitution to simplify the integral for moment of inertia of a disk.

Result of moment of inertia for a disk rotated about the y-axis, expressed in terms of its mass and radius.

Calculation of moment of inertia for a disk rotated about the z-axis, demonstrating the simplicity of the process.

Interpretation of the moment of inertia for a symmetric domain and its relation to the vertical and horizontal axes.

Analysis of moment of inertia for a rectangle rotated about vertical and horizontal axes and the resulting inertia values.

Introduction of the radius of gyration as a measure of how mass is distributed in an object.

Derivation of the formula for the radius of gyration and its physical interpretation.

Explanation of the first and second mass moments and their significance in characterizing mass distribution.

Discussion on higher mass moments and their potential physical properties related to mass distribution.

Conclusion of the lecture on solid bodies through integrals of masses, centers, and moments, with a preview of the next topic on probabilities.

Transcripts

Browse More Related Video

Moment of Inertia | Physics with Professor Matt Anderson | M12-05

More on moment of inertia | Moments, torque, and angular momentum | Physics | Khan Academy

10. Rotations, Part II: Parallel Axis Theorem

Calculus Chapter 4 Lecture 44 Expectation and Variance

AP Physics 1 - Rotational Dynamics

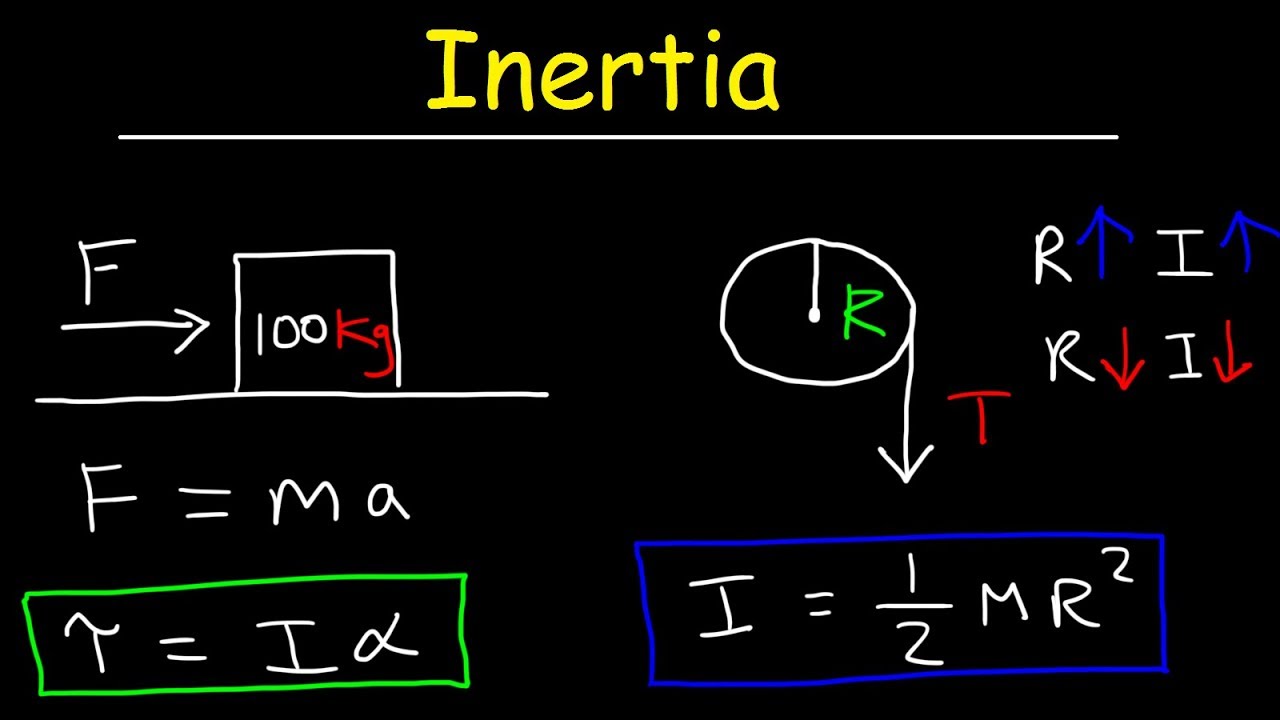
Inertia - Basic Introduction, Torque, Angular Acceleration, Newton's Second Law, Rotational Motion