Calculus Chapter 4 Lecture 39 Averages
TLDRIn this calculus lecture, Professor Greist explores the concept of averaging functions over intervals, emphasizing the importance of interval choice and function variation. He introduces the integral definition of an average function, f-bar, as the constant value where the area above and below the function balance. Examples include calculating the average of monomials, exponentials, and logarithms, as well as applying the concept to physical scenarios like average density and blood flow in vessels. The lecture concludes with the root mean square voltage in AC circuits, illustrating the relevance of different types of averages in various contexts.
Takeaways
- 📊 Averages are intuitive and ubiquitous, often representing a central value.
- 📉 The average of a function over an interval depends on the interval's range.
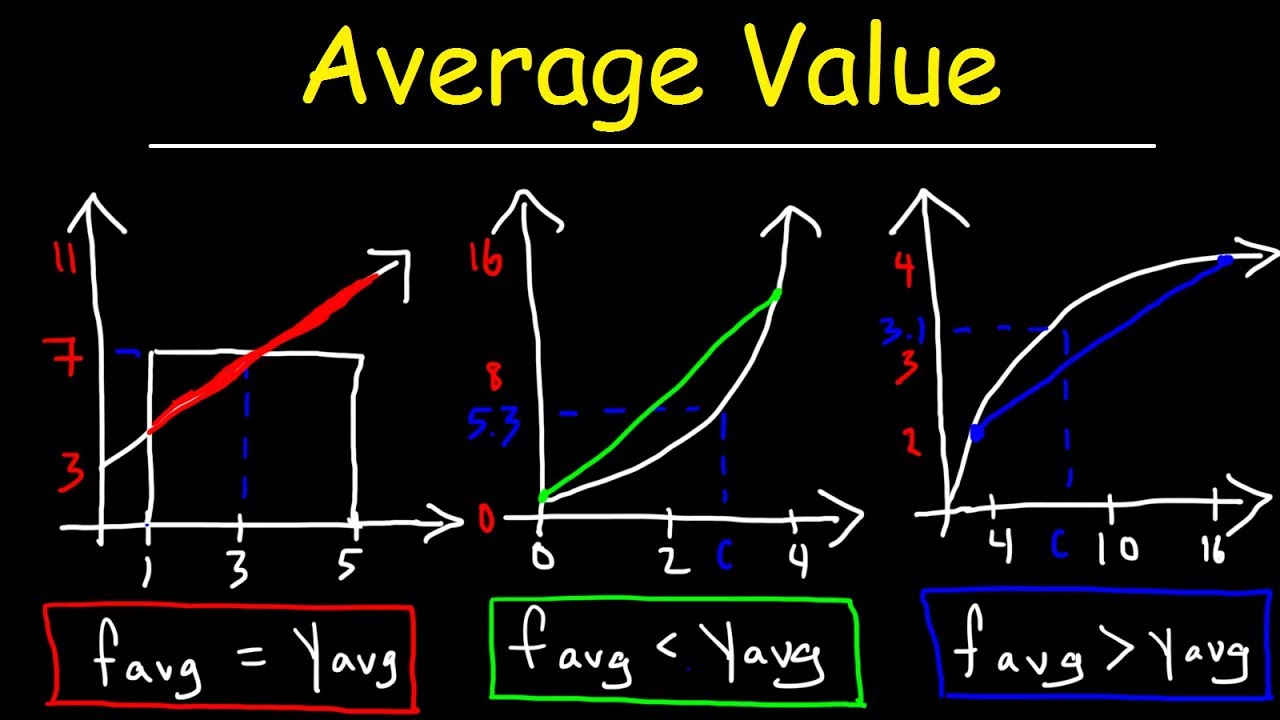
- 📝 The formal definition of an average is the constant value where the areas above and below balance out.
- ➗ The integral form for average is f bar = 1/(B - A) * ∫ from A to B of f(x) dx.
- 📈 This definition is applicable to various domains, including discrete sets and continuous functions.
- 🔢 Examples include calculating the average of polynomials, exponentials, and logarithms over given intervals.
- 🌍 The average density of the Earth is calculated using the volumetric density function and integrating with respect to volume.
- 🩸 For blood flow in a vessel, the average velocity is found by integrating the velocity function with respect to the cross-sectional area.
- ⚡ Alternating current voltage uses the root mean square (RMS) to find an effective average, which accounts for the oscillating nature.
- 📍 Averages can be applied to diverse scenarios like averaging positions, orientations in flocks, or even human faces.
Q & A
What is the definition of an average in the context of a function?
-In the context of a function, the average, denoted by f-bar, is the constant value where the area above and below the function balance out or are equal over a given interval from A to B.
How do you mathematically express the average of a function over an interval?
-The average of a function over an interval can be expressed as the integral of (f(x) - f-bar) dx from A to B, which equals zero. This leads to the formula f-bar = (1/(B-A)) * integral from A to B of f(x) dx.
Why is the integral form of the average function better defined in terms of the ratio of integrals?
-The integral form of the average function is better defined in terms of the ratio of integrals because it allows for an arbitrary integration domain, making it applicable even for discrete sets and not just intervals from A to B.
What is the average value of a monomial function x^n over the interval from 0 to T?
-The average value of x^n over the interval from 0 to T is T^n / (n + 1), which is the function evaluated at the right-hand endpoint divided by n + 1.
How does the average value of an exponential function e^x differ from that of a monomial function?
-The average value of an exponential function e^x over the interval from 0 to T is e^T - 1 divided by T, which is different from the monomial function as it suggests that all the growth happens right at the end of the interval.
What is Pazos' law and how is it used to find the average velocity in a tubular vessel?
-Pazos' law describes the variation of fluid velocity with respect to the radial distance in a cylindrical vessel. It is used to find the average velocity by integrating the velocity function with respect to the area element over the cross-sectional area and then simplifying the result.
What is the root mean square voltage, and why is it used instead of the average voltage for AC circuits?
-The root mean square (RMS) voltage is the square root of the average of the square of the voltage function over a period. It is used instead of the average voltage for AC circuits because the average voltage over a full cycle is zero, which is not useful for practical purposes.
What is the relationship between the RMS voltage and the peak voltage in an AC circuit?
-The RMS voltage is approximately 71% of the peak voltage. This means if a device is labeled as 120 volts RMS, the peak voltage is actually higher, almost 170 volts.
How does the concept of averaging extend beyond numerical values, as mentioned in the script?
-The concept of averaging extends to various domains such as averaging locations or points on a map, orientations or directions in flocking behavior of birds, and even averaging physical attributes like faces using mathematical techniques.
What is the significance of the integral in the context of averaging a collection of locations or positions?
-In the context of averaging a collection of locations or positions, the integral is used to sum up all the individual positions over a domain and then divide by the number of positions to find the average location, which is a more complex application of integration.
Outlines
📊 Introduction to Averages in Calculus
Professor Greist introduces the concept of averages, explaining that an average represents a central value. He emphasizes the importance of the interval over which the average is calculated, using examples like unemployment rates. He then defines the average of a function mathematically as the constant value where the areas above and below balance out. The formula for the average value of a function, f, over an interval [A, B] is introduced, along with the integral definition.
📈 Examples of Calculating Averages
The professor explores specific examples of calculating the average values of functions. He first discusses monomials, showing how to compute the average of x^n over [0, T]. He then moves to exponential functions, demonstrating the average of e^x over the same interval. Finally, logarithms are considered, with a discussion on how the average value of log x over [1, T] shows its slow growth. These examples illustrate the practical computation of average values for different types of functions.
🌍 Calculating Average Density and Blood Flow
This section explores averages in more complex scenarios, starting with the Earth's average density, emphasizing the importance of integrating with respect to volume. The discussion then moves to blood flow through a vessel, using Poiseuille's law to describe how velocity varies with radial distance. The average velocity is calculated using the area element in a cross-sectional view of the vessel, leading to a formula that relates average velocity to the maximal velocity at the vessel's center.
🔋 Root Mean Square and Beyond
The concept of root mean square (RMS) is introduced, particularly in the context of alternating current (AC) voltage. The average voltage over a period is zero, so RMS is used to obtain a meaningful measure. The RMS value of a sinusoidal voltage is derived, showing that it is about 71% of the peak voltage. The discussion then shifts to broader questions, such as averaging positions, orientations in flocks of birds, and even human faces. The professor hints at more advanced topics, suggesting further exploration of the mathematical foundations of averages.
Mindmap
Keywords
💡Average
💡Integral
💡Function
💡Interval
💡Volumetric Density
💡Root Mean Square (RMS)
💡Velocity Profile
💡Poiseuille's Law
💡Exponential Growth
💡Logarithm
Highlights
Introduction to the concept of averages and their mathematical significance.
Discussion on the dependency of averages on the interval of consideration.
Definition of average using integral form: f bar equals 1 over (B - A) times the integral of f from A to B.
Explanation of the improved definition of average in terms of the ratio of integrals.
Application of the average formula to monomials, exponentials, and logarithms.
Calculation of average value of x to the n over an interval.
Calculation of average value of e^x over an interval.
Calculation of average value of log(x) over an interval.
Determining the average density of the Earth using integral formulation.
Introduction to blood flow velocity in a vessel using Poiseuille's law.
Calculation of average velocity of blood flow in a vessel cross-section.
Explanation of root mean square (RMS) and its application to alternating current (AC) voltage.
Derivation of RMS voltage for a sinusoidal function.
Discussion on other types of averages, including averaging locations and orientations.
Preview of the next lesson on averaging collections of locations or positions.
Transcripts
Browse More Related Video

Lec 23 | MIT 18.01 Single Variable Calculus, Fall 2007
Average Value of a Function Over an Interval - Calculus

Calculus Chapter 4 Lecture 40 Centroids & Centers

Math 1325 Lecture 13 3

Calculus: Average Value of a Function (Section 6.5) | Math with Professor V

Lec 21 | MIT 18.01 Single Variable Calculus, Fall 2007
5.0 / 5 (0 votes)
Thanks for rating: