Learn to find the missing angles for a triangle using inverse trig functions
TLDRThe transcript is a detailed explanation of solving a trigonometric problem involving a right triangle. The speaker begins by labeling the triangle, identifying the hypotenuse, opposite side, and adjacent side. They then use the sine function, which relates the opposite side to the hypotenuse, to establish an equation. Recognizing that the angle 'x' is unknown, the speaker introduces the concept of inverse operations, specifically the square root as the inverse of squaring. Applying this to trigonometry, they find the sine inverse to be the solution for the unknown angle. Using a calculator, they demonstrate how to find the sine inverse of the given ratio and obtain the angle 'x'. The process continues with finding angle 'b' by subtracting the found angle 'x' from 180 degrees, as the sum of angles in a triangle equals 180 degrees. The speaker also explores an alternative method to find angle 'b' directly using the cosine function, which relates the adjacent side to the hypotenuse. The summary concludes with the demonstration of using a calculator to find the cosine inverse and solve for angle 'b'. The explanation is designed to be educational, walking the audience through the steps of solving trigonometric problems using inverse trigonometric functions.
Takeaways
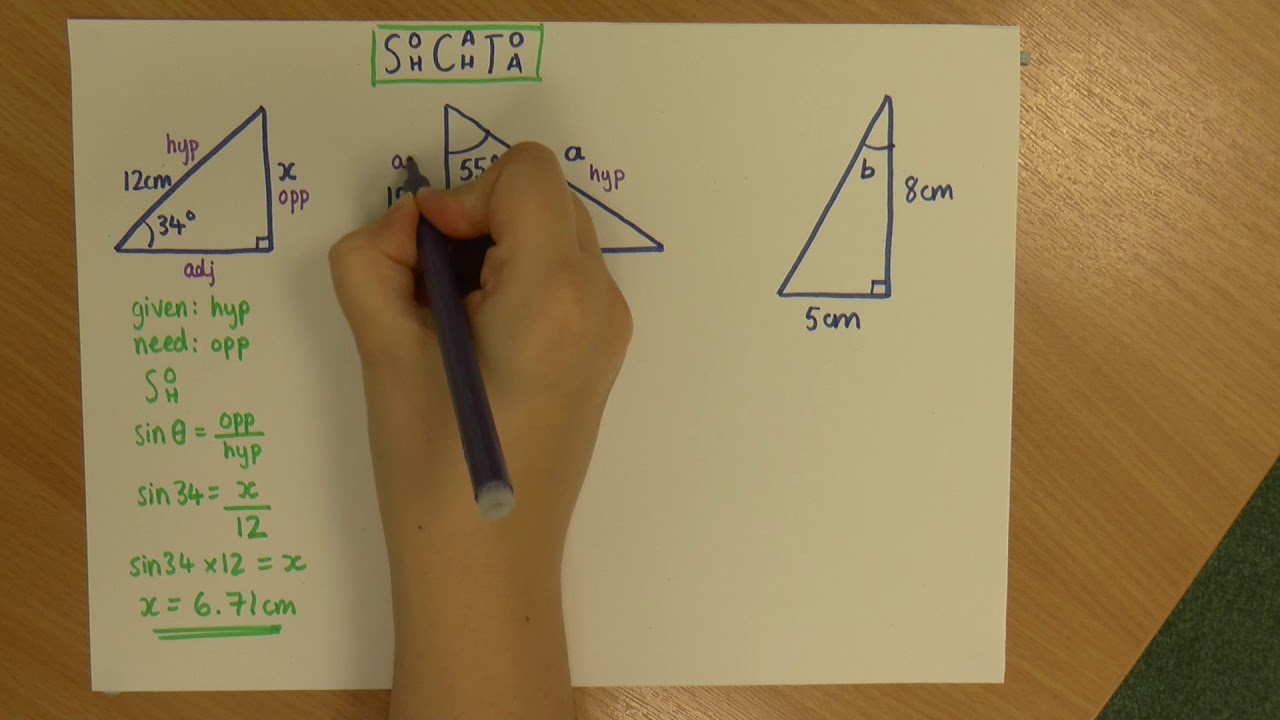
- 📐 **Labeling Triangles**: The first step is to label the sides of the triangle as the hypotenuse, adjacent side, and opposite side relative to the angle in question.
- 📌 **Trigonometric Functions**: The sine function is used to relate the opposite side to the hypotenuse (sin(x) = opposite/hypotenuse).
- 🔍 **Unknown Angles**: When the angle x is unknown, trigonometric functions help establish a relationship between the angle and the sides of the triangle.
- 🧮 **Inverse Operations**: To solve for an unknown, use the inverse operation of the trigonometric function applied. For squaring, it's the square root; for sine, it's the inverse sine (sin^(-1)).
- 🔢 **Calculator Usage**: A scientific calculator is used to find the inverse sine by using the second function button (usually labeled as 'sin^(-1)' or 'inv') above the sine button.
- 📉 **Reducing Fractions**: Before applying trigonometric functions, it's often helpful to reduce fractions to their simplest form.
- 🔄 **Inverse Sine Function**: The inverse sine function is used to find an angle when the ratio of the opposite side to the hypotenuse is known.
- 🤔 **Understanding Inverses**: The concept of inverse operations is crucial for solving trigonometric equations, as it allows for the reversal of the operation that initially created the equation.
- 📐 **Sum of Angles in a Triangle**: The sum of the angles in a triangle always equals 180 degrees, which helps in finding the other angles when one is known.
- 🔁 **Alternative Methods**: There are different ways to approach a problem; for instance, finding angle B directly using the cosine function instead of first finding angle A.
- 📐 **Adjacent and Hypotenuse for Cosine**: When using the cosine function, the adjacent side is divided by the hypotenuse to find the angle.
- 📘 **Final Calculation**: After finding one angle using a trigonometric function, the other angles can be determined by subtracting from 180 degrees, considering the sum of angles in a triangle.
Q & A
What is the first step in solving a triangle when given the lengths of the opposite and hypotenuse sides?
-The first step is to label the triangle, identifying the hypotenuse and distinguishing between the adjacent and opposite sides relative to the angle you are trying to find.
Which trigonometric function is used when you know the lengths of the opposite side and the hypotenuse?
-The sine function is used, as it is defined as the ratio of the length of the opposite side to the length of the hypotenuse.
If you have the equation sine(x) = opposite/hypotenuse and you don't know the angle x, what is the next step?
-The next step is to use the inverse sine function, also known as arcsine, to find the angle x.
What is the inverse operation of squaring a number?
-The inverse operation of squaring a number is taking the square root of that number.
How do you find the angle x using a calculator when you have the sine of the angle?
-You would use the second function (usually labeled as 'sin^-1' or 'arcsin') on your calculator and input the ratio of the opposite side to the hypotenuse.
What mode should your calculator be in when calculating angles in degrees?
-Ensure your calculator is in degree mode to get the correct angle measurement.
If all angles in a triangle add up to a certain total, what is that total?
-All angles in a triangle add up to a total of 180 degrees.
How can you find angle B if you know angle A and the sum of angles in a triangle is 180 degrees?
-You can find angle B by subtracting angle A from 180 degrees.
What is the cosine function used for in a right triangle when you have the lengths of the adjacent side and the hypotenuse?
-The cosine function is used to find the angle when you know the ratio of the adjacent side to the hypotenuse.
How do you find angle B directly without first finding angle A?
-You can use the cosine function, considering the adjacent side over the hypotenuse, and then apply the inverse cosine function to find angle B directly.
What is the relationship between the sine and cosine functions in a right triangle?
-The sine and cosine functions are complementary in a right triangle, meaning that the sine of one acute angle is equal to the cosine of the other acute angle.
Why is it important to understand inverse trigonometric functions when solving for angles in a triangle?
-Inverse trigonometric functions are crucial because they allow you to find the measure of an angle when you know the ratio of the sides of a right triangle, which is often the case in trigonometry problems.
Outlines
📐 Understanding Trigonometry: Sine and Inverse Sine
The first paragraph introduces the concept of labeling a triangle for trigonometric calculations. It explains the process of identifying the hypotenuse, adjacent side, and opposite side in a right triangle. The speaker then uses the sine function, which relates the opposite side to the hypotenuse, to set up an equation. However, since the angle 'x' is unknown, the speaker introduces the concept of inverse operations. Specifically, the inverse operation of squaring is the square root, and similarly, the inverse of the sine function is the sine inverse, denoted as sin^(-1). The speaker demonstrates how to use a calculator to find the sine inverse of a ratio, yielding an angle measurement. The paragraph concludes with a method to find another angle 'b' in the triangle by subtracting the known angles from 180 degrees, the total sum of angles in a triangle.
🔢 Applying Trigonometry: Cosine and Cosine Inverse
The second paragraph expands on the trigonometric functions by introducing cosine and its inverse. The speaker discusses the relationship between the adjacent side and the hypotenuse, which is represented by the cosine function. By setting up the equation with the adjacent side over the hypotenuse, the speaker shows how to use the cosine inverse function to find the angle 'x'. The paragraph demonstrates the process of using a calculator to compute the cosine inverse, which gives the angle measurement for 'x'. Additionally, the speaker provides an alternative method to find angle 'b' directly by using the cosine function and its inverse, avoiding the need to first calculate angle 'x'. The summary emphasizes the use of inverse trigonometric functions to solve for unknown angles in a triangle.
Mindmap
Keywords
💡Triangle
💡Hypotenuse
💡Adjacent Side
💡Opposite Side
💡Trigonometric Function
💡Sine Function
💡Inverse Trigonometric Function
💡Square Root
💡Inverse Operation
💡Scientific Calculator
💡Degrees
💡Angles in a Triangle
Highlights
Labeling a triangle with the hypotenuse, adjacent side, and opposite side is the initial step.
The sine function is used to relate the opposite side to the hypotenuse in a right triangle.
When the angle is unknown, the sine function is expressed as sine of x equals opposite over hypotenuse.
To solve for the angle x, one must use the concept of inverse functions due to the lack of direct values.
The sine inverse function is the opposite operation to the sine function, which is useful when the angle is unknown.
The process of finding the angle involves using a scientific calculator with sine inverse functionality.
To find the angle, input the ratio of the opposite side to the hypotenuse into the sine inverse function.
It's important to ensure the calculator is in the correct mode, such as degree mode, for accurate results.
After finding angle x, one can determine angle b by subtracting x from 180 degrees, since the angles in a triangle sum up to 180 degrees.
An alternative method to find angle b directly is by using the cosine function, which relates the adjacent side to the hypotenuse.
The cosine inverse function is used in a similar manner to the sine inverse to find the unknown angle when only the adjacent and hypotenuse sides are known.
The transcript demonstrates the step-by-step process of using trigonometric functions and inverse operations to solve for angles in a triangle.
Understanding inverse operations is crucial for solving trigonometric problems, especially when direct values are not provided.
The transcript emphasizes the use of a scientific calculator to perform inverse trigonometric functions.
The process of solving for an angle in a triangle using trigonometric functions is made clear through practical examples.
The transcript provides a clear explanation of how to use the sine and cosine inverse functions to find unknown angles in a triangle.
Trigonometric functions are essential tools in solving geometric problems involving right triangles.
The transcript demonstrates the application of trigonometry in a practical, step-by-step manner, making it accessible for learners.
The importance of using the correct inverse operation corresponding to the trigonometric function used is highlighted.
Transcripts
Browse More Related Video
Trigonometry: Finding missing sides and angles

Trig - 0.6 Trig Functions of Acute Angles
Trigonometry - How To Solve Right Triangles

Trigonometry made easy

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)
05 - Sine and Cosine - Definition & Meaning - Part 1 - What is Sin(x) & Cos(x) ?
5.0 / 5 (0 votes)
Thanks for rating: