Trigonometry - Quadrant rule : Solving Sin θ = a positive value : ExamSolutions

ExamSolutions
15 Oct 200810:00
EducationalLearning
32 Likes 10 Comments

TLDRThis tutorial introduces the quadrant method for solving trigonometric equations involving angles with specific sign values. The example demonstrates how to find angles with a sine value of 0.5, by marking positive sine regions in the first and second quadrants and calculating the angles within the 0° to 360° range. The process includes using the inverse sine function to find the 30° angle and then determining the corresponding angles in the second quadrant, resulting in two solutions: 30° and 150°. The video also explains how to approach the problem for angles between -360° and 0°, yielding the solutions of -210° and -330°.

Takeaways
  • 📚 The tutorial is focused on solving trigonometric equations involving the sine of an angle.
  • 📐 The method used is called the 'quadrant method', which was previously discussed in an earlier tutorial.
  • 🔍 The quadrant method involves understanding the signs of trigonometric functions in different quadrants.
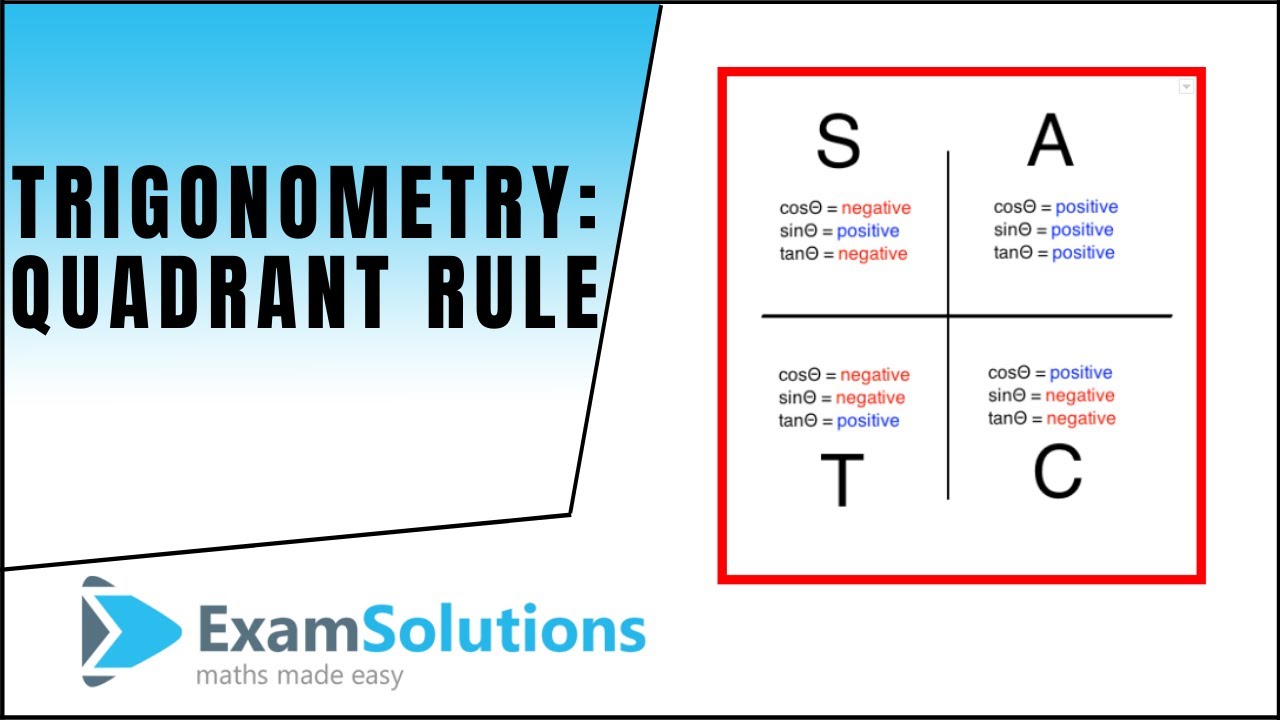
  • 🌐 The sine function is positive in the first and second quadrants, which is crucial for solving the equation.
  • 📈 The tutorial demonstrates how to use the quadrant diagram to determine where the sine function is positive.
  • 📉 The example provided involves finding the angle whose sine is 0.5, and the method involves drawing lines in the first and second quadrants.
  • 🔢 The first solution for the angle is found by taking the inverse sine (arcsin) of 0.5, which equals 30°.
  • 🔄 The second solution is found by subtracting the first solution from 180°, resulting in 150°.
  • 🔠 The tutorial also covers solving for angles in a range of -360° to 0°, which involves a different approach in the quadrant diagram.
  • 🔄 For the negative range, the solutions are found by adding or subtracting 30° from 180° and 360°, resulting in -210° and -330° respectively.
Q & A

  • What is the main topic of this tutorial?

    -The main topic of this tutorial is solving trigonometric equations involving the sign of an angle using the quadrant method.

  • What is the quadrant method?

    -The quadrant method is a technique used to determine the signs of trigonometric functions in different quadrants of the unit circle, which helps in solving trigonometric equations.

  • What is the angle Theta in the context of this tutorial?

    -In this tutorial, angle Theta represents the unknown angle in the trigonometric equation that needs to be solved.

  • What is the value of the sine of angle Theta in the given example?

    -In the given example, the sine of angle Theta is a positive value of 0.5.

  • In which quadrants is the sine function positive?

    -The sine function is positive in the first and second quadrants of the unit circle.

  • How does the tutorial suggest finding the value of Theta?

    -The tutorial suggests finding the value of Theta by using the inverse sine function on a calculator, given that the sine of Theta is 0.5.

  • What is the first value of Theta found in the 0° to 360° range?

    -The first value of Theta found in the 0° to 360° range is 30°, which corresponds to the angle in the first quadrant where sine is positive.

  • How is the second value of Theta calculated?

    -The second value of Theta is calculated by subtracting the first value (30°) from 180°, resulting in 150°, which is the angle in the second quadrant where sine is also positive.

  • What are the two common ranges for solving trigonometric equations as mentioned in the tutorial?

    -The two common ranges for solving trigonometric equations mentioned in the tutorial are 0° to 360° and -360° to 0°.

  • How are the solutions for Theta in the -360° to 0° range determined?

    -The solutions for Theta in the -360° to 0° range are determined by considering the negative angles equivalent to the positive angles found in the 0° to 360° range, such as -210° and -330°.

Outlines
00:00
📚 Introduction to Solving Trigonometric Equations with the Quadrant Method

This paragraph introduces a tutorial on solving trigonometric equations, specifically focusing on the quadrant method. The example given involves an angle, Theta, with a positive sine value of 0.5. The quadrant method is explained as a technique previously discussed, where trigonometric ratios are positive in certain quadrants. The tutorial aims to show how to use this method to solve for angles in specific ranges, starting with the first and second quadrants where sine is positive.

05:03
📐 Applying the Quadrant Method to Find Angles in Given Ranges

The second paragraph delves into applying the quadrant method to find the values of Theta within two specific ranges: 0° to 360° and -360° to 0°. The process involves marking the angle's positive sine value on a quadrant diagram and calculating the angle using the inverse sine function. For the first range, two solutions for Theta are identified: 30° and 150°, which are derived from the inverse sine of 0.5. For the second range, the tutorial explains how to adjust the approach to find negative angles, resulting in solutions of -210° and -330°. The importance of understanding the direction of the turn (clockwise or anticlockwise) and the correct interpretation of the results is emphasized.

Mindmap
Keywords
💡Trigonometric Equation
A trigonometric equation is a mathematical equation that involves trigonometric functions such as sine, cosine, or tangent. In the context of this video, the equation involves the sine of an angle (Theta) being equal to a positive value (0.5). The video's main theme revolves around solving such equations using the quadrant method.
💡Quadrant Method
The quadrant method is a technique used to determine the signs of trigonometric functions based on the quadrant in which an angle lies. The video discusses using this method to solve the trigonometric equation by identifying where the sine function is positive, which helps in finding the possible values of the angle Theta.
💡Angle Theta
Angle Theta is the variable in the trigonometric equation being solved in the video. It represents the angle whose sine is equal to 0.5. The video script uses Theta to illustrate how to find the angle's values in different quadrants, which is crucial for solving the equation.
💡First Quadrant
The first quadrant is one of the four quadrants in a coordinate system where both the x and y coordinates are positive. In the video, the first quadrant is where the sine, cosine, and tangent of an angle are all positive. It is used to determine the possible values of Theta where the sine is positive.
💡Second Quadrant
The second quadrant is another quadrant in a coordinate system where the x coordinate is negative and the y coordinate is positive. In the video, the sine function is also positive in the second quadrant, which is important for finding the values of Theta where the sine is positive.
💡Inverse Sine
The inverse sine, often denoted as arcsin or sin^-1, is a trigonometric function that returns the angle whose sine is a given number. In the video, the inverse sine of 0.5 is used to find the angle Theta, which is crucial for solving the trigonometric equation.
💡Acute Angle
An acute angle is an angle that is less than 90 degrees. In the video, the angle Theta is found to be 30 degrees, which is an acute angle. This is significant as it helps in determining the position of Theta in the first quadrant.
💡Range of Theta
The range of Theta refers to the specific interval within which the angle Theta must lie. The video discusses solving the equation for Theta in the range of 0 to 360 degrees and also for negative values, which is essential for understanding the complete set of solutions.
💡Negative Angle
A negative angle in the video refers to an angle measured in a clockwise direction from the positive x-axis. The video explains how to solve for Theta in a range that includes negative angles, such as from -360 to 0 degrees, which is crucial for finding all possible solutions.
💡Quadrant Diagram
The quadrant diagram is a visual tool used in the video to illustrate the quadrant method. It helps in understanding where the trigonometric functions are positive or negative based on the quadrant in which an angle lies. The diagram is essential for visualizing and solving the trigonometric equation.
Highlights

Introduction to solving trigonometric equations involving the sign of an angle using the quadrant method.

Explanation of the quadrant method, which categorizes trigonometric ratios as positive or negative based on the angle's quadrant.

Demonstration of how sine is positive in the first and second quadrants.

Illustration of marking angles in the first and second quadrants where sine is positive.

Guidance on solving equations for angles with sine values, focusing on the specific range of 0° to 360°.

Process of finding the first value of theta by turning anticlockwise from the starting point.

Use of a calculator to find the inverse sine of 0.5 to determine the angle theta.

Identification of the red and green angles as 30° and 150° within the specified range.

Explanation of how to calculate the green angle by subtracting the red angle from 180°.

Introduction of an alternative range for solving equations, from -360° to 0°.

Description of how to adjust the quadrant diagram for negative angle ranges.

Clarification on starting from the correct direction when solving for negative angles.

Use of the previously calculated 30° angle to find corresponding negative angles.

Calculation of the red angle as -210° by adding 30° to 180° and considering the direction of turn.

Determination of the green angle as -330° by subtracting 30° from 360° and accounting for the clockwise turn.

Final summary of the two solutions for theta within the negative angle range: -210° and -330°.

Conclusion of the tutorial with an encouragement to apply the quadrant method in similar examples.

Transcripts

Browse More Related Video

Trigonometry - Quadrant rule : Solving Sin θ = negative value : ExamSolutions

How to solve trigonometric equations with negative angles

Trigonometry: How to use the ASTC Rule | The Quadrant | CAST

REFERENCE ANGLES || PRE-CALCULUS

Coterminal Angles In Radians & Degrees - Basic Introduction, Trigonometry

How To Solve Trigonometric Equations With Multiple Angles - Trigonometry

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryQuadrant MethodSolve EquationsAngle ThetaPositive ValueSign of AngleFirst QuadrantSecond QuadrantInverse SignTrig RatiosCalculus Tutorial