Trigonometry - Quadrant rule : Solving Sin ΞΈ = negative value : ExamSolutions

ExamSolutions
14 Oct 200810:00
EducationalLearning
32 Likes 10 Comments

TLDRThis tutorial video explains how to solve trigonometric equations using the quadrant method, focusing on the example of sine of an angle theta equaling a negative number minus 0.5. The instructor demonstrates how to determine the sign of trigonometric ratios in different quadrants and how to find the angles that satisfy the equation within specific ranges, such as between 0 and 360 degrees or -180 and 180 degrees. By marking the negative sine quadrants and using inverse sine, the video shows how to identify the correct angles, concluding with the solutions of 210 degrees and 330 degrees for the given range.

Takeaways
  • πŸ“š The tutorial focuses on solving a trigonometric equation using the quadrant method, specifically for the equation sine(theta) = -0.5.
  • πŸ“ The quadrant method is based on understanding where trigonometric functions are positive or negative across different quadrants of the unit circle.
  • πŸŒ€ The sine function is positive in the first and second quadrants and negative in the third and fourth quadrants, which is crucial for solving the equation.
  • πŸ“ˆ The tutorial demonstrates how to mark the unit circle with lines representing where sine is negative, focusing on the third and fourth quadrants.
  • πŸ” The process involves finding the angle whose sine is -0.5 by taking the inverse sine (arcsin) of -0.5, which yields an angle of -30 degrees.
  • πŸ”„ The negative angle indicates a clockwise rotation, which is important for understanding the direction of the angle in the context of the unit circle.
  • πŸ“‰ The magnitude of the angle is 30 degrees, despite the negative sign, which helps in determining the positions of the angles on the unit circle.
  • πŸ“ Two angles are identified as solutions within the range of 0 to 360 degrees: 210 degrees and 330 degrees.
  • πŸ”„ For a different range, such as -180 to 180 degrees, the process involves considering negative angles and clockwise rotation to find the solutions.
  • πŸ“ The tutorial explains how to establish the angles for the negative range by using the inverse sine of -0.5 and adjusting for the direction of rotation.
  • πŸ”‘ The solutions for the range of -180 to 180 degrees are -150 degrees and -30 degrees, which are derived from understanding the rotation in the negative sense.
Q & A

  • What is the trigonometric equation being discussed in the tutorial?

    -The tutorial discusses the equation sine of an angle theta equals a negative number minus 0.5.

  • What method is used in the tutorial to solve the trigonometric equation?

    -The method used in the tutorial is called the quadrant method.

  • How do trigonometric ratios vary between 0 and 90 degrees?

    -Between 0 and 90 degrees, all trigonometric ratios (sine, cosine, and tangent) are positive.

  • What is the sign of the sine function between 90 and 180 degrees?

    -Between 90 and 180 degrees, only the sine function is positive.

  • Which trigonometric ratio is positive between 180 and 270 degrees?

    -Between 180 and 270 degrees, only the tangent ratio (tan) is positive.

  • What trigonometric ratio is positive between 270 and 360 degrees?

    -Between 270 and 360 degrees, only the cosine ratio (cos) is positive.

  • In which quadrants is the sine function negative?

    -The sine function is negative in the third and fourth quadrants.

  • How does the tutorial suggest marking the angles for the sine function being negative?

    -The tutorial suggests marking two lines in the third and fourth quadrants, ensuring they are equally inclined to the horizontal line.

  • What is the common range for solving trigonometric equations in the tutorial?

    -The common range for solving trigonometric equations in the tutorial is from 0 degrees to 360 degrees.

  • How does the tutorial handle the negative angle in the equation?

    -The tutorial explains that a negative angle indicates turning in the clockwise direction, and it uses the inverse sine of -0.5 to find the angle.

  • What are the solutions for theta in the range from 0 to 360 degrees?

    -The solutions for theta in the range from 0 to 360 degrees are 210 degrees and 330 degrees.

  • What happens if the range for theta is from -180 to 180 degrees?

    -If the range for theta is from -180 to 180 degrees, the solutions would be -150 degrees and -30 degrees.

Outlines
00:00
πŸ“š Introduction to Solving Trigonometric Equations

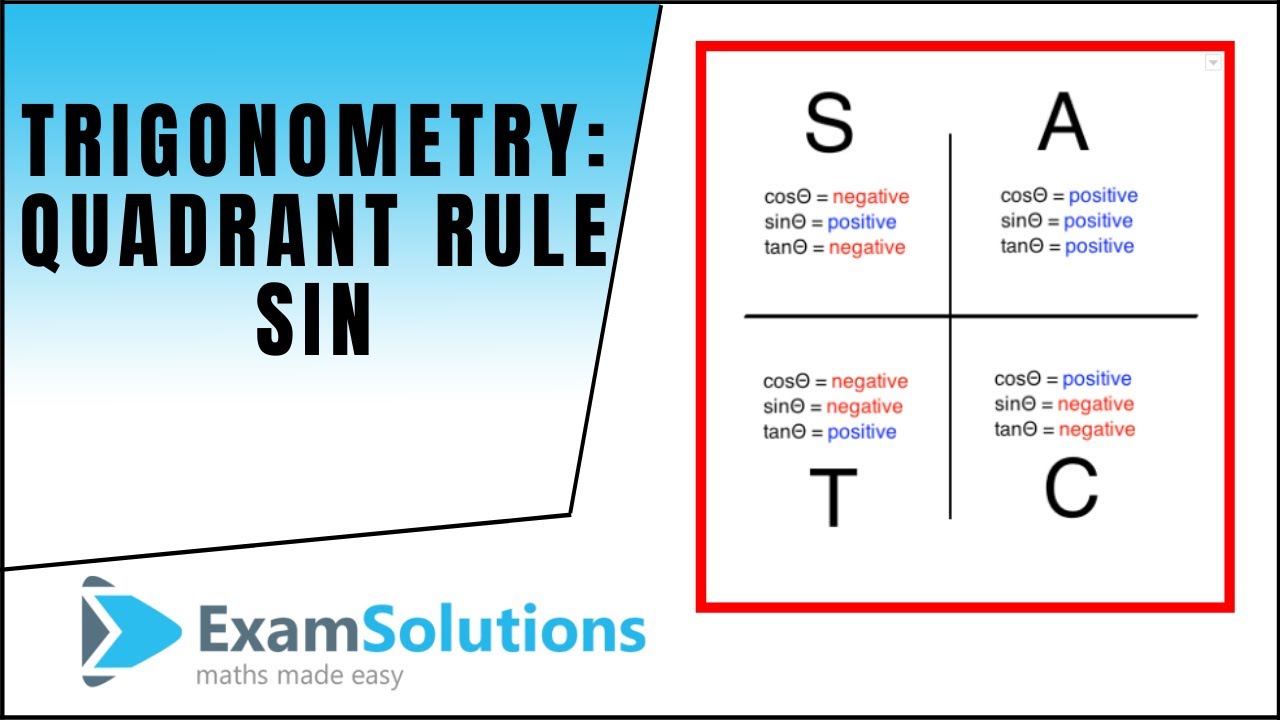
This paragraph introduces a tutorial on solving trigonometric equations, specifically focusing on an equation involving the sine function set equal to a negative number. The method to be used is the quadrant method, which relies on understanding the sign of trigonometric ratios in different quadrants. The tutorial begins by reviewing how sine, cosine, and tangent behave in the four quadrants of the unit circle, emphasizing that sine is positive in the first and second quadrants, tangent in the third, and cosine in the fourth. The process then involves identifying the quadrants where sine is negative, which are the third and fourth, and using this information to set up the problem for solving within a given range of angles, typically from 0 to 360 degrees.

05:02
πŸ” Detailed Explanation of the Quadrant Method

The second paragraph delves deeper into the quadrant method by illustrating how to solve for angles where sine is negative. The tutorial marks two lines in the third and fourth quadrants to represent angles with negative sine values. It explains the process of finding the values of theta within a given range, which is often from 0 to 360 degrees. The method involves starting from the 0-degree line and turning anti-clockwise to the first line, marking a possible theta value, and then continuing to the second line for another theta value. The tutorial uses the example of finding theta by taking the inverse sine of -0.5, which yields an angle of -30 degrees. It clarifies that -30 degrees indicates a clockwise turn from the positive x-axis, leading to the identification of two specific angles, 210 degrees and 330 degrees, as solutions within the specified range. The paragraph also discusses an alternative range for theta, from -180 to 180 degrees, and how to adjust the method accordingly to find the correct angles in this scenario, resulting in solutions of -150 degrees and 150 degrees.

Mindmap
Keywords
πŸ’‘Trig Equation
A trig equation is a mathematical equation that involves trigonometric functions such as sine, cosine, or tangent. In the video, the trig equation is specifically about finding the angle where sine of the angle equals a negative number. The method used to solve this equation is central to the video's theme, illustrating how to determine the angle values based on the quadrant in which the sine function is negative.
πŸ’‘Quadrant Method
The quadrant method is a technique used to solve trigonometric equations by determining the quadrants in which the trigonometric function has a specific sign. In the video, this method is used to find the angles where the sine function is negative, which are in the third and fourth quadrants. This method is crucial for solving the given trig equation and understanding the behavior of trigonometric functions in different quadrants.
πŸ’‘Trigonometric Ratios
Trigonometric ratios, such as sine, cosine, and tangent, are fundamental in trigonometry and are used to relate the angles of a triangle to the lengths of its sides. In the video, the behavior of these ratios in different quadrants is discussed, highlighting that sine is positive in the first and second quadrants and negative in the third and fourth quadrants, which is essential for solving the trig equation.
πŸ’‘Sine Function
The sine function is a trigonometric function that relates the ratio of the opposite side to the hypotenuse in a right-angled triangle. In the video, the sine function is used to set up the equation sine(theta) = -0.5, where theta is the angle being solved for. The sine function's negativity in certain quadrants is a key aspect of the video's narrative.
πŸ’‘Inverse Sine
The inverse sine, often denoted as arcsin or sin^-1, is a function that returns the angle whose sine is a given number. In the video, the inverse sine is used to find the angle corresponding to a sine value of -0.5, which is crucial for determining the angle values in the trig equation. The result of this calculation is an angle of -30 degrees, which is then used to find other angles in the problem.
πŸ’‘Quadrants
Quadrants in trigonometry refer to the four equal divisions of the coordinate plane formed by the intersection of the x-axis and y-axis. The video discusses how trigonometric functions behave differently in each quadrant, specifically noting that sine is negative in the third and fourth quadrants. Understanding these quadrants is essential for solving the trig equation and determining the correct angles.
πŸ’‘Angles
In the context of the video, angles are the measures of rotation from a reference direction, typically the positive x-axis. The video focuses on finding specific angles, such as theta, where the sine function equals a negative number. The angles derived from the inverse sine function and their relationships to the quadrants are central to solving the trig equation.
πŸ’‘Range of Theta
The range of theta refers to the set of values that the angle theta can take within a given problem. In the video, two common ranges are discussed: from 0 to 360 degrees and from -180 to 180 degrees. These ranges are crucial for determining the valid solutions to the trig equation, as they define the domain in which the angle values must fall.
πŸ’‘Clockwise and Anti-Clockwise
Clockwise and anti-clockwise are terms used to describe the direction of rotation around a point. In the video, these terms are used to explain how angles are measured and how they relate to the sine function's negativity. The video clarifies that a negative angle indicates a clockwise rotation, which is important for understanding the angles derived from the inverse sine function.
πŸ’‘Degrees
Degrees are a unit of measurement used to quantify angles. In the video, degrees are used to express the angles derived from the trig equation and the inverse sine function. The discussion of degrees, such as -30 degrees and 30 degrees, is essential for understanding the specific angles that satisfy the sine equation in the given ranges.
Highlights

Introduction to solving a trigonometric equation using the quadrant method.

Explanation of how trigonometric ratios vary in sign between different quadrants.

Sine is positive in the first and second quadrants and negative in the third and fourth.

Demonstration of how to mark quadrants where sine is negative for solving the equation.

The process of eliminating quadrants where sine is positive from the solution set.

Marking two lines in the third and fourth quadrants to represent the negative sine values.

Ensuring the lines are equally inclined to the horizontal to represent the same angle size.

Solving for theta within the range of 0 to 360 degrees as a common approach.

Starting the solution from the 0-degree line and turning anti-clockwise to find possible theta values.

Using the inverse sine function to find the angle corresponding to -0.5.

Calculating the angle of -30 degrees and its relation to the clockwise direction.

Determining the magnitude of the angle as 30 degrees despite the negative sign.

Establishing the red angle as a turn of 180 degrees plus an additional 30 degrees.

Calculating the green angle as a turn of 360 degrees minus 30 degrees.

Identifying the solutions to the equation within the given range as 210 degrees and 330 degrees.

Exploring an alternative range for theta between -180 degrees and 180 degrees.

Adjusting the solution approach for negative angles and turning in the clockwise direction.

Finding the two solutions for theta within the negative range as -150 degrees and -30 degrees.

Transcripts

Browse More Related Video

Trigonometry - Quadrant rule : Solving Sin ΞΈ = a positive value : ExamSolutions

How to solve trigonometric equations with negative angles

REFERENCE ANGLES || PRE-CALCULUS

Trigonometry: How to use the ASTC Rule | The Quadrant | CAST

How To Evaluate Trigonometric Functions Using Periodic Properties - Trigonometry

Even and Odd Trigonometric Functions & Identities - Evaluating Sine, Cosine, & Tangent

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometrySine FunctionQuadrant MethodTrig EquationsMath TutorialSolving AnglesInverse SineTrig RatiosMath EducationEducational Content