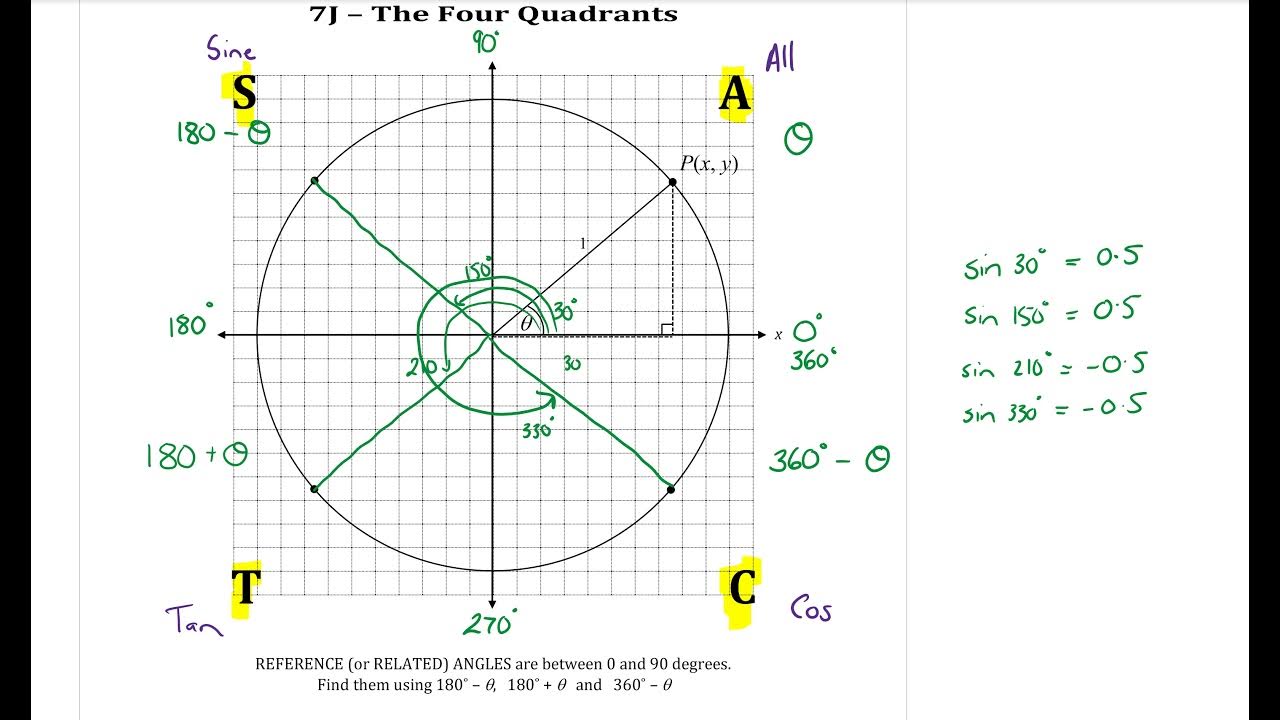
The Signs of Trigonometric Functions(All Students Take Calculus)
TLDRThe video script discusses the signs of trigonometric functions across different quadrants. It explains that in the first quadrant, all trig functions are positive, while in the second and third quadrants, only certain functions maintain their positivity. The mnemonic 'all students take calculus' is used to remember the signs, with each word representing a quadrant and the initial letter corresponding to the sign of the trig functions. The video also provides a method to solve problems by identifying the quadrant based on the signs of sine and secant.
Takeaways
- 📈 In the first quadrant, all trigonometric functions (sine, cosine, and tangent) are positive.
- 📌 Sine (sin(θ)) represents the y-coordinate over the hypotenuse (R), cosine (cos(θ)) is the x-coordinate over R, and tangent (tan(θ)) is y/x.
- 🔄 The signs of the trig functions change with each quadrant: positive in Q1, negative x in Q2, negative y in Q3, and positive x and y in Q4.
- 💡 The mnemonic 'all students take calculus' is used to remember the signs of the trig functions in each quadrant.
- 📊 In the second quadrant, cosine is negative and sine is positive, leading to a negative tangent.
- 📐 In the third quadrant, both sine and cosine are negative, but tangent is positive because it's the division of two negatives.
- 🌟 In the fourth quadrant, only cosine is positive, while sine and tangent are negative, reinforcing the mnemonic's reference to 'calculus'.
- 🤓 The mnemonic 'all students take calculus' can be visualized as 'all' for sine, 'students' for tangent, and 'calculus' for cosine, which correspond to the first letters of 'A', 'S', and 'C'.
- 🔑 To find the quadrant for a given trig function value, use the mnemonic and the signs of the functions to deduce the correct quadrant.
- 📚 The video provides an example of using the mnemonic to determine the quadrant where sine is negative and secant (the reciprocal of cosine) is positive, which is the fourth quadrant.
Q & A
What are the main topics discussed in the video?
-The main topics discussed in the video are the signs of trigonometric functions and how to remember them across different quadrants of the Cartesian coordinate system.
How are trigonometric functions positive in the first quadrant?
-In the first quadrant, all trigonometric functions are positive because both the x and y coordinates (R) are positive, resulting in positive values for sine (θ), cosine (θ), and tangent (θ).
What is the relationship between sine, cosine, and the coordinates in the first quadrant?
-In the first quadrant, sine (θ) is represented as y/R, cosine (θ) as x/R, and tangent (θ) as y/x. Since both x and y are positive, all these functions are positive.
How does the sign of trigonometric functions change in the second quadrant?
-In the second quadrant, cosine (θ) is negative because x is negative, while sine (θ) remains positive as y is positive. Tangent (θ) becomes negative because it involves dividing a positive by a negative.
What are the mnemonics provided in the video to remember the signs of trigonometric functions?
-The video provides a mnemonic: 'all students take calculus' to remember that in the first quadrant, all trigonometric functions (sine, cosine, tangent) are positive.
How does the sign of cosine differ between the first and second quadrants?
-Cosine is positive in the first quadrant but becomes negative in the second quadrant due to the negative x-coordinate.
What is the significance of the quadrant where sine is negative and secant is positive?
-The quadrant where sine is negative and secant (the reciprocal of cosine) is positive is the fourth quadrant, as it implies that cosine is positive and sine is negative.
How does the video use humor to help memorize the signs of trigonometric functions?
-The video uses a play on words with 'all students take calculus' as a humorous way to remember that in the first quadrant, all trigonometric functions are positive.
What is the relationship between the signs of the trigonometric functions and the signs of their reciprocals (cosecant, secant, and cotangent)?
-The signs of the reciprocals (cosecant, secant, and cotangent) are the same as the signs of the original trigonometric functions (sine, cosine, tangent) in the first quadrant.
How does the sign of tangent change in the third quadrant?
-In the third quadrant, tangent (θ) is positive because it involves dividing a negative y by a negative x, which results in a positive value.
What is the method to find the quadrant where sine of theta is less than zero and secant of theta is greater than zero?
-To find the quadrant where sine of theta is less than zero and secant of theta is greater than zero, you look for the quadrant where cosine (and thus secant, as secant is the reciprocal of cosine) is positive and sine is negative, which is the fourth quadrant.
Outlines
📚 Introduction to Trigonometric Functions' Signs
This paragraph introduces the concept of signs of trigonometric functions, specifically in the context of the four quadrants of the Cartesian coordinate system. It explains that in the first quadrant, all trigonometric functions (sine, cosine, and tangent) are positive because both x and y coordinates are positive. The explanation includes a brief review of the definitions of sine, cosine, and tangent in terms of the coordinates (x, y) and the radius R from the origin. The paragraph also introduces a mnemonic device, 'all students take calculus,' to help remember the signs of the trigonometric functions and their reciprocals (cosecant, secant, and cotangent) across the different quadrants.
Mindmap
Keywords
💡Trigonometric Functions
💡Signs of Trig Functions
💡Quadrants
💡Reciprocals of Trig Functions
💡Positive and Negative Values
💡Right Triangle
💡Cartesian Coordinate System
💡Sine (sin)
💡Cosine (cos)
💡Tangent (tan)
💡Mnemonic
Highlights
Introduction to the signs of trigonometric functions
All trig functions are positive in the first quadrant (Quadrant 1)
In Quadrant 1, sine (θ) is Y/R, cosine (θ) is X/R, and tangent (θ) is Y/X
Explanation of why all trig functions are positive in Quadrant 1
Reciprocals of trig functions: cosecant, secant, and cotangent
Signs of trig functions in Quadrant 2: cosine is negative, sine is positive
Signs of trig functions in Quadrant 3: sine is negative, cosine is negative, tangent is positive
Signs of trig functions in Quadrant 4: cosine is positive, sine is negative, tangent is negative
Mnemonic for remembering signs: 'All students take calculus'
Example problem: finding the quadrant where sine is less than zero and secant is greater than zero
Solution to the example problem: Quadrant 4
Explanation of how the mnemonic helps in solving the problem
The importance of understanding the signs of trig functions in solving problems
The video provides a method to remember the signs of trig functions across different quadrants
The use of a simple mnemonic to aid in memorization and quick recall of trig function signs
The video's approach to teaching trigonometry is tailored to students taking calculus
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: