Arc Length (formula explained)
TLDRThis script explains the concept of calculating the arc length of a curve using calculus. It introduces the idea of approximating the curve with small straight segments and then summing these to find the total length. The video demonstrates two methods: one where y is a function of x, and another where x is a function of y. It uses the Pythagorean theorem to derive the formulas for arc length and emphasizes the importance of differentiation in finding the necessary derivatives.
Takeaways
- 📐 The script discusses how to calculate the length of a curve using calculus.
- 📈 It suggests using the concept of a tangent line to a curve to approximate the curve's length.
- 📍 The script introduces the idea of taking a small segment of the curve and using the Pythagorean theorem to estimate its length.
- 🔍 It explains that as the segment becomes smaller, the approximation becomes more accurate.
- 📏 The script uses the notation \( \Delta L \) to represent the small length of the curve being approximated.
- 📚 It mentions that the length of the curve can be found by summing up all the small \( \Delta L \) segments, which is essentially an integration process.
- 📘 The script differentiates between two scenarios: when y is a function of x and when x is a function of y, each requiring a different approach to calculate the arc length.
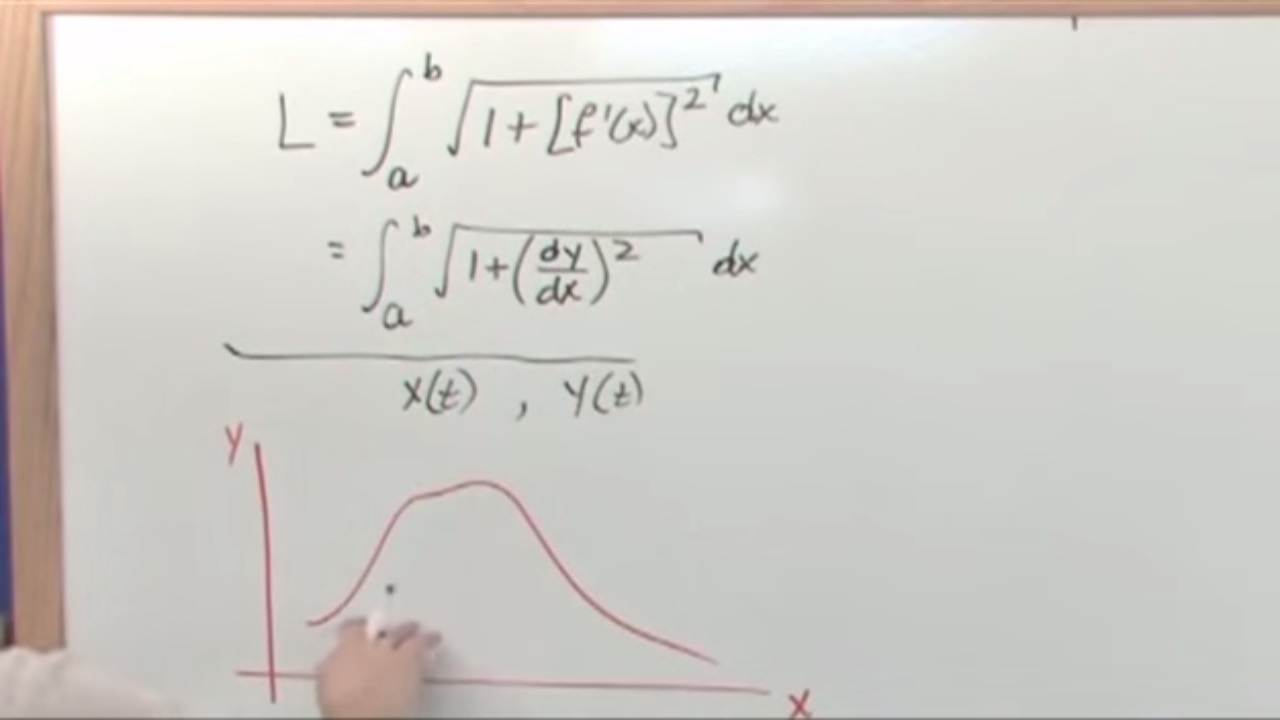
- 🔢 For y as a function of x, the script provides the formula for arc length as the integral of the square root of \( 1 + \left(\frac{dy}{dx}\right)^2 \) with respect to x.
- 🔡 For x as a function of y, the formula involves the integral of the square root of \( 1 + \left(\frac{dx}{dy}\right)^2 \) with respect to y.
- 📉 The script emphasizes the importance of derivatives in calculating the arc length, as they are used to find the rate of change of y with respect to x or x with respect to y.
- 📝 It concludes by encouraging viewers to ask questions if they have any, indicating an open invitation for further clarification.
Q & A
What is the main topic of the video script?
-The main topic of the video script is calculating the length of a curve using calculus and the concept of infinitesimally small tangent lines.
Why can't we simply measure the length of a curve directly?
-We can't measure the length of a curve directly because it is not a straight line; it requires more complex methods involving calculus to approximate and calculate the length accurately.
What is the role of a tangent line in calculating the length of a curve?
-A tangent line is used to approximate a small segment of the curve. By summing up these small tangent segments, we can approximate the total length of the curve.
How is the Pythagorean theorem applied in this context?
-The Pythagorean theorem is applied to calculate the length of an infinitesimally small segment of the curve, which forms a right triangle with the changes in x (dx) and y (dy) values.
What is the formula for the infinitesimal length (dL) of the curve segment?
-The formula for the infinitesimal length (dL) of the curve segment is \( dL = \sqrt{dx^2 + dy^2} \).
How do we integrate to find the total arc length of the curve?
-To find the total arc length of the curve, we integrate the infinitesimal lengths (dL) along the interval of interest, which involves integrating \( \sqrt{1 + (dy/dx)^2} \) or \( \sqrt{1 + (dx/dy)^2} \) depending on whether y is a function of x or x is a function of y.
What adjustments are made when the curve is defined as y = f(x)?
-When the curve is defined as y = f(x), we use the integral \( \int_{a}^{b} \sqrt{1 + \left( \frac{dy}{dx} \right)^2} \, dx \), where the derivative dy/dx is squared and added to 1 inside the square root.
What changes when the curve is defined as x = g(y)?
-When the curve is defined as x = g(y), we use the integral \( \int_{c}^{d} \sqrt{1 + \left( \frac{dx}{dy} \right)^2} \, dy \), where the derivative dx/dy is squared and added to 1 inside the square root.
Why is it necessary to factor out dx^2 or dy^2 in the integral expressions?
-Factoring out dx^2 or dy^2 simplifies the expression under the square root, allowing us to separate the differential element (dx or dy) and integrate more easily.
What are the limits of integration in the arc length formula?
-The limits of integration depend on the interval over which we are measuring the curve. For y = f(x), the limits are from x = a to x = b. For x = g(y), the limits are from y = c to y = d.
Outlines
📐 Calculating Arc Length Using Tangent Approximations
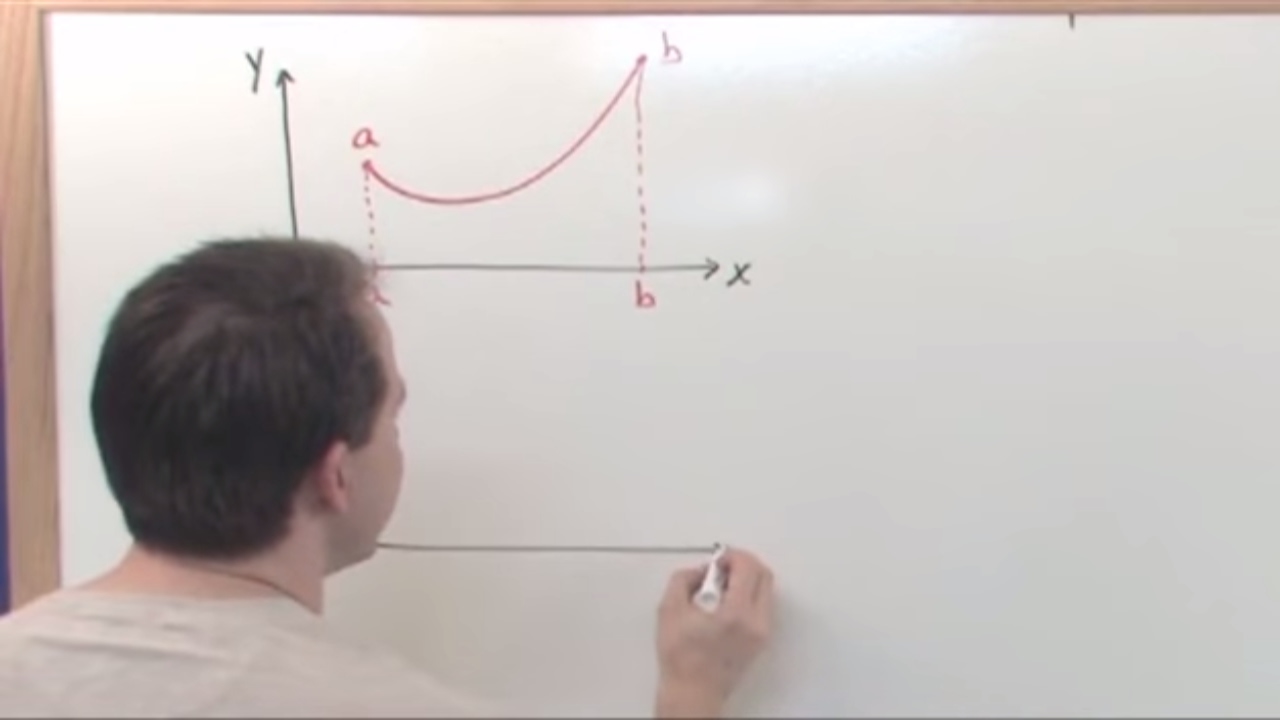
The first paragraph introduces the concept of finding the length of a curve using calculus. It explains the process of approximating the curve with small straight segments (tangents) and summing their lengths to estimate the total arc length. The explanation includes placing a tangent line at a chosen point on the curve, using the Pythagorean theorem to relate the small changes in x (dx) and y (dy) values to the length of the tangent segment (DL). The paragraph also discusses the algebraic manipulation needed to express DL in terms of dx and dy, and how integration is used to find the total arc length, with the specific formula depending on whether y is a function of x or vice versa.
📘 Deriving Arc Length Formulas for Different Functions
The second paragraph delves into the specifics of deriving the arc length formulas for two different scenarios: when y is a function of x and when x is a function of y. For y as a function of x, the paragraph explains how to differentiate y with respect to x, square the result, add 1, and then take the square root to find the integrand for the arc length integral. Conversely, when x is a function of y, the process involves differentiating x with respect to y and following a similar procedure. The paragraph concludes by emphasizing the importance of knowing the limits of integration, which are the values of y (or x, depending on the function) over which the curve extends, to calculate the exact arc length.
Mindmap
Keywords
💡Arc length
💡Tangent line
💡Derivative
💡Integration
💡Pythagorean theorem
💡dx and dy
💡Square root
💡Differentiation
💡Y as a function of X
💡X as a function of Y
💡Arc length formula
Highlights
Introduction to the concept of finding the length of a curve using calculus.
Explanation of using a tangent line to approximate the curve for small segments.
Demonstration of how to place a tangent line on a curve for calculation.
Use of the Pythagorean theorem to calculate the length of small segments of the curve.
Introduction of the notation DL for the length of an infinitesimal arc.
Description of adding up all infinitesimal lengths DL to get the total arc length.
Differentiation between the curve defined by Y as a function of X and X as a function of Y.
Derivation of the arc length formula when Y is a function of X using differentiation.
Explanation of factoring out DX squared from the arc length formula.
Derivation of the integrand for the arc length formula involving dy/dx.
Presentation of the final arc length formula for Y as a function of X.
Transition to the scenario where X is a function of Y for finding arc length.
Derivation of the arc length formula when X is a function of Y, including differentiation.
Explanation of factoring out DY squared from the arc length formula in the X as a function of Y scenario.
Final presentation of the arc length formula for X as a function of Y.
Emphasis on the importance of knowing the limits of integration for calculating arc length.
Encouragement for viewers to ask questions for further clarification.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: