Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

Math and Science
18 Aug 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThis advanced calculus tutorial focuses on the concept of arc length in parametric equations. The instructor begins by reviewing the arc length formula in Cartesian coordinates, which involves integrating the square root of 1 plus the derivative of the function squared. The lesson then transitions to finding an equivalent expression for arc length when the function is defined by parametric equations, X(T) and Y(T), instead of the traditional f(x). The process involves comparing two points on the curve, P and P_i-1, to derive the formula for arc length in parametric form, emphasizing the application of calculus concepts to more complex systems.

Takeaways
  • 📚 The video is part of an advanced calculus tutorial focusing on arc length and parametric coordinates.
  • 🔍 The presenter encourages viewers to review previous sections on arc length and surface area for a comprehensive understanding.
  • 📈 The arc length was previously discussed in the context of integration to find the length of a function.
  • 📐 The surface area of a function rotated around the x-axis was also covered, which involved arc lengths.
  • 🌐 The tutorial then transitioned to explaining how to write functions in terms of parametric equations, where x and y are expressed as functions of a third variable, typically denoted as 'T'.
  • 🔑 The current section mirrors the previous arc length section but applies it to parametric equations, where the function is not given as f(x) but as x(T) and y(T).
  • 📝 The arc length formula in Cartesian coordinates is given as an integral from A to B of the square root of 1 plus the derivative of f(x) squared, dx.
  • 🔄 The goal is to find an equivalent expression for arc length when the function is defined in terms of parametric equations x(T) and y(T).
  • 📈 The process involves looking at two points, P and P_i-1, to derive the arc length formula for parametric equations, similar to the method used for Cartesian coordinates.
  • 📚 The presenter suggests going back to the previous section on arc length to understand the process, which will be applied in the same way for parametric equations.
Q & A

  • What is the main topic of this calculus tutorial section?

    -The main topic of this calculus tutorial section is arc length and parametric coordinates, specifically how to calculate arc length using parametric equations.

  • What was the previous topic discussed in the tutorial series?

    -The previous topic discussed in the tutorial series was writing functions in terms of parametric equations.

  • What is a parametric equation?

    -A parametric equation is an equation that expresses the variables of a function in terms of a third variable, usually denoted as 't' for time, separately for x and y coordinates.

  • What is the purpose of the arc length formula in Cartesian coordinates?

    -The arc length formula in Cartesian coordinates is used to calculate the length of a curve defined by a function 'f(x)' by integrating the square root of '1 + (f'(x))^2' from 'a' to 'b'.

  • How does the arc length formula differ when dealing with parametric equations?

    -In parametric equations, the arc length formula differs in that instead of using 'f(x)', you use 'x(t)' and 'y(t)' to find the derivative 'dx/dt' and 'dy/dt', and integrate the square root of '1 + (dx/dt)^2 + (dy/dt)^2'.

  • What is the integral expression for arc length in terms of parametric equations?

    -The integral expression for arc length in terms of parametric equations is the integral from 'a' to 'b' of the square root of '1 + (dx/dt)^2 + (dy/dt)^2' with respect to 't'.

  • Why is it necessary to consider two points when finding the arc length of a curve?

    -It is necessary to consider two points when finding the arc length of a curve to establish a segment of the curve over which the length is to be calculated, allowing for the application of the arc length formula.

  • What is the significance of the points P and P_sub_I_minus_one in the context of this tutorial?

    -The points P and P_sub_I_minus_one represent two consecutive points along the curve in parametric form, which are used to illustrate the process of calculating the arc length between them.

  • How does the process of finding arc length in parametric equations relate to the process in Cartesian coordinates?

    -The process of finding arc length in parametric equations is conceptually similar to that in Cartesian coordinates, with the main difference being the substitution of 'x(t)' and 'y(t)' for 'f(x)' and the calculation of derivatives with respect to the parameter 't'.

  • What is the role of the derivative in calculating the arc length of a curve?

    -The derivative plays a crucial role in calculating the arc length of a curve as it provides the slope of the tangent to the curve at any given point, which is then used in the arc length formula to determine the length of the curve segment.

  • Can the arc length formula be applied to any curve, or are there any restrictions?

    -The arc length formula can be applied to any continuous and differentiable curve. The curve must have a well-defined derivative, which represents the slope of the tangent line at each point along the curve.

Outlines
00:00
📚 Introduction to Arc Length and Parametric Equations

This paragraph introduces the topic of arc length calculation in the context of parametric equations, building upon previous discussions on arc length and surface area calculations. The speaker reminds viewers of the process for finding arc length in Cartesian coordinates, which involves integrating the square root of \(1 + (f'(x))^2\) from \(A\) to \(B\). The focus then shifts to applying this concept to parametric equations, where \(x = x(t)\) and \(y = y(t)\), instead of a single function \(f(x)\). The goal is to derive an equivalent expression for arc length in terms of parametric variables, setting the stage for a deeper exploration of the topic.

Mindmap
Keywords
💡Arc Length
Arc length refers to the measure of the distance along the curve of a function. In the video, arc length is the main topic discussed in the context of parametric equations. The script explains how to find the arc length by integrating a function, which is crucial for understanding the length of a curve when it is not in the standard Cartesian form but defined parametrically.
💡Parametric Coordinates
Parametric coordinates are a way of expressing the coordinates of points on a curve using a parameter, often denoted as 't' for time. In the video, the concept of parametric coordinates is central as it discusses how to find the arc length of a curve when it is defined in terms of parametric equations rather than the standard y = f(x) form.
💡Parametric Equations
Parametric equations are equations that define the coordinates of points on a curve in terms of a third variable, usually 't'. The video script explains that these equations are used when the curve is not directly given by a function of x but instead by separate equations for x and y in terms of 't'.
💡Integration
Integration is a fundamental concept in calculus that involves finding the accumulated quantity of a variable, such as the length of a curve. In the video, integration is used to calculate the arc length by integrating the square root of the derivative squared, which is a method to find the length of a curve defined parametrically.
💡Derivative
The derivative in calculus represents the rate of change of a function with respect to its variable. In the context of the video, the derivative is essential for finding the arc length formula in parametric equations, as it involves taking the derivative of the parametric functions x(t) and y(t) with respect to 't'.
💡Surface Area
Surface area, as mentioned in the script, is related to the concept of arc length when a function is rotated around an axis. While not the main focus of the video, the script refers to how arc lengths are used in calculating the surface area of solids of revolution, which is an application of the arc length concept.
💡Square Root
The square root is a mathematical operation that finds a value which, when multiplied by itself, gives the original number. In the video, the square root is used in the arc length formula to ensure the result is a positive value, representing the actual distance along the curve.
💡Variable 't'
The variable 't' is commonly used in parametric equations to represent time or a parameter that varies. In the video, 't' is used to denote the parameter in parametric equations x(t) and y(t), which are essential for finding the arc length of a curve defined in this way.
💡Cartesian Coordinates
Cartesian coordinates are a two-dimensional coordinate system where each point is defined by an ordered pair (x, y). The video script contrasts this with parametric coordinates, explaining that the arc length formula for Cartesian coordinates involves integrating the square root of 1 plus the derivative of the function squared.
💡Function of X
A function of x, often denoted as f(x), is a mathematical expression that assigns a unique output for each input. The video script discusses how the standard arc length formula is derived for functions of x and then extends this concept to parametric equations where the function is not directly given as f(x) but through x(t) and y(t).
Highlights

Introduction to the topic of arc length and parametric coordinates in advanced calculus.

Connection between previous sections on arc length and surface area to the current topic.

Explanation of the transition from Cartesian coordinates to parametric equations.

Overview of how to write functions in terms of parametric equations with variable T.

Introduction of the arc length formula in terms of parametric equations.

Comparison of the arc length formula in Cartesian coordinates versus parametric equations.

Description of the process to find arc length when the function is given in terms of X(T) and Y(T).

Explanation of the integral formula for arc length in Cartesian coordinates.

Conversion of the arc length integral formula to apply to parametric equations.

Illustration of the concept of finding arc length with a visual example.

Detailed explanation of the steps to derive the arc length formula for parametric equations.

The importance of understanding the derivative and its role in the arc length formula.

Clarification on the notation and variables used in parametric equations (X(T), Y(T)).

Guidance on how to apply the arc length formula to parametric equations for problem-solving.

Emphasis on the similarity in concept between Cartesian and parametric arc length calculations.

Encouragement to review previous sections for a deeper understanding of the topic.

Final summary of the process to find the arc length of a function defined by parametric equations.

Transcripts

Browse More Related Video

Lesson 12 - Surface Area Of Revolution In Parametric Equations

Arc Length Calculus Problems,

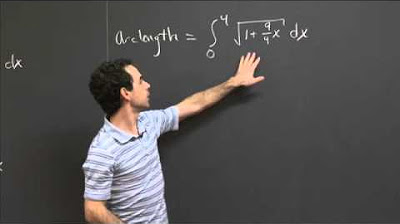
Arc Length of y=x^(3/2) | MIT 18.01SC Single Variable Calculus, Fall 2010

Finding Arc Length Using an Integral

Lec 32 | MIT 18.01 Single Variable Calculus, Fall 2007

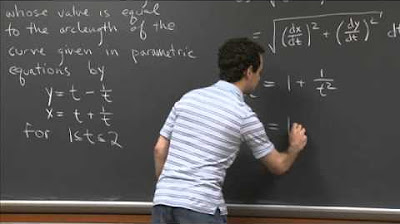
Parametric Arclength | MIT 18.01SC Single Variable Calculus, Fall 2010

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Advanced CalculusArc LengthParametric EquationsMath TutorialEducational ContentIntegral CalculusSurface AreaFunction DerivativesCalculus ConceptsParametric Coordinates