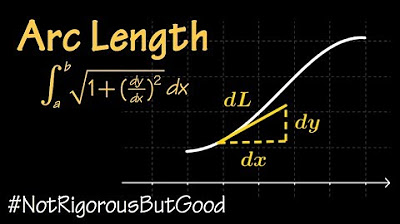2011 Calculus BC free response #1d | AP Calculus BC | Khan Academy
TLDRThe video script explains the process of calculating the total distance traveled by a particle over a given time interval, using the concept of arc length. It starts by identifying the coordinates of the particle at times t=0 and t=3, then introduces the idea of breaking down the path into small segments, using the Pythagorean theorem to approximate the length of these segments. The script derives the arc length formula by considering the derivatives of the x and y coordinates with respect to time and emphasizes the utility of this formula in the AP exam setting. Finally, it demonstrates how to use a calculator to find the definite integral that represents the total distance, resulting in a distance of 21.091 units.
Takeaways
- 📌 The problem involves finding the total distance traveled by a particle over a time interval from t=0 to t=3.
- 📍 The initial position at t=0 is identified as (0, -4), and the final position at t=3 is (21, -3.226).
- 🛤️ The path of the particle is unknown but can be approximated and plotted if desired.
- 📐 The arc length formula is derived from the Pythagorean theorem, relating small changes in x and y (dx and dy) to the differential dt.
- 🔄 The arc length formula is expressed as √(dx² + dy²), which simplifies to √[(x'(t)dt)² + (y'(t)dt)²].
- 🎓 The derivatives x'(t) and y'(t) are given as 4t + 1 and sin(t)² respectively.
- 🧮 The total arc length is found by integrating the derived formula from 0 to 3 with respect to t.
- 📊 The integral is calculated using a calculator, which is allowed in the context of the AP exam.
- 🤔 The process involves understanding the concept of differentials and how they relate to the path of a particle.
- 🏁 The final calculated distance that the particle traveled is 21.091 units.
- 📝 The problem-solving approach emphasizes the importance of understanding the underlying principles and the ability to apply them to derive and solve for the arc length.
Q & A
What is the problem being discussed in the transcript?
-The problem involves calculating the total distance traveled by a particle over a time interval from t=0 to t=3.
How is the starting point of the particle's path determined?
-The starting point is determined by the given values of x(0) and y(0), which are 0 and -4, respectively, placing the particle at the coordinates (0, -4) at time t=0.
What are the coordinates of the particle at the end of the time interval?
-At the end of the time interval (t=3), the particle is at the coordinates (21, approximately -3.226).
What is the purpose of drawing axes and plotting points in this context?
-Drawing axes and plotting points help visualize the path of the particle and understand the problem better, although it's not always necessary under time pressure during an exam.
What is the significance of the arc length formula in this problem?
-The arc length formula is used to calculate the total distance traveled by the particle along its path between the two given time points.
How is the small change in x along the path represented?
-The small change in x along the path is represented by dx, and similarly, the small change in y is represented by dy.
What is the relationship between differentials and derivatives in the context of arc length?
-In the context of arc length, differentials dx and dy are related to their respective derivatives by the expressions dx = x'(t) dt and dy = y'(t) dt.
How is the integral used to find the total arc length?
-The integral is used to sum up all the infinitely small arc lengths from t=0 to t=3, which gives the total distance traveled by the particle.
What are the expressions for x'(t) and y'(t) given in the problem?
-The expressions given are x'(t) = 4t + 1 and y'(t) = sine(t) squared.
What is the final calculated total distance traveled by the particle?
-The final calculated total distance traveled by the particle is approximately 21.091 units.
How does the use of a calculator simplify the process of finding the arc length?
-The use of a calculator simplifies the process by allowing us to find the definite integral of the complex function without having to manually find the antiderivative.
Outlines
📏 Calculating Total Distance Traveled
This paragraph introduces the task of calculating the total distance traveled by a particle over a given time interval, specifically from t=0 to t=3. The speaker begins by setting up a coordinate system to visualize the starting point (0, -4) at t=0 and the ending point at t=3, which is found to be (21, -3.226). The main focus is on understanding the concept of arc length and how to derive the formula for it. The speaker explains the process of breaking down the path into small segments, using the Pythagorean theorem to approximate the length of these segments, and then expressing these lengths as functions of time (x'(t) and y'(t)). The paragraph concludes with the integral formula for arc length, which is derived by multiplying the speed function by the differential dt and integrating over the given time interval.
🧮 Deriving Arc Length Formula and Solving with a Calculator
The second paragraph delves into the specifics of the arc length formula derived in the previous section. The speaker simplifies the formula by factoring out dt and expressing it in terms of the derivatives x'(t) and y'(t). The goal is to find the total arc length by integrating this expression from t=0 to t=3. The derivatives x'(t) = 4t + 1 and y'(t) = sin(t)^2 are provided, and the speaker emphasizes the use of a calculator to evaluate the definite integral. The paragraph concludes with the result of the calculation, which is 21.091, representing the total distance traveled by the particle over the specified time interval.
Mindmap
Keywords
💡arc length
💡particle
💡time interval
💡differentials
💡Pythagorean theorem
💡derivatives
💡integral
💡AP exam
💡x'(t) and y'(t)
💡definite integral
💡calculator
Highlights
The problem involves finding the total distance traveled by a particle over a time interval.
The particle's path is described by specific functions for x and y coordinates over time.
At time t=0, the particle is at the point (0, -4).
At time t=3, the particle reaches the point (21, -3.226).
The path of the particle can be visualized and plotted, although it might be complex.
The total distance traveled is equivalent to the length of the particle's path.
The arc length formula can be applied to find the total distance, but it may be forgotten or complex to use directly.
A re-derivation of the arc length formula is suggested for a better understanding of its application.
The small change in arc length can be approximated by the hypotenuse of a right triangle formed by small changes in x and y.
The derivatives of x and y with respect to time are used to express changes in distance as functions of time.
The arc length formula is derived from the Pythagorean theorem and the concept of differentials.
The integral of the derived arc length formula from t=0 to t=3 will give the total distance traveled.
The use of calculators is allowed and recommended to find the definite integral in the AP exam setting.
The final calculated distance is approximately 21.091 units.
The process of deriving and applying the arc length formula is valuable for understanding its purpose and function.
The problem-solving approach combines theoretical knowledge with practical application of mathematical concepts.
The example serves as a comprehensive review of the concepts of calculus, specifically related to parametric equations and arc length.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: