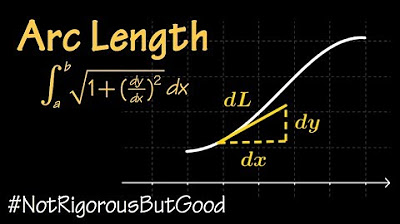Lesson 8 - Arc Length (Calculus 2 Tutor)

Math and Science
18 Aug 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThis advanced calculus tutorial introduces the concept of arc length, a new topic following integration techniques. The instructor explains that arc length is the measure of a curve's length on a graph, which can be challenging to determine with a straight ruler. The video will cover a basic proof to derive a formula for calculating arc length, which is essential for finding the length of oddly shaped curves. The method involves dividing the curve into infinitesimally small segments, summing their lengths, and taking a limit as the segments approach zero, showcasing calculus' power in determining real-world measurements.

Takeaways
  • 📚 The video introduces a new topic in calculus: arc length.
  • 🔍 Arc length is the measure of the distance along a curve between two points.
  • 📏 The concept is different from measuring straight lines with a ruler.
  • 📈 Calculus is useful for finding the length of complex shapes, such as curved graphs.
  • 📉 The video will cover a formula to calculate arc length using calculus.
  • 📝 The process involves dividing the curve into infinitesimally small segments.
  • 📐 These small segments are then summed up to find the total arc length.
  • 📚 The formula derivation will be explained, providing a foundation for solving arc length problems.
  • 📖 The video will include several practice problems to apply the arc length formula.
  • 🔑 Understanding previous calculus concepts is important, but the arc length topic is distinct.
  • 🎯 The ultimate goal is to find a numerical value for the arc length in real-world units.
Q & A

  • What topic is being discussed in this section of the advanced calculus tutorial?

    -The topic being discussed is arc length, which is a new topic different from the previous sections on integration techniques.

  • Why is calculus useful for finding the length of a curved line?

    -Calculus is useful because it can help find the length of odd shapes and complicated figures, such as the arc length of a curve, which is difficult to measure with a straight ruler.

  • What does the term 'arc length' refer to in the context of calculus?

    -Arc length refers to the length of a curve or a section of a curve on a graph, which can be calculated using calculus when it's not a straight line.

  • How does one typically measure the length of a straight line?

    -The length of a straight line is typically measured by holding a ruler up to it and observing the distance it covers.

  • What is the challenge with measuring the length of a curved line using a straight ruler?

    -The challenge is that a straight ruler does not conform to the shape of a curved line, making it difficult to accurately measure the length of the curve.

  • What is the general approach used in calculus to derive formulas for complex problems?

    -The general approach involves dividing the problem into small segments, finding an equation that represents each small part, and then taking the limit as these segments become infinitesimally small to find the total.

  • What does the script imply about the importance of knowing previous calculus techniques before starting on arc length?

    -The script implies that while the arc length is a new topic, the knowledge of previous calculus techniques is important and foundational for understanding the new material.

  • Can you provide an example of how calculus might be used to find the arc length of a curve?

    -The script does not provide a specific example, but it suggests that calculus involves adding up infinitesimally small segments of the curve to find the total arc length.

  • What are the units that one might expect when calculating arc length?

    -The units of arc length could be in inches, meters, miles, or any other unit of length, depending on the coordinate system being used.

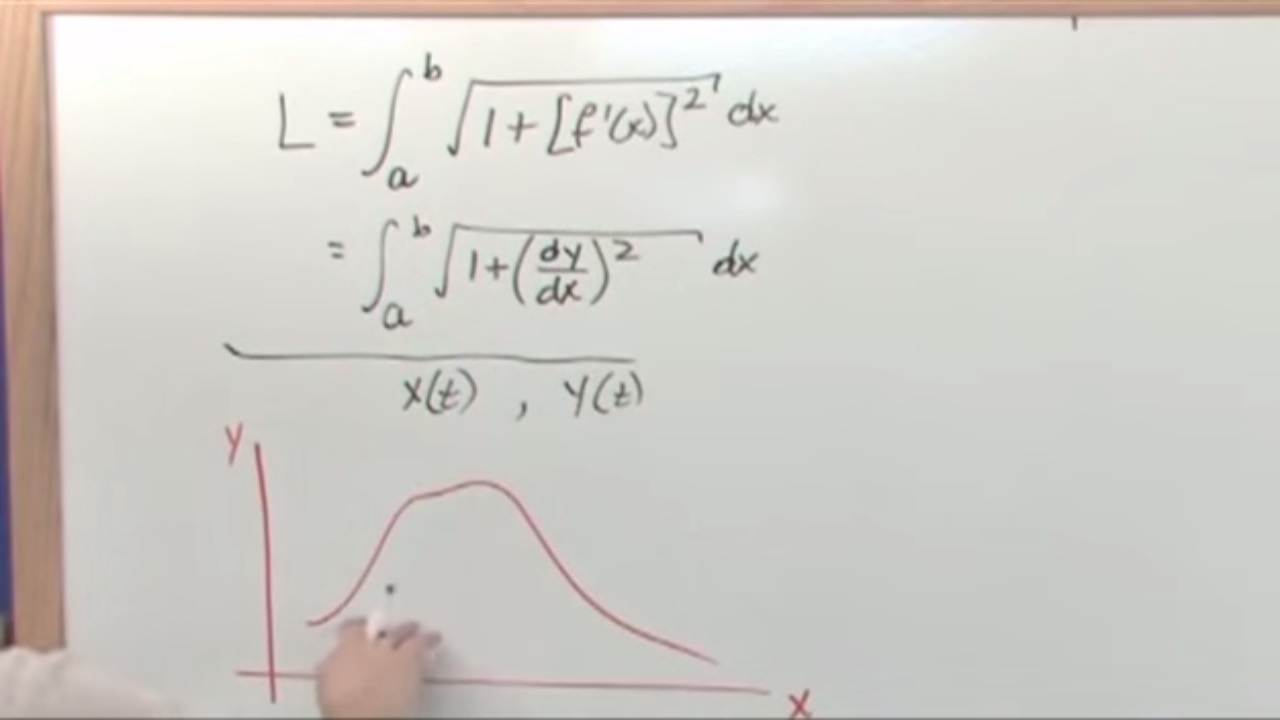
  • What is the significance of points 'a' and 'b' in the context of finding arc length?

    -Points 'a' and 'b' represent the starting and ending points on the x-axis, defining the specific section of the curve for which the arc length is to be calculated.

  • How does the script describe the process of transitioning from one topic to another in an advanced calculus course?

    -The script describes the transition as a 'grocery bar' or a break, indicating a pause from the previous integration techniques to start a new set of topics including arc length.

Outlines
00:00
📚 Introduction to Arc Length in Calculus

This paragraph introduces a new section on arc length within the context of advanced calculus. The speaker transitions from previous topics on integration techniques to a new subject matter. The concept of arc length is explained as the measurement of the distance along a curve, contrasting with the straightforward measurement of a straight line using a ruler. The paragraph sets the stage for a series of lessons that will delve into calculating the length of arcs, even complex and squiggly ones, using calculus. The speaker emphasizes the utility of calculus in determining the length, volume, and surface area of intricate shapes, which is one of the many applications of the field.

Mindmap
Keywords
💡Arc Length
Arc length is the concept of measuring the distance along a curve. In the context of the video, it refers to the length of a curve on a graph, which is a fundamental topic in calculus. The script introduces arc length as a way to calculate the distance of a curve between two points, which is not a straight line and thus cannot be measured with a ruler directly. The video aims to teach viewers how to use calculus to find the arc length of a function, which is a practical application of the subject.
💡Integration Techniques
Integration techniques are methods used in calculus to find the integral or the area under a curve. The script mentions that the video is transitioning from covering various integration techniques such as partial fractions and trigonometric integrals to a new topic. These techniques are foundational to understanding more complex concepts like arc length, as they provide the mathematical tools necessary for the calculations involved.
💡Trigonometric Integrals
Trigonometric integrals involve integrating functions that contain sine and cosine terms. The script refers to these as one of the integration techniques covered in previous sections. They are relevant to the video's theme as they represent a part of the broader set of mathematical skills that are necessary to understand and calculate arc length.
💡Inverse Trigonometric Functions
Inverse trigonometric functions are the reverse of the basic sine, cosine, and tangent functions and are used to find angles when the ratio of the sides of a triangle is known. The script mentions these functions as part of the integration techniques previously discussed. They are important in the context of the video as they can be integral to solving certain types of integrals and may relate to the curvature of a function, which is relevant to arc length.
💡Hyperbolic Functions
Hyperbolic functions are a set of functions that have a similar form to the trigonometric functions but are based on hyperbolas instead of circles. The script briefly mentions these functions in the list of topics covered before the transition to arc length. While not directly related to arc length, they represent the diverse mathematical concepts that a student of calculus would encounter.
💡Calculus
Calculus is a branch of mathematics that deals with rates of change and accumulation. The script positions the video within the broader context of a calculus tutorial, indicating that the topic of arc length is part of a larger curriculum. Calculus is central to the video's theme as it is the mathematical framework used to calculate arc lengths and other complex measurements.
💡Graph
A graph in mathematics is a visual representation of the relationship between two or more variables. The script uses the term 'graph' to describe the visual aspect of a function where the arc length is to be measured. The concept of a graph is fundamental to understanding how to calculate arc length, as it provides the visual representation of the curve whose length is being determined.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs. In the script, the term 'function' is used to describe the mathematical expression that defines the curve whose arc length is to be calculated. Functions are essential to the video's theme as they provide the formulaic representation of the curve, which is necessary for the arc length calculations.
💡X-Axis
The x-axis is the horizontal axis in a Cartesian coordinate system. The script refers to the x-axis as the reference point for the start and end of the curve on the graph. It is used to define the interval over which the arc length is to be measured, with 'a' and 'b' representing the starting and ending points on the x-axis.
💡Limit
In calculus, a limit is the value that a function or sequence approaches as the input approaches some value. The script mentions taking the limit as the segments approach zero, which is a fundamental concept in calculus used to define continuity and to derive formulas for areas, volumes, and in this case, arc lengths. The concept of the limit is crucial to understanding how to sum an infinite number of infinitesimally small segments to find the total arc length.
Highlights

Introduction to a new topic of arc length in advanced calculus.

Transition from integration techniques to a different concept.

Explanation of what arc length represents in the context of a graph.

Discussion on the difficulty of measuring the length of a curved line.

Introduction of calculus as a tool for finding lengths of complex shapes.

Illustration of how to graphically represent the arc length between two points.

Clarification that a function is required to represent the curve whose length is to be found.

Objective to find the actual length of the function between two points.

Explanation of the units that will be used to measure the arc length.

Introduction of the calculus method for deriving the formula for arc length.

Description of the process of dividing the arc into infinitesimally small segments.

Explanation of how to sum up the lengths of these small segments to find the total arc length.

Emphasis on the importance of the limit as the segments approach zero in size.

Promise of a basic proof and derivation of the arc length formula.

Anticipation of practicing the formula with several problems.

Highlighting the utility of calculus in real-life applications for measuring lengths.

Transcripts

Browse More Related Video

Arc Length (formula explained)

Arclength

AP Calculus BC Lesson 8.13

Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

Calculus 3 Lecture 12.3: Arc Length/Parameterization, TNB (Frenet-Serret) Intro

How long is a curve?? The Arclength Formula in 3D

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Advanced CalculusArc LengthIntegration TechniquesTrigonometric IntegralsPartial FractionsInverse TrigonometricHyperbolic FunctionsCalculus TutorialMathematical AnalysisEducational Content