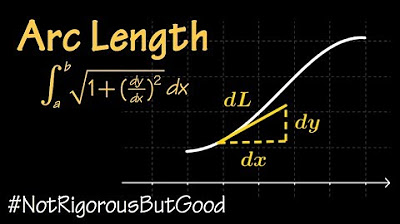How long is a curve?? The Arclength Formula in 3D

Dr. Trefor Bazett
13 Oct 201907:10
EducationalLearning
32 Likes 10 Comments

TLDRThis video explores the concept of calculating the arc length of a curve defined by a vector-valued function of a parameter T. The process begins with approximating the curve with straight line segments, then refines the approximation by increasing the number of segments. The formula for arc length is derived using the Pythagorean theorem for the segments, leading to an integral involving the derivatives of the vector components with respect to T. The video provides a clear explanation of the mathematical steps and encourages viewers to engage with the content by asking questions and exploring the multivariable calculus playlist for more.

Takeaways
  • πŸ“ The script discusses the concept of calculating the length of a curve defined by a vector-valued function \( \mathbf{r}(t) \) where the parameter \( t \) varies between two numbers \( a \) and \( b \).
  • πŸ“‰ The initial approach to finding the length of a curve involves approximating it with straight lines, dividing the curve into \( n \) equal segments.
  • πŸ“ The length of each straight line segment is calculated using the Pythagorean theorem, considering the differences in x, y, and z components of the points.
  • πŸ” By increasing the number of segments \( n \), the approximation of the curve with straight lines becomes more accurate, approaching the actual length of the curve.
  • πŸ“š The arc length of the curve is approximately equal to the sum of the lengths of these straight line segments, which is a good approximation for sufficiently large \( n \).
  • ∫ The final formula for the arc length is derived using the limit of the sum of the lengths of the line segments as \( n \) approaches infinity, which is represented by an integral.
  • πŸ“ˆ The integral formula for the arc length involves the square root of the sum of the squares of the derivatives of the x, y, and z components of the vector function with respect to the parameter \( t \).
  • πŸ“ The notation used in the script is \( f(t) \) for the x-component, \( g(t) \) for the y-component, and \( h(t) \) for the z-component of the vector function.
  • πŸ”‘ The formula for arc length is applicable as long as the vector-valued function is differentiable, allowing for the computation of the derivatives required in the formula.
  • πŸ“Š The script suggests that even though some integrals might be difficult to solve analytically, numerical integration methods can be used to find the arc length.
  • πŸ“š The video is part of a larger playlist on multivariable calculus, offering more content for those interested in further exploring this area of mathematics.
Q & A

  • What is the primary question addressed in the video script?

    -The primary question addressed in the video script is how to calculate the length of a curve given by a vector-valued function R(T) where T varies between two numbers, a and b.

  • Why is it necessary to approximate the curve with straight lines?

    -It is necessary to approximate the curve with straight lines because the length of straight lines is easily computable, and this approximation helps in estimating the length of the entire curve.

  • How does increasing the number of segments (n) affect the approximation of the curve's length?

    -Increasing the number of segments (n) makes the approximation more accurate as it allows for a finer division of the curve into smaller straight-line segments, thus getting closer to the actual curve shape.

  • What is the formula used to calculate the length of a straight line segment between two points in 3D space?

    -The formula used to calculate the length of a straight line segment between two points in 3D space is the square root of the sum of the squares of the differences in the x, y, and z components (Ξ”L = √(Ξ”xΒ² + Ξ”yΒ² + Ξ”zΒ²)).

  • What does the script suggest doing with the parameter T to improve the approximation?

    -The script suggests dividing the parameter T into an increasingly larger number of segments (smaller Ξ”T) to improve the approximation of the curve's length.

  • What mathematical concept is used to replace the sum of the straight line segments with an exact measure?

    -The concept of a limit is used to replace the sum of the straight line segments with an exact measure, by taking the limit as the number of segments (n) approaches infinity.

  • What is the final formula for calculating the arc length of a curve?

    -The final formula for calculating the arc length of a curve, assuming the vector-valued function R(T) is differentiable, is the integral of the square root of the sum of the derivatives of the x, y, and z components squared with respect to T (∫√(f'(t)² + g'(t)² + h'(t)²) dt), where f, g, and h are the x, y, and z components of R(T), respectively).

  • What is the significance of the derivatives in the final arc length formula?

    -The derivatives in the final arc length formula represent the rate of change of the curve's x, y, and z components with respect to the parameter T, which are essential for determining the curve's shape and length.

  • Can the final arc length formula be used for any differentiable vector-valued function?

    -Yes, the final arc length formula can be used for any differentiable vector-valued function, provided that the function's components with respect to T are differentiable.

  • What is the script's suggestion for handling integrals that are difficult to solve analytically?

    -The script suggests using a numerical integrator for integrals that are difficult to solve analytically, allowing for the computation of the arc length even when an exact solution is not feasible.

Outlines
00:00
πŸ“ Calculating Curve Length Using Approximation

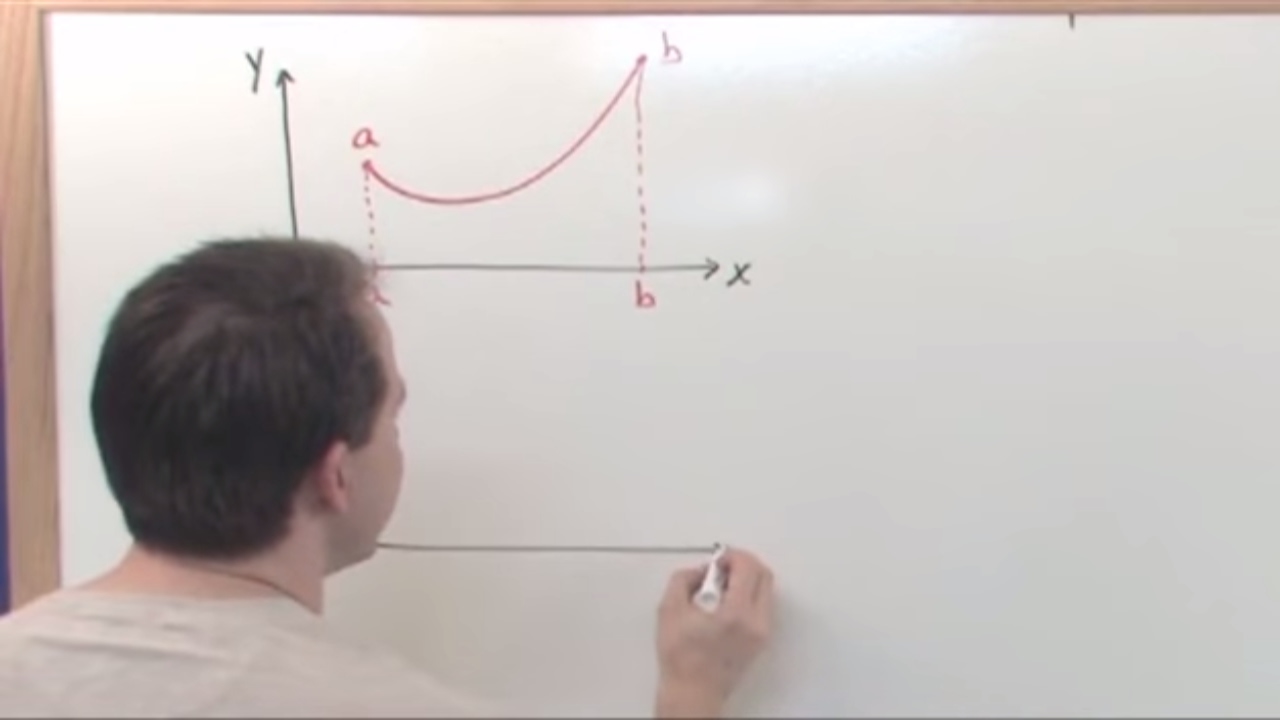
In this section, we explore how to determine the length of a curve defined by a vector-valued function \(R(t)\) with \(t\) ranging between \(a\) and \(b\). The process begins with approximating the curve using straight line segments. By dividing the interval \([a, b]\) into \(n\) equal segments, we plot the corresponding points on the graph and draw line segments between them. The total arc length of the original curve can be approximated by summing the lengths of these line segments. As \(n\) increases, the approximation becomes more accurate. The length of each segment is determined using the Pythagorean theorem. By calculating the length of a generic line segment, we obtain an expression for the arc length as the sum of these lengths, represented as a summation over the segments.

05:01
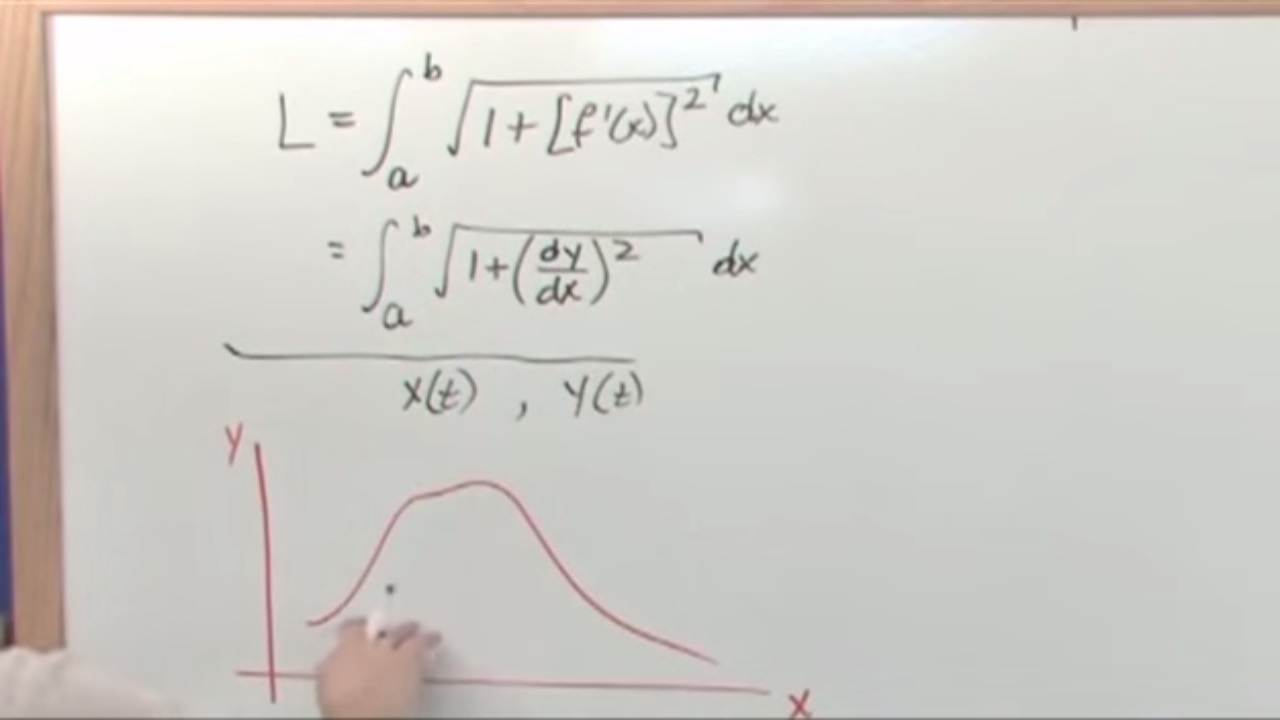
πŸ”’ From Approximation to Exact Calculation Using Limits

To move from approximation to an exact calculation, we introduce the concept of taking the limit as the number of segments \(n\) approaches infinity. This transforms the summation into an integral. By defining \(R(t)\) with components \(F(t)\), \(G(t)\), and \(H(t)\), the length of the curve can be expressed as an integral involving the derivatives of these components with respect to \(t\). This integral formula allows us to compute the exact arc length of the curve, provided the vector-valued function is differentiable. Although solving the integral might be challenging, it provides a precise mathematical expression for the arc length.

Mindmap
Keywords
πŸ’‘Vector-valued function
A vector-valued function is a function that takes one or more variables (in this case, the parameter \( t \)) and returns a vector. In the video, the curve is given by a vector-valued function \( R(t) \), where \( t \) varies between two numbers \( a \) and \( b \). This function defines the position of points along the curve.
πŸ’‘Arc length
Arc length is the measure of the distance along a curve. In the video, the main question addressed is how to determine the length of the curve defined by the vector-valued function \( R(t) \). The process involves approximating the curve with straight lines and then summing the lengths of these segments.
πŸ’‘Approximation with straight lines
This concept involves breaking the curve into smaller, straight-line segments to estimate its length. By increasing the number of segments, the approximation becomes more accurate. The video explains that the sum of these segment lengths gives an approximation of the arc length, which improves as more segments are used.
πŸ’‘Pythagorean formula
The Pythagorean formula is used to calculate the length of a straight line segment in terms of its components. In the video, it is applied to the differences in the \( x \), \( y \), and \( z \) components of points along the curve, resulting in the formula \( \Delta L_i = \sqrt{(\Delta x_i)^2 + (\Delta y_i)^2 + (\Delta z_i)^2} \).
πŸ’‘Limit
A limit is a fundamental concept in calculus used to define the value that a function approaches as the input approaches some value. In the video, taking the limit as the number of segments \( n \) goes to infinity transforms the sum of segment lengths into an integral, representing the exact arc length of the curve.
πŸ’‘Integral
An integral is a mathematical concept that represents the area under a curve or, in this case, the accumulation of lengths along a curve. The video shows how the approximation sum becomes an integral in the limit, leading to the formula for arc length as an integral of the square root of the sum of the squares of derivatives.
πŸ’‘Derivative
A derivative represents the rate of change of a function with respect to a variable. In the video, derivatives of the \( x \), \( y \), and \( z \) components of the vector-valued function \( R(t) \) with respect to \( t \) are used to compute the exact arc length. These derivatives replace the finite differences in the segment length formula as the limit is taken.
πŸ’‘Differentiable
A function is differentiable if it has a derivative at every point within its domain. The video assumes that the vector-valued function \( R(t) \) is differentiable, which allows for the use of derivatives in calculating the arc length. Differentiability ensures that the curve is smooth enough for this method to be applicable.
πŸ’‘Summation
Summation is the process of adding a sequence of numbers. In the video, summation is used to approximate the arc length by adding the lengths of straight-line segments. This summation turns into an integral as the number of segments increases indefinitely.
πŸ’‘Parameter
A parameter is a variable that is used to define a function or system. In the video, \( t \) is the parameter that varies between \( a \) and \( b \) and defines the position of points along the curve via the vector-valued function \( R(t) \). The parameter's role is crucial in setting up the interval and segments for arc length calculation.
Highlights

Introduction to the concept of calculating the length of a curve given by a vector-valued function R(T).

Parameter T is allowed to vary between two different numbers a and B.

The challenge of determining the length of a curve without it being a straight line or a circle.

Using calculus to compute the length of 'nice' differentiable curves.

Approximating the curve with straight lines by dividing the interval into n equal segments.

Plotting points on the graph and drawing line segments between them to approximate the curve.

The approximation of the arc length as the sum of the lengths of these straight line segments.

Increasing the number of segments (n) to improve the approximation of the curve's length.

Zooming in on a specific straight-line segment to understand its length calculation.

Using the Pythagorean formula to calculate the length of a straight line segment in 3D space.

The process of summing the lengths of all small line segments to approximate the arc length.

Multiplying the sum by a version of one to prepare for the transition to derivatives.

Replacing finite differences with derivatives as the number of segments approaches infinity.

Defining the arc length as the limit of the sum of the lengths of the line segments as n approaches infinity.

Introducing the integral formula for arc length involving the derivatives of the vector components.

Setting the notation for the x, y, and z components of the vector function R(T).

Final formula for arc length using the integral of the square root of the sum of derivatives squared.

The possibility of using numerical methods to evaluate the integral for arc length.

Invitation for viewers to leave questions in the comments for further discussion.

Encouragement for viewers to like the video to support the content creators.

Promotion of a playlist of multivariable calculus videos for further learning.

Transcripts

Browse More Related Video

Arc Length (formula explained)

2011 Calculus BC free response #1d | AP Calculus BC | Khan Academy

AP Calculus BC Lesson 8.13

Curvature of a cycloid

Lesson 8 - Arc Length (Calculus 2 Tutor)

Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Arc LengthCalculusVector FunctionsDifferentiationIntegrationCurve ApproximationMultivariableMathematicsEducationalNumerical Methods