Ch. 13.1 Finding Limits Numerically and Graphically

Prof. Williams
6 May 202208:06
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script delves into the concept of limits in calculus, focusing on left and right hand limits and their significance in determining the behavior of functions as they approach a certain value. The instructor revisits the topic, having previously covered it in the context of rational functions and vertical asymptotes. The script also illustrates the numerical method for analyzing limits by plugging in values close to the point of interest, highlighting the importance of consistency between the left and right hand limits for the existence of a limit. Examples, including the sine function and a piecewise function, are used to demonstrate the application of these concepts.

Takeaways
  • 📚 The class is covering the last chapter, Chapter 13, with a focus on limits in calculus.
  • 🔍 Limits were previously discussed in Chapter 3, specifically in sections 3.5 and 3.6, in the context of rational functions and vertical asymptotes.
  • 📉 The concept of limits at infinity, or long-term behavior of functions, is also part of the discussion.
  • 📌 The limit of a function as x approaches a certain number is a value, unless it does not exist or approaches positive or negative infinity.
  • 👉 The approach to a specific value c involves examining the behavior of the function from both the left (c-) and right (c+) sides.
  • 📈 Numerical methods for analyzing limits involve plugging in values of x that get progressively closer to the value c.
  • 🤔 If the left and right hand limits approach the same value, the limit of the function exists; if not, the limit does not exist at that value of c.
  • 📊 The function sin(|x|)/x is used as an example to illustrate how limits are evaluated as x approaches zero, revealing that the limit does not exist due to differing left and right hand limits.
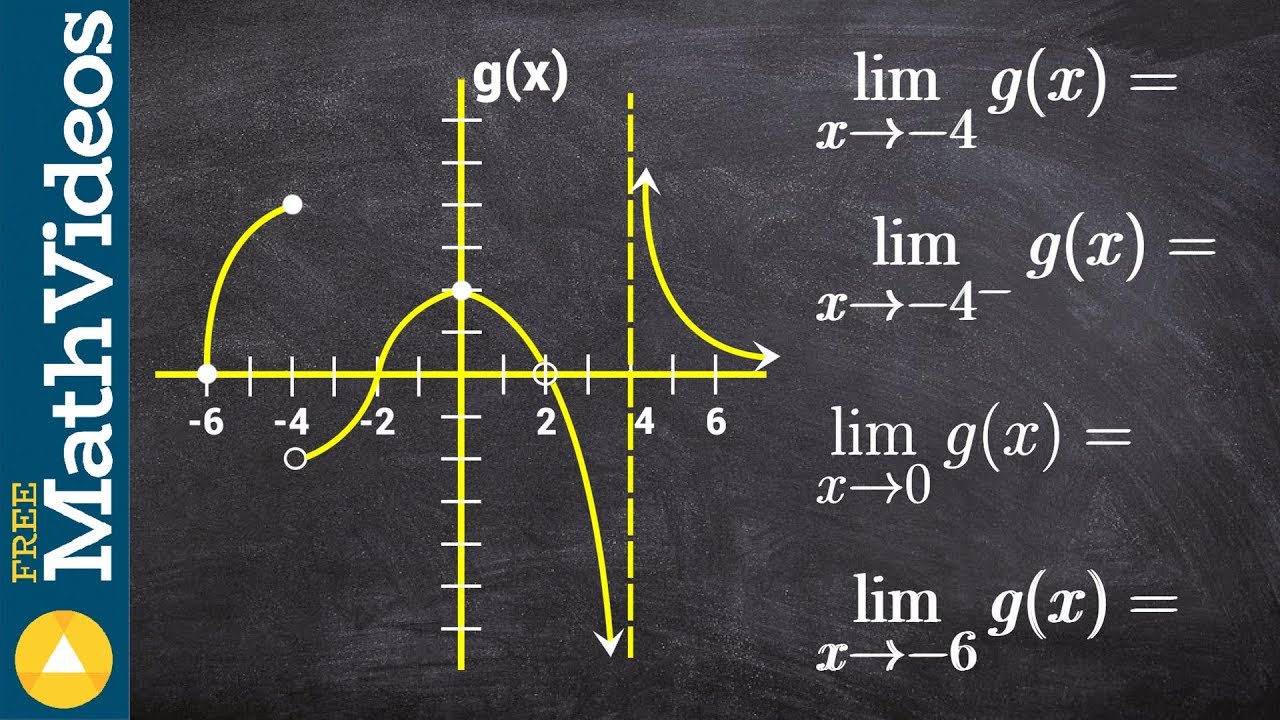
  • 📐 A piecewise function graph is analyzed to demonstrate how to determine if a limit exists by comparing the left and right hand limits as x approaches specific values.
  • 🚫 At x = -4, the limit does not exist because the left and right hand limits do not agree, indicating different values are approached from each side.
  • 🆗 At x = 2, the left and right hand limits both approach the same value, confirming the existence of the limit at that point.
Q & A

  • What is the main focus of the last chapter of the video series?

    -The main focus of the last chapter is on the introduction to calculus, specifically on limits, including left and right hand limits.

  • In which previous chapters were limits discussed in the video series?

    -Limits were discussed in the rational functions portion of chapter three, specifically around sections 3.5 and 3.6.

  • What is the definition of a limit in the context of a function?

    -The limit of a function as x approaches a certain number is the value that the function approaches if it is not a value, then the limit either doesn't exist or is positive or negative infinity.

  • What are the two sides from which we approach a value when discussing limits?

    -When discussing limits, we approach a value from the left side, denoted as c negative, and from the right side, denoted as c raised to a plus.

  • What is the numerical method for analyzing limits?

    -The numerical method for analyzing limits involves plugging in values of x that are increasingly closer to the value c from both the left and right sides.

  • What does it mean if the left and right hand limits agree with each other?

    -If the left and right hand limits agree, meaning they approach the same value, then the limit of the function exists and is equal to that value.

  • What happens if the left and right hand limits do not agree?

    -If the left and right hand limits do not approach the same value, then the function does not have a limit at that value of c.

  • What is the function being analyzed in the example with sine and absolute value of x divided by x?

    -The function being analyzed is sine of the absolute value of x divided by x, and the focus is on what happens near zero.

  • What is the observed behavior of the function as x approaches zero from both the positive and negative sides in the given example?

    -As x approaches zero from the positive side, the function approaches a value of one. From the negative side, it approaches negative one. Since these do not match, the limit at zero does not exist.

  • What is a piecewise function and how does it relate to the script?

    -A piecewise function is a function that is defined by different expressions over different intervals of its domain. The script discusses analyzing the behavior of a piecewise function as it approaches certain values.

  • What is the conclusion about the limit as x approaches 2 in the piecewise function example?

    -The conclusion is that the limit as x approaches 2 exists and is 4, because both the left and right hand limits agree and approach the same value.

Outlines
00:00
📚 Introduction to Limits in Calculus

The instructor begins by introducing the last chapter of the current section, focusing on the concept of limits in calculus. They remind students that limits were previously discussed in the context of rational functions and vertical asymptotes. The summary explains the fundamental idea of a limit, emphasizing the difference between left and right hand limits and their significance in understanding the behavior of functions as they approach a specific value. The instructor also introduces numerical methods for analyzing limits by plugging in values close to the point of interest and comparing the behavior from both sides of the number line.

05:03
🔍 Analyzing Limits with Numerical Methods and Graphs

This paragraph delves deeper into the numerical method of analyzing limits by providing a step-by-step example using the sine function of the absolute value of x divided by x. The instructor illustrates how to approach the limit as x gets closer to zero from both the positive and negative sides, highlighting the discrepancy in the values approached from each side, which indicates that the limit does not exist at x=0 for this function. The explanation is followed by another example involving a piecewise function, where the instructor examines the behavior of the function as it approaches specific points, such as negative four and positive two, to demonstrate how left and right hand limits can either agree, indicating the existence of a limit, or disagree, signifying the non-existence of a limit at that point.

Mindmap
Keywords
💡Chapter 13
In the context of the video, 'Chapter 13' refers to the final chapter that the instructor plans to cover in the current section of the course. It is part of a larger educational series and signifies the progression through the material, with the instructor indicating that this chapter, along with the next two, will be sufficient for students to understand the basics of calculus.
💡Calculus
Calculus is a branch of mathematics that deals with rates of change and accumulation. In the video, calculus is the overarching subject matter, with the instructor preparing students for a deeper dive into the topic in an upcoming series. The concept of limits is foundational to calculus and is the main focus of the script.
💡Limits
Limits are a fundamental concept in calculus that describe the value that a function or sequence 'approaches' as the input or index approaches some value. In the script, the instructor discusses how limits have been previously introduced in the context of rational functions and vertical asymptotes, highlighting their importance in understanding the behavior of functions.
💡Left and Right Hand Limits
These terms refer to the behavior of a function as the input approaches a certain value from the left (negative side) or the right (positive side). The instructor emphasizes the importance of evaluating both to determine the existence of a limit at a particular point, using the function 'sine of absolute value of x divided by x' as an example to illustrate the concept.
💡Vertical Asymptotes
A vertical asymptote is a vertical line that a graph approaches but never intersects. It occurs where a function is undefined or unbounded. In the script, the instructor mentions discussing vertical asymptotes in previous chapters, where left and right hand limits were used to analyze the behavior of functions near these asymptotes.
💡Long-term Limits
Long-term limits, also known as limits at infinity, describe the behavior of a function as the input approaches infinity or negative infinity. The instructor briefly mentions this concept to highlight the different types of limits that are discussed in the calculus course.
💡Numerical Methods
Numerical methods in the context of limits involve plugging in values of x that are increasingly close to the point of interest (c) to observe the function's behavior. The instructor uses this approach to demonstrate how to approximate limits by providing values from both sides of the point in question.
💡Function Behavior
Function behavior refers to how a function's output changes in response to its input. The script discusses analyzing this behavior as the input approaches a specific value, which is central to understanding limits and their significance in calculus.
💡Piecewise Functions
A piecewise function is a function that is defined by multiple pieces, each with its own expression. The instructor uses a piecewise function in the script to illustrate how limits can be evaluated differently depending on the piece of the function being considered.
💡Asymptotic Behavior
Asymptotic behavior refers to the long-term behavior of a function as it approaches a certain value or infinity. In the script, the instructor discusses how limits can indicate whether a function approaches an asymptote or tends towards positive or negative infinity.
💡Graph Analysis
Graph analysis is the process of visually examining a graph to understand the behavior of a function. The instructor uses graph analysis to demonstrate how to determine the existence of limits by observing the function's values as it approaches certain points, such as in the example of the sine function.
Highlights

Introduction to the last chapter of the section, focusing on calculus.

Limit discussions from previous chapters will be built upon.

Explanation of limits, including left and right hand limits and long term behavior.

The concept that the limit of a function as x approaches a number is a value or infinity.

Approaching a specific value c from the left (c-) and right (c+).

If function values approach the same limit from both sides, the limit exists.

Demonstration of numerical methods to analyze limits by plugging in values close to c.

Example using the sine function to illustrate limits as x approaches zero.

Observation that the sine function approaches different values from negative and positive sides of zero.

Conclusion that the limit does not exist for the sine function at x=0 due to non-matching sides.

Introduction of a piecewise function and its behavior as x approaches specific values.

Analysis of the piecewise function's limit as x approaches -4 from both sides.

Identification of non-existence of limit at x=-4 due to differing left and right hand limits.

Analysis of the piecewise function's limit as x approaches 2 from both sides.

Confirmation of the limit's existence at x=2 as left and right hand limits match.

Emphasis on the importance of matching left and right hand limits for the existence of a limit.

Transcripts

Browse More Related Video

Limits! Part 1

Calculus - One Sided Limits

AP Calculus AB - 1.14 Connecting Infinite Limits and Vertical Asymptotes

Evaluate all the limits from a given graph

Limits via Graphs!

A Tale of Three Functions | Intro to Limits Part II

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusLimitsAsymptotesNumerical MethodsGraphical AnalysisSine FunctionPiecewise FunctionsLeft Hand LimitRight Hand LimitVertical AsymptoteEducational Content