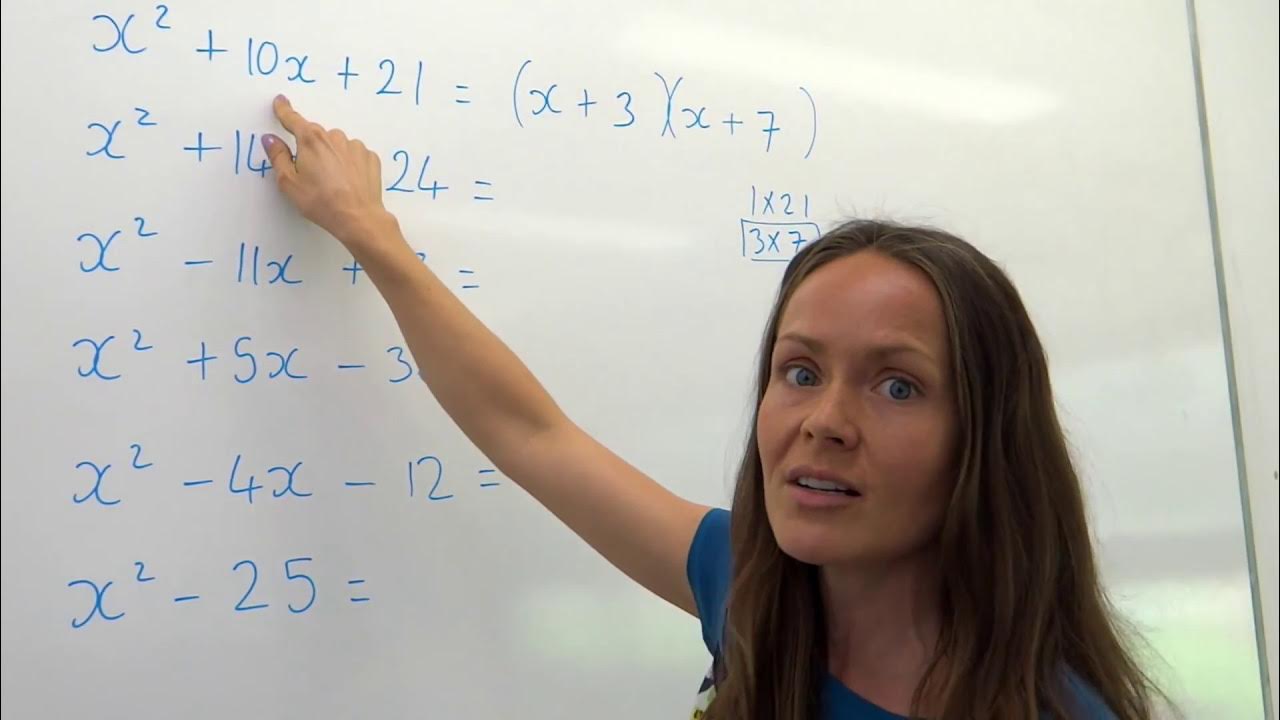Ch. 10.7 Partial Fractions
TLDRThis script covers the concept of partial fraction decomposition, a vital technique in higher-level math courses such as calculus and differential equations. The instructor explains how to break down complex rational expressions into simpler components, focusing on factoring the denominator and handling four distinct cases: distinct linear factors, linear factors with multiplicity, prime quadratic factors, and quadratic factors with multiplicity. The process involves setting up and solving systems of equations after clearing denominators. The script includes examples to illustrate the method, emphasizing the importance of this tool in advanced mathematics, physics, and engineering.
Takeaways
- 📚 The lecture introduces partial fraction decomposition, a method to break down rational expressions into simpler components.
- 🔍 Partial fractions are commonly used in higher-level mathematics and engineering courses, particularly in differential equations and calculus.
- 👨🏫 The instructor emphasizes the importance of partial fractions, as they are a frequently used tool in problem-solving.
- 📐 The process involves factoring the denominator (q) of a rational function and ignoring the numerator (p) for the decomposition.
- 🧩 There are four cases for partial fraction decomposition, based on the nature of the factors of the denominator: distinct linear factors, linear factors with multiplicity, distinct quadratic factors, and quadratic factors with multiplicity.
- 📝 The first case is the simplest, where all linear factors of the denominator are distinct and there is no multiplicity.
- 🔢 For factors with multiplicity, the decomposition includes terms that are powers of the factor up to the multiplicity, with coefficients for each power.
- 🔍 Case three involves prime quadratic factors, which are written with a linear term in the numerator, while case four includes quadratic factors with multiplicity, expanding the decomposition further.
- 📉 The process requires setting up a system of equations by equating coefficients of like terms after clearing the denominators and solving for the unknown coefficients.
- 📚 The lecture provides a step-by-step example of partial fraction decomposition, starting with factoring the denominator and ending with solving the system of equations.
- 🔄 The instructor also demonstrates a more complex example with a mixture of different factor types, showing how to handle each case in the decomposition.
Q & A
What is the main topic of Chapter 10.7 in the transcript?
-The main topic of Chapter 10.7 is partial fractions, a method used to break down rational expressions into simpler components.
Why are partial fractions important in higher-level math courses?
-Partial fractions are important in higher-level courses such as calculus and differential equations because they are a frequently used tool for simplifying complex rational expressions.
What is the purpose of partial fraction decomposition?
-The purpose of partial fraction decomposition is to take a complex rational function and break it down into a sum of simpler, smaller rational expressions.
What are the four cases for partial fraction decomposition discussed in the script?
-The four cases are: 1) All factors of the denominator are distinct and linear; 2) There is multiplicity in the linear factors; 3) There are prime quadratic factors; and 4) There are quadratic factors with multiplicity.
How does the process of partial fraction decomposition begin?
-The process begins by factoring the denominator (q) of the rational function, as the factors of q drive the decomposition.
Why is it unnecessary to factor the numerator (p) in partial fraction decomposition?
-Factoring the numerator is unnecessary because the focus is on breaking down the denominator into its factors, not simplifying the entire rational expression by canceling common factors in the numerator and denominator.
What is the first step in the process of partial fraction decomposition after factoring the denominator?
-The first step is to rewrite the rational function based on the factors present in the denominator, setting up the decomposition with unknown constants for each term.
What mathematical operation is used to eliminate the fractions in the partial fraction decomposition process?
-Clearing denominators by multiplying each term in the equation by the least common multiple (LCM) of the denominators is used to eliminate the fractions.
How does one form a system of equations in the partial fraction decomposition process?
-By equating the coefficients of corresponding powers of x on both sides of the equation after clearing the denominators, one can form a system of linear equations to solve for the unknown constants.
Can you provide an example of a partial fraction decomposition from the transcript?
-Yes, the transcript provides an example of decomposing 2x + 1 over x^2 + 3x + 2, which factors into (x + 2)(x + 1), and then decomposing it into partial fractions with constants a and b over each factor.
What is the final step in the partial fraction decomposition process after solving for the unknown constants?
-The final step is to substitute the solved constants back into the partial fraction decomposition and simplify the expression if necessary.
Outlines
📚 Introduction to Partial Fractions
This paragraph introduces Chapter 10.7 on partial fractions, emphasizing its importance in higher-level math courses like calculus and physics. The speaker explains that partial fractions involve breaking down complex rational expressions into simpler components, which is useful for problem-solving in advanced mathematics. The process is described as the opposite of combining rational expressions and is crucial for understanding the underlying structure of these mathematical objects.
🔍 Exploring Partial Fraction Decomposition Cases
The speaker delves into the specifics of partial fraction decomposition, outlining four distinct cases based on the factors of the denominator. The first case involves distinct linear factors without multiplicity. The second case addresses linear factors with multiplicity. The third case includes prime quadratic factors without multiplicity, and the fourth case deals with quadratic factors that have multiplicity. Each case is explained with respect to how the decomposition formula is adjusted to accommodate the different types of factors.
📝 Process of Partial Fraction Decomposition
The paragraph explains the step-by-step process of partial fraction decomposition. It begins with factoring the denominator (q) to understand its components, which is essential for the decomposition. The speaker then describes how to rewrite the rational function based on these factors and clear the denominators by multiplying through by the least common multiple. This leads to forming a system of equations, which can be solved using various linear algebra techniques to find the unknown coefficients in the decomposition.
📘 Example of Partial Fraction Decomposition
The speaker provides a simple example to illustrate the partial fraction decomposition process. The given rational expression has a quadratic denominator that factors into two distinct linear factors. The decomposition is straightforward, involving setting up a system of equations based on the coefficients of the expanded form and solving for these coefficients. The solution is then substituted back into the original decomposition to express the rational function as a sum of simpler fractions.
🧩 Complex Example with Mixed Factors
This paragraph presents a more complex example involving a mixture of distinct linear factors, factors with multiplicity, and a prime quadratic factor. The speaker guides through the process of factoring the denominator, setting up the partial fraction decomposition with the appropriate forms for each type of factor, and then expanding and simplifying the expression to form a large system of equations. The goal is to demonstrate how to handle more complicated scenarios in partial fraction decomposition.
🔄 Solving the System of Equations
The speaker discusses the process of solving the large system of equations resulting from the complex example. They mention various methods such as using matrix inverses, Cramer's rule, or Gaussian elimination, acknowledging the potential complexity and time-consuming nature of these methods for large systems. The paragraph concludes with the speaker using technology to find the solution to the system, which is then used to express the decomposed form of the original rational expression.
🌟 Conclusion and Transition to Chapter 11
In the final paragraph, the speaker wraps up the discussion on partial fractions and prepares the audience for the next chapter on integration techniques. They acknowledge the difficulty of integration sections but express their personal interest in the topic, inviting students to join them for the upcoming video series on integration.
Mindmap
Keywords
💡Partial Fractions
💡Rational Function
💡Factoring
💡Multiplicity
💡Linear Factors
💡Quadratic Factors
💡Decomposition
💡Clearing Denominators
💡System of Equations
💡Rational Zeros Theorem
Highlights
Introduction to partial fractions as an important tool in higher-level math courses such as differential equations and calculus.
Explanation of partial fraction decomposition as a method to break down a rational expression into simpler parts.
Importance of factoring the denominator (q) for partial fraction decomposition, with the numerator (p) being non-factorable.
Distinction between four cases for partial fraction decomposition based on the factors of the denominator: distinct linear factors, linear factors with multiplicity, prime quadratic factors, and quadratic factors with multiplicity.
Process of rewriting a rational function based on the factors of the denominator for partial fraction decomposition.
Clearing denominators by multiplying through by the least common multiple to simplify the equation.
Formation of a system of equations by equating coefficients from the expanded form of the partial fraction decomposition.
Solving the system of equations using various methods such as inverses, reduced row echelon form, or Cramer's rule.
Example of finding the partial fraction decomposition of a simple rational function with distinct linear factors.
Use of technology or shortcuts for solving complex systems of equations in partial fraction decomposition.
Example of a complex rational function with a mixture of different factor types, demonstrating the process of partial fraction decomposition.
Technique of expanding and distributing terms in the equation to prepare for forming a system of equations.
Setting up equalities based on the coefficients of like terms from the expanded equation.
Transformation of the system of equations into a matrix form for solving using methods like Gauss-Jordan elimination.
Solution of the system using technology to find the values of unknowns in the partial fraction decomposition.
Final step of simplifying the partial fraction decomposition and ensuring no fractions remain within fractions.
Anticipation of the next chapter on integration techniques, indicating the relevance of partial fractions in integration.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: