Stokes' theorem proof part 4 | Multivariable Calculus | Khan Academy
TLDRThis video script delves into the proof of Stokes' theorem, focusing on the line integral over the boundary C of a surface. It introduces a detour to discuss the parameterization of a path C1 in the xy plane and reviews the concept of line integrals for a vector field G. The script explains how to transform the line integral into the parameter domain and sets up for the parameterization of a 3D path C, which will be used to calculate the line integral of a vector field f dot dr along the path in subsequent content.
Takeaways
- 📚 The session continues the proof of Stokes' theorem, focusing on the line integral over the boundary C of a surface.
- 🔍 A detour is taken to build up to the main topic, suggesting a step-by-step approach to understanding the theorem.
- 📐 The boundary C in the xy-plane is referred to as path C1, and its parameterization is discussed with respect to the parameter t.
- 🌐 A review of vector fields and line integrals is provided, with the vector field G defined on the xy-plane and its components m and n.
- 📈 The line integral over path C1 is explained, involving the dot product of the vector field G and the differential displacement dr.
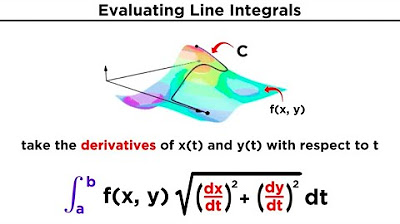
- 📝 The differential displacement dr is expressed in terms of dx and dy, which are related to the derivatives of x and y with respect to the parameter t.
- 🧩 The process of converting the line integral into the parameter domain is described, highlighting the cancellation of dt and the integration with respect to t.
- 📈 The parameterization for path C above the xy-plane is discussed, including the same x and y components but with an additional z component as a function of x and y.
- 🔑 The position vector r is introduced as a function of t to parameterize path C, with x and y being functions of t and z being a function of both x and y.
- 🔄 The script ends with the intention to continue the discussion of the line integral of f dot dr along path C in the next video.
Q & A
What is the main focus of the video script?
-The main focus of the video script is to prove the other side of Stokes' theorem, specifically calculating the line integral over the boundary C of a surface in the context of vector calculus.
What is the significance of the detour taken in the script?
-The detour is taken to build up the understanding of the concept before diving into the proof of Stokes' theorem, by focusing on a simpler region in the xy plane and its boundary path C1.
What is the role of the parameterization in the script?
-Parameterization is used to describe the path C1 in the xy plane and later the path C above the xy plane, allowing for the calculation of line integrals in terms of the parameter t.
What is the vector field G in the script?
-The vector field G is a review concept introduced in the script, defined on the xy plane as G = m(x, y)i + N(x, y)j, where m and N are functions of x and y.
How is the line integral over path C1 calculated in the script?
-The line integral over path C1 is calculated by taking the dot product of the vector field G and the differential displacement vector dr, resulting in m dx + n dy, which can be expressed in terms of the parameter t as integrals involving dx/dt and dy/dt.
What is the significance of the differential displacement vector dr?
-The differential displacement vector dr represents the infinitesimal change in position along the path and is used in the calculation of line integrals.
How does the script transition from discussing path C1 to path C?
-The script transitions by noting that while the parameterizations for x and y remain the same for both paths, path C has an additional z-component that is a function of x and y.
What is the parameterization of path C in the script?
-The parameterization of path C is given as a position vector r(t) = x(t)i + y(t)j + z(x(t), y(t))k, where x and y are functions of t, and z is a function of both x and y.
What is the purpose of the parameter t in the script?
-The parameter t is used to describe the position along the path, varying between a and b, and is crucial for evaluating the line integrals.
How does the script relate the line integral of f dot dr along path C to the parameterization?
-The script shows that the line integral of f dot dr along path C can be expressed in terms of the parameter t by substituting the parameterization of r into the integral.
Outlines
📚 Introduction to Stokes' Theorem and Line Integrals
The script begins with an introduction to the continuation of the proof of Stokes' theorem, focusing on the line integral over the boundary C of a surface, represented by the vector field f dot dr. The instructor takes a detour to clarify the concept by considering a simpler region in the xy plane, called path C1, which is the boundary of the surface. A parameterization of C1 is discussed, where x and y are functions of the parameter t, ranging from A to B. The script then reviews the concept of a vector field G defined on the xy plane, with components m and n, and explains how to calculate the line integral over path C1 by taking the dot product of G and dr, resulting in an integral involving m dx + n dy. The importance of understanding dx and dy as derivatives with respect to t is emphasized, allowing the integral to be expressed in the parameter t's domain.
🔍 Parameterization of the 3D Path C and Line Integral Setup
In the second paragraph, the focus shifts to the parameterization of the 3D path C, which lies above the xy plane. The parameterization for x and y remains the same as for C1, but now includes a z component that is a function of x and y, both of which are also functions of the parameter t. This results in a vector r(t) representing the position vector of path C, with components in the i, j, and k directions. The parameter t still varies between a and b. The script concludes with the setup for calculating the line integral of f dot dr along the path C, preparing for the continuation in the next video.
Mindmap
Keywords
💡Stokes' theorem
💡Line integral
💡Boundary
💡Parameterization
💡Vector field
💡Dot product
💡Differential
💡Integral
💡Surface
💡Function
Highlights
Continuation of the proof of Stokes' theorem with a focus on the other side of the theorem.
Exploration of the line integral over the boundary C of a surface in the context of Stokes' theorem.
Introduction of a detour to build up to the main proof.
Parameterization of the path C1 in the xy plane as the boundary of a region.
Explanation of the parameterization of C1 with x and y as functions of the parameter t.
Review of the vector field G and its components in the xy plane.
Calculation of the line integral over path C1 using the vector field G.
Dot product of the vector field G and the differential displacement dr.
Conversion of differential displacement dr into its components dx and dy.
Expression of dx and dy as derivatives with respect to the parameter t.
Transformation of the line integral into the parameter domain t.
Parameterization of the path C above the xy plane with a z component.
Introduction of the position vector r for the parameterization of path C.
Inclusion of the z component in the parameterization of C, dependent on x and y.
Anticipation of the next video to continue the discussion on the line integral of f dot dr along path C.
Transcripts
Browse More Related Video
Evaluating Line Integrals

Stokes' theorem proof part 5 | Multivariable Calculus | Khan Academy
Green's Theorem

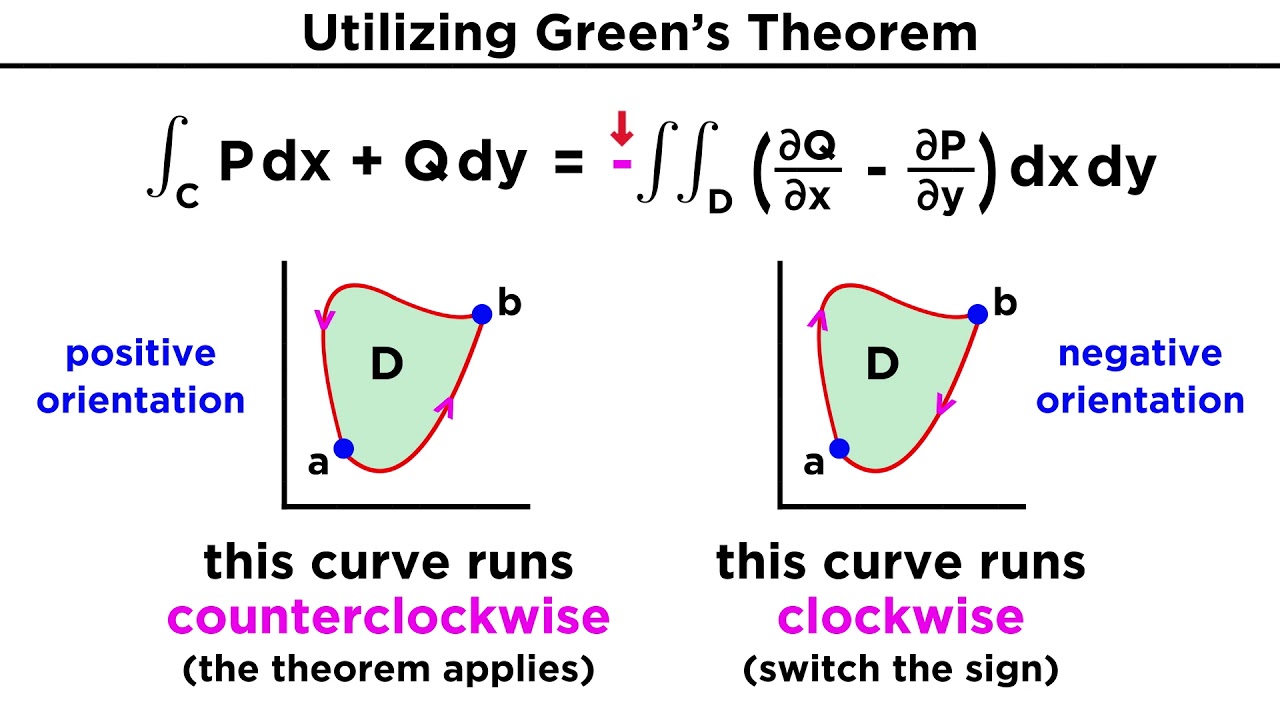
Green's theorem proof part 1 | Multivariable Calculus | Khan Academy

Green's and Stokes' theorem relationship | Multivariable Calculus | Khan Academy

Parametrization of a reverse path | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: