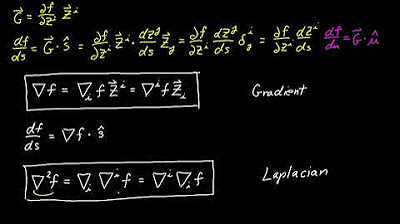Why the gradient is the direction of steepest ascent
TLDRThis video script delves into the concept of the gradient of a multi-variable function, particularly with two inputs, using the example of x squared plus y squared. It explains the gradient as a vector composed of partial derivatives, which points in the direction of steepest ascent. The script clarifies the connection between the gradient and the directional derivative, illustrating how the gradient's direction maximizes the rate of change in the function. The magnitude of the gradient indicates the rate of change in the steepest ascent direction, highlighting the gradient's significance in scalar-valued multi-variable functions.
Takeaways
- 📚 The gradient of a multi-variable function is a vector composed of partial derivatives with respect to each variable.
- 🏔️ The gradient vector points in the direction of the steepest ascent of the function, indicating the direction to increase the function value most rapidly.
- 🧭 The concept of the gradient field visualizes the direction of steepest ascent at various points in the function's domain.
- 📈 The gradient's graphical intuition relates to the x,y plane as the input space and the function's output as a mapping to a number line.
- 🤔 The connection between the gradient and the direction of steepest ascent is not immediately obvious, but the concept of the directional derivative provides insight.
- 📝 Directional derivatives measure the rate of change of a function in a specific direction, given by the dot product of the gradient and a unit vector in that direction.
- 🔍 The maximum directional derivative occurs when the unit vector aligns with the gradient, as this maximizes the dot product.
- 🔄 The magnitude of the gradient vector represents the rate of change of the function in the direction of the gradient itself.
- 🌟 The gradient is a fundamental tool in scalar multi-variable functions, extending the concept of a derivative to higher dimensions.
- 🔢 The length of the gradient vector indicates how quickly the function changes in the direction of steepest ascent, with the direction given by the normalized gradient.
- 📐 The gradient's role in computing directional derivatives and determining the direction of steepest ascent makes it a crucial component in optimization and understanding function behavior.
Q & A
What is the gradient of a multi-variable function?
-The gradient of a multi-variable function is a vector that contains the partial derivatives with respect to each variable. For a function with two inputs, like x and y, the gradient is a vector with the partial derivative with respect to x and the partial derivative with respect to y.
How does the gradient function graphically?
-Graphically, the gradient is represented by a vector field where each vector at a point in the input space (e.g., the x,y plane) points in the direction of the steepest ascent of the function at that point.
What is the direction of steepest ascent?
-The direction of steepest ascent is the direction in which the function increases the most rapidly from a given point. It is indicated by the gradient vector at that point.
How is the direction of steepest ascent related to the gradient?
-The direction of steepest ascent is the direction in which the gradient vector points because the gradient vector indicates the direction of the greatest rate of increase of the function.
What is the role of the directional derivative in understanding the gradient?
-The directional derivative provides a way to quantify the rate of change of the function in a specific direction. It helps in understanding that the gradient vector points in the direction where the directional derivative is maximized.
How do you compute the directional derivative of a function at a point?
-The directional derivative of a function at a point is computed by taking the dot product of the gradient of the function at that point with a unit vector in the direction in which you want to evaluate the rate of change.
Why is the gradient vector considered special in the context of directional derivatives?
-The gradient vector is special because it is the vector that, when used in the directional derivative, gives the maximum rate of change of the function at that point, which is the steepest ascent.
What does the magnitude of the gradient vector represent?
-The magnitude of the gradient vector represents the rate of change of the function in the direction of the gradient itself. It tells you how steep the function is in the direction of the greatest increase.
How do you find the unit vector in the direction of steepest ascent?
-To find the unit vector in the direction of steepest ascent, you take the gradient vector at the point of interest and normalize it by dividing by its magnitude.
What is the relationship between the gradient vector and the rate of change of the function?
-The gradient vector not only points in the direction of the steepest ascent but also its magnitude indicates the rate at which the function changes in that direction.
Can the gradient vector be used to find the direction of steepest descent?
-No, the gradient vector points in the direction of steepest ascent. To find the direction of steepest descent, you would use the negative of the gradient vector.
Outlines
📚 Understanding the Gradient and Directional Derivative
The first paragraph introduces the concept of the gradient of a multi-variable function, using the example of a function f(x, y) = x^2 + y^2. It explains that the gradient is computed by taking the partial derivatives with respect to each variable and that it points in the direction of steepest ascent. The paragraph also introduces the concept of the directional derivative, which measures the rate of change of the function in a specific direction, and explains how the gradient can be used to find the direction of steepest ascent by maximizing the dot product with all possible unit vectors at a given point.
🔍 The Intuition Behind the Gradient's Direction and Magnitude
The second paragraph delves deeper into the intuition behind the gradient's direction and magnitude. It discusses how the dot product between the gradient and a unit vector V can be interpreted as projecting V onto the gradient vector, and how this projection's length is maximized when V is aligned with the gradient. The paragraph emphasizes that the gradient vector, when normalized, points in the direction of steepest ascent and that its magnitude represents the rate of change of the function in that direction, reinforcing the gradient's role as a fundamental tool in multi-variable calculus.
🌟 The Gradient as a Core Concept in Multi-Variable Functions
The third and final paragraph wraps up the discussion by highlighting the gradient's significance in scalar-valued multi-variable functions. It reiterates that the gradient is not only the direction of steepest ascent but also a tool for computing directional derivatives. The paragraph concludes by emphasizing the gradient's magnitude as an indicator of the rate of change in the direction of steepest ascent, solidifying its importance as an extension of the derivative concept in higher dimensions.
Mindmap
Keywords
💡Gradient
💡Partial Derivatives
💡Direction of Steepest Ascent
💡Unit Vector
💡Directional Derivative
💡Dot Product
💡Magnitude
💡Scalar Valued Functions
💡Vector Field
💡Normalization
Highlights
Introduction to the gradient of a multi-variable function with two inputs, such as x squared plus y squared.
Explanation of the gradient as a vector composed of partial derivatives with respect to each input variable.
Graphical intuition of the gradient pointing in the direction of steepest ascent in the input space.
Discussion on the relationship between the gradient and the output space as a number line.
Illustration of the gradient field in the x,y plane for the function f(x squared).
Clarification on the confusion between the combination of partial derivatives and choosing the best direction.
Introduction of the directional derivative as a tool to understand the gradient's role in finding the steepest ascent.
Use of a unit vector to represent a direction in the input space for evaluating the directional derivative.
Explanation of the dot product between the gradient and a unit vector to determine the rate of change in a specific direction.
Insight into maximizing the directional derivative by finding the unit vector that maximizes the dot product with the gradient.
Demonstration of the dot product as a projection of a unit vector onto the gradient vector.
Revelation that the gradient vector itself, when normalized, points in the direction of steepest ascent.
Discussion on the gradient as a tool for computing directional derivatives and its significance.
Interpretation of the gradient's magnitude as the rate of change of the function in the direction of steepest ascent.
Connection between the gradient, its direction, and its magnitude in understanding scalar-valued multi-variable functions.
Highlighting the gradient as an extension of the derivative concept in multi-variable calculus.
Recommendation for further understanding of the dot product through Khan Academy videos for deeper intuition.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: