Stokes' theorem proof part 2 | Multivariable Calculus | Khan Academy

Khan Academy
21 Jun 201207:39
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the concept of parameterizing a surface in a three-dimensional space is explored. The position vector function 'r' is defined with parameters x and y, with the surface's orientation and constraints on the domain of parameters being discussed. The script delves into calculating 'ds', the differential of arc length on the surface, through the cross product of partial derivatives. Emphasis is placed on ensuring the correct orientation of the surface and the accurate computation of the cross product, resulting in a vector pointing perpendicular to the surface.

Takeaways
  • 📐 Parameterization is used to define a surface using a position vector function, which depends on two parameters.
  • 🧮 The parameters can be chosen based on the coordinates of the surface, such as x and y, with z being a function of these parameters.
  • 📏 The domain of the parameters must be defined, indicating which values of x and y are considered.
  • 🔀 The cross product of the partial derivatives of the position vector with respect to the parameters determines the surface's orientation.
  • 📏 The ds element represents the cross product vector scaled by a differential area element da.
  • ✋ The right-hand rule helps determine the correct orientation of the cross product vector for the surface.
  • 🧭 The orientation of the cross product must align with the surface's intended direction, ensuring it points upwards or above the surface.
  • ➕ The calculation of the cross product involves setting up a matrix with i, j, and k unit vectors and the partial derivatives of the components.
  • 📐 The result of the cross product gives a vector that includes components in the i, j, and k directions, corresponding to the surface's orientation.
  • 🔄 The cross product's ordering affects the vector's direction, ensuring the proper orientation of the surface as traversed.
Q & A

  • What is the purpose of parameterizing a surface in mathematics?

    -Parameterizing a surface allows us to describe the surface using a set of parameters, which simplifies the process of calculating properties such as area, volume, and curvature, and makes it easier to work with the surface in equations and computations.

  • Why are x and y chosen as parameters for the surface?

    -X and y are chosen as parameters because they are often the most natural coordinates to describe a surface in a 3D space, especially when the surface can be defined as a function of these variables.

  • What does the position vector function r represent in this context?

    -The position vector function r represents the coordinates of a point on the surface in 3D space as a function of the parameters x and y.

  • What is the significance of the z component in the parameterization of r?

    -The z component in the parameterization of r represents the height or depth of the surface above or below a reference plane, and it is a function of x and y.

  • Why is it important to consider the constraints on the domain for the parameters?

    -Considering the constraints on the domain for the parameters ensures that the parameterization only includes points that are part of the actual surface, preventing the inclusion of points that do not belong to the surface.

  • What does ds represent in the context of the script?

    -In the script, ds represents an infinitesimal element of arc length or area on the surface, which is used in integral calculus to calculate quantities over the surface.

  • How is ds calculated in the script?

    -Ds is calculated as the cross product of the partial derivatives of the position vector function r with respect to each parameter (x and y), which gives a vector that is perpendicular to the surface at that point.

  • What is the significance of the right-hand rule in determining the orientation of the surface?

    -The right-hand rule is used to determine the direction of the cross product, ensuring that the orientation of the surface is consistent with the direction of traversal or the normal vector pointing outward from the surface.

  • Why is the ordering of the cross product important in the parameterization?

    -The ordering of the cross product is important because it determines the direction of the normal vector to the surface, which is crucial for maintaining the correct orientation of the surface in calculations.

  • How is the orientation of the surface ensured to be correct using the cross product?

    -The orientation is ensured by using the right-hand rule and the correct ordering of the cross product components. This ensures that the normal vector points in the direction that is consistent with the traversal of the boundary and the surface's geometry.

  • What is the determinant method used for in the calculation of the cross product in the script?

    -The determinant method is used to calculate the components of the cross product in a systematic way, by using the unit vectors i, j, and k, and the partial derivatives of the position vector function with respect to the parameters.

Outlines
00:00
📚 Parameterization of a Surface

This paragraph introduces the concept of parameterizing a surface in a mathematical context. The speaker defines a position vector function 'r' that depends on two parameters, x and y, to represent the surface. The direction vectors for the parameterization are given as multiples of the unit vectors i and j for x and y, respectively, with z being a function of both x and y. The domain constraints for the parameters are discussed, emphasizing that only certain xy pairs, which are members of a specified region 'r', are considered for defining the surface. The paragraph concludes with the introduction of 'ds', the differential element of the surface area, which is expressed as the cross product of the partial derivatives of the position vector function with respect to x and y, multiplied by a differential area element 'da'. The importance of the correct orientation of the surface is also highlighted.

05:03
🔍 Calculating the Cross Product for Surface Parameterization

The second paragraph delves into the calculation of the cross product necessary for determining the differential element 'ds' of the parameterized surface. The speaker uses the right-hand rule to establish the correct orientation of the surface, ensuring that the cross product points in the direction perpendicular to the surface. The partial derivatives of the position vector with respect to x and y are calculated, resulting in vectors that represent the direction along the surface for each parameter. The cross product is then computed using the determinant of a matrix with the unit vectors i, j, and k, and the partial derivatives of z with respect to x and y. The resulting vector is simplified to -z_x * i - z_y * j + k, which represents the normal vector to the surface, confirming the correct orientation and providing the formula for 'ds' as part of the surface parameterization process.

Mindmap
Keywords
💡Parameterization
Parameterization in the context of the video refers to the mathematical process of defining a surface using two parameters, typically denoted as x and y. It is a fundamental concept in differential geometry and is used to describe the shape and orientation of a surface in a coordinate system. In the script, the position vector function r is defined as a function of x and y, which allows for the representation of the surface in terms of these parameters.
💡Position Vector Function
A position vector function, denoted as r in the script, is a mathematical function that maps each point on a surface to its position in space. It is essential for defining the geometry of the surface and is used to calculate various properties such as gradients and curvature. In the video, r is defined in terms of x, y, and z, where z is a function of x and y, illustrating how the surface is embedded in three-dimensional space.
💡Surface
In the script, a surface is a two-dimensional manifold embedded in a three-dimensional space. It is defined by the position vector function r, which assigns a point in space to each pair of parameters (x, y). The concept of a surface is central to the video's theme, as it is the object being analyzed and parameterized.
💡Domain
The domain in the script refers to the set of all permissible values for the parameters x and y that define the surface. It is the region within which the parameterization is valid and is crucial for understanding the extent and constraints of the surface being studied. The script emphasizes that only pairs of xy-coordinates that are members of this domain are considered part of the surface.
💡Partial Derivative
A partial derivative is a derivative of a function of multiple variables with respect to one of its variables, while the other variables are held constant. In the video, partial derivatives are used to find the rate of change of the position vector function r with respect to x and y, which is essential for determining the orientation and tangent vectors of the surface.
💡Cross Product
The cross product is a binary operation on two vectors in three-dimensional space, resulting in a vector that is perpendicular to the plane containing the original vectors. In the script, the cross product of the partial derivatives with respect to x and y is used to find the differential surface element ds, which represents the orientation of the surface.
💡Differential Surface Element (ds)
The differential surface element, denoted as ds, is a small piece of the surface that can be approximated as a flat area. It is calculated using the cross product of the partial derivatives of the position vector function with respect to the parameters. In the video, ds is used to understand the local geometry of the surface and its orientation.
💡Orientation
Orientation in the script refers to the direction in which the surface is pointing. It is important for understanding how the surface is embedded in space and for ensuring that calculations, such as the cross product, are consistent with the physical interpretation of the surface. The right-hand rule is mentioned to determine the correct orientation of the surface.
💡Right-Hand Rule
The right-hand rule is a common mnemonic used to determine the direction of the cross product of two vectors. It involves aligning the fingers of the right hand to point in the direction of the first vector and then curling them towards the second vector, with the thumb pointing in the direction of the resulting cross product. In the script, this rule is used to confirm the correct orientation of the surface.
💡Determinant
In the context of the script, the determinant is used to calculate the cross product of the partial derivatives in a systematic way. It involves arranging the components of the vectors and the unit vectors i, j, and k into a matrix and then calculating the determinant to find the components of the resulting cross product vector.
💡Unit Vectors (i, j, k)
Unit vectors i, j, and k represent the directions along the x, y, and z axes in a three-dimensional Cartesian coordinate system, respectively. Each has a magnitude of one and is used to express vectors in terms of their components along the coordinate axes. In the script, these unit vectors are used in the calculation of the cross product for the differential surface element.
Highlights

Parameterizing a surface with a position vector function r as a function of two parameters x and y.

Defining the parameterization in the i, j, and k directions with x times i, y times j, and z as a function of x and y.

Considering constraints on the domain for the parameters, ensuring xy pairs are members of the defined region.

Only considering the z of xy pairs where xy is part of the region to define the surface.

Exploring the concept of ds for a parameterized surface and its relation to the cross product of partial derivatives.

Using the right-hand rule to determine the correct orientation of the surface based on the parameterization.

Ensuring the cross product points in the right direction for proper surface orientation during boundary traversal.

Calculating the cross product of the partial derivatives with respect to x and y to find ds.

Using the determinant of a matrix with i, j, k unit vectors to represent the cross product.

Deriving the components of the cross product by considering the partial derivatives of the i, j, and k components.

Finding the i component of the cross product by taking the determinant of the partial derivatives.

Calculating the j and k components of the cross product using the determinant method.

Arriving at the final expression for the cross product as -z_x times i - z_y times j + k.

Highlighting the importance of careful parameterization to ensure correct surface orientation.

Demonstrating the process of calculating ds for a parameterized surface through a step-by-step approach.

Using the right-hand rule to visually confirm the correct orientation of the cross product vector.

Providing a comprehensive explanation of the mathematical concepts involved in parameterizing and differentiating surfaces.

Transcripts

Browse More Related Video

Divergence theorem proof (part 3) | Divergence theorem | Multivariable Calculus | Khan Academy

Constructing a unit normal vector to a surface | Multivariable Calculus | Khan Academy

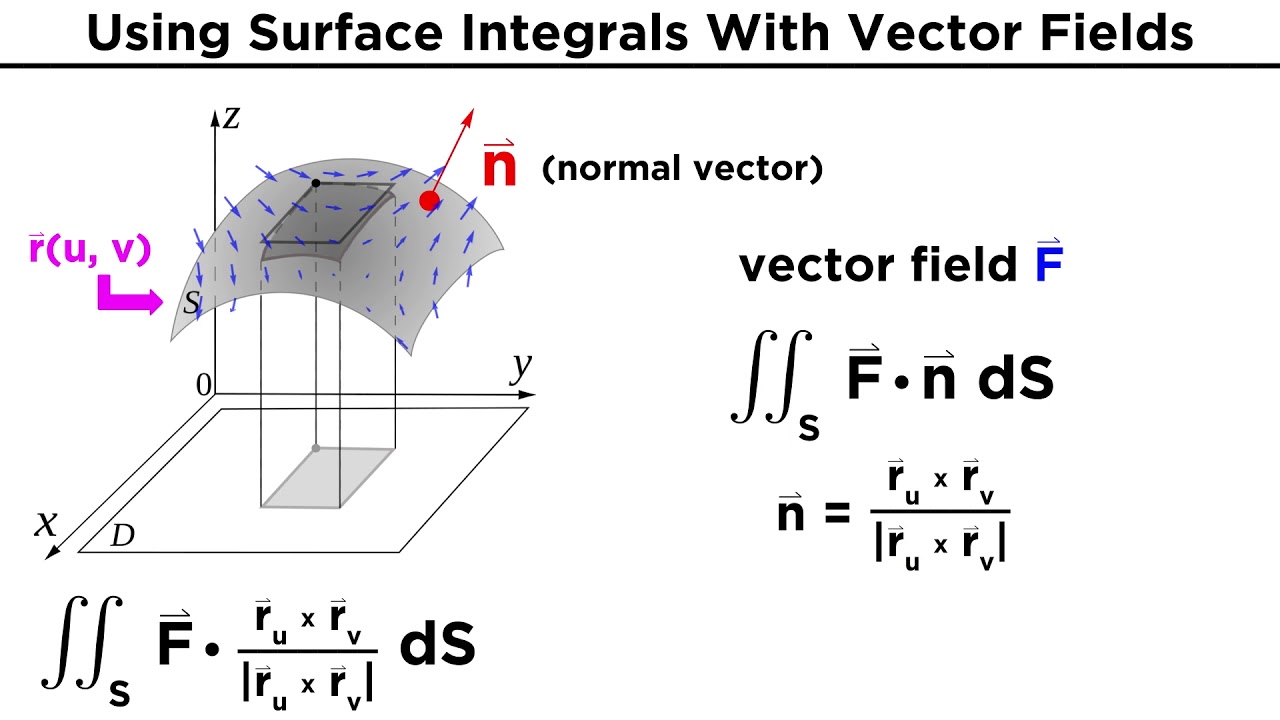
Evaluating Surface Integrals

Surface integral ex3 part 3: Top surface | Multivariable Calculus | Khan Academy

Example of calculating a surface integral part 1 | Multivariable Calculus | Khan Academy

Stokes example part 3: Surface to double integral | Multivariable Calculus | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Surface ParameterizationDifferential GeometryCross ProductPartial DerivativesVector AnalysisMathematics TutorialSurface OrientationDomain ConstraintsParameter ConstraintsRight-Hand RuleDeterminant Method